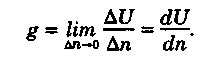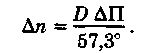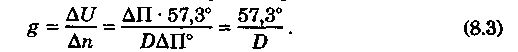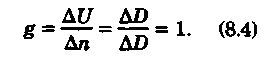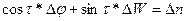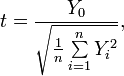градиент расстояния чему равен

(32)

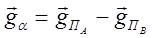
Модули градиентов соответствующих пеленгов выразятся равенствами g₁=g_ПА = 1/D_А; g₂=g_ПВ = 1/D_В.

Найденные абсолютные значения градиентов определяют длины двух сторон векторного треугольника. Вычислим третью сторону по формуле косинуса угла плоского треугольника:

(33)

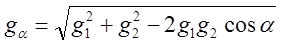
Раскрыв значения модулей градиентов и приведя к общему знаменателю, получим

(34)

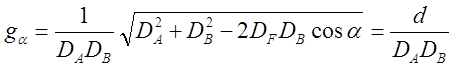
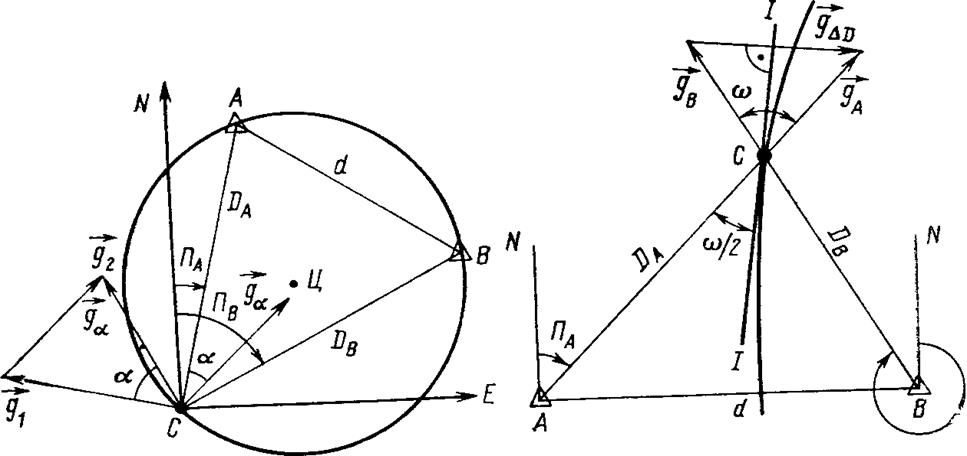
Рис. 14. Градиент горизонтального угла Рис. 15. Градиент разности растояний

, (36)

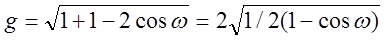
где w — угол между направлениями на ориентиры в счислимой точке С, часто называемый базовым.

Применяя формулу разложения квадратов тригонометричес­ких функций по кратным дугам, получим

Формулы (37) и (38) справедливы для плоскости и для сферической гиперболы. Этот вывод вытекает из равенства единице модулю градиента сферического расстояния и того факта, что касательная к сферической гиперболе делит базовый угол w пополам так же, как и в плоской гипер­боле.

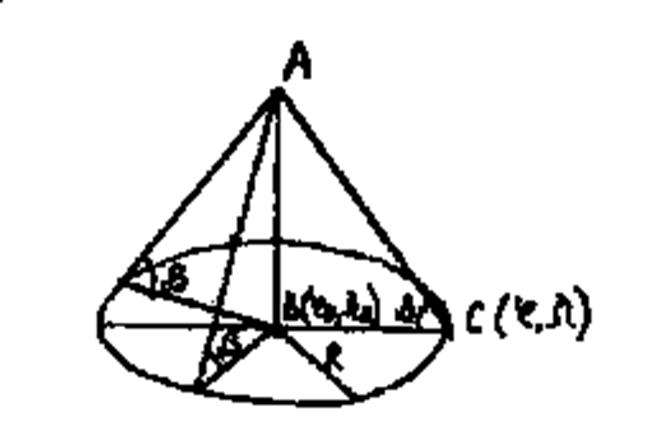
Градиент вертикального угла

(39)

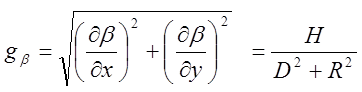
Рис. 16. Градиент вертикального угла

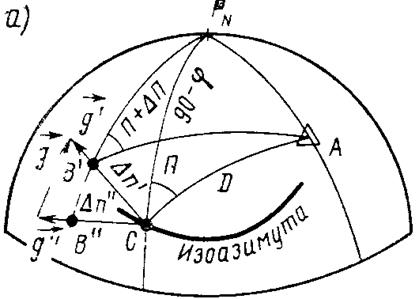
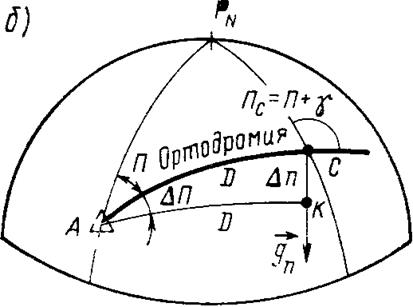
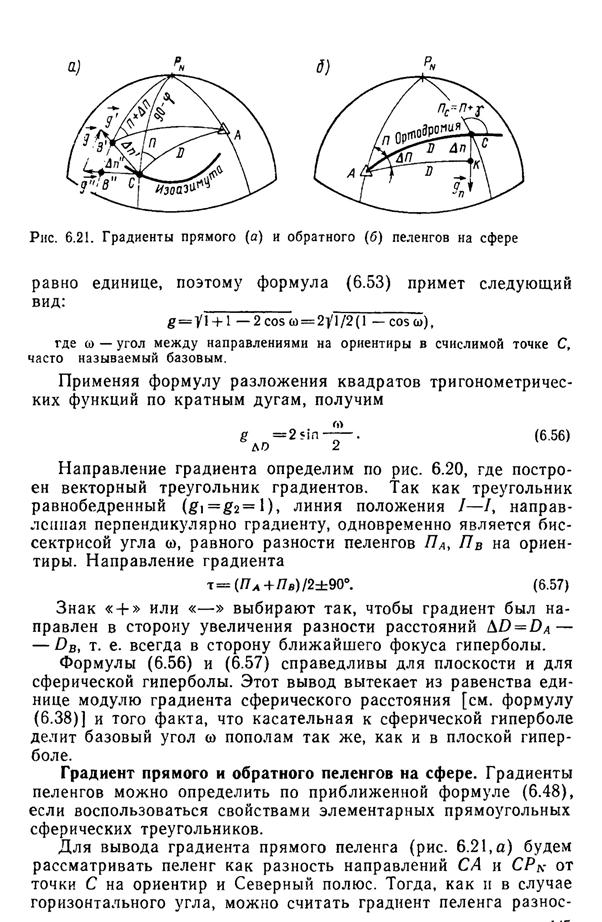
Рис. 17. Градиенты прямого (а) и обратного (б) пеленгов на сфере

Градиент прямого и обратного пеленгов на сфере. Градиенты пеленгов можно определить по приближенной формуле (25), если воспользоваться свойствами элементарных прямоугольных сферических треугольников.

Для вывода градиента прямого пеленга (рис. 17, а) будем рассматривать пеленг как разность направлений СА и СP_N от точки С на ориентир и Северный полюс. Тогда, как и в случае горизонтального угла, можно считать градиент пеленга разностью градиентов направлений СА и СP_N.

Применяя формулу косинуса стороны для плоского треу­гольника, образованного длинами градиентов, получим оконча­тельную формулу модуля градиента прямого пеленга на сфере

(41)

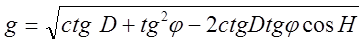
Зная теперь длины всех сторон треугольника градиентов и его ориентацию относительно меридиана, по формулам плоской тригонометрии можно вывести выражение для направления гра­диента пеленга

Если пеленг измерен в не слишком высоких широтах j и на малых расстояниях D, то допустимы следующие упрощения:

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Изолинии и градиенты расстояния, пеленга, горизонтального угла, разности расстояний. Линия положения и ее элементы. Способы построения линий положения.

Измеряемые для определения места судна направления и расстояния или их производные (углы, разность расстояний) до объектов с известными координатами называются навигационными параметрами. Геометрическое место точек, отвечающее постоянному значению навигационного параметра, называется навигационной изолинией. Любые измерения содержат ошибки, поэтому измерив пеленг, дистанцию или угол и проложив на карте соответствующую изолинию, нельзя считать, что судно будет находиться на этой изолинии. Вычислить возможное смещение изолинии из-за ошибок наблюдений можно, используя понятие ГРАДИЕНТА ФУНКЦИИ.

На всей изолинии значение функции навигационного параметра остается постоянным, но оно изменится при переходе на другую изолинию. Чем теснее расположены изолинии друг к другу, тем меньше расстояние An между ними при заданном приращении функции AU, тем быстрее меняется функция в данном районе. Это изменение удобно характеризовать отношением AU/n или вектором g, направленным в сторону возрастания функции по нормали к изолинии. Вектор g называется градиентом. Таким образом, градиентом навигационного параметра называется вектор, направленный по нормали к навигационной изолинии в сторону ее смещения при положительном приращении параметра, причем модуль этого вектора характеризует наибольшую скорость изменения параметра в данном месте Этот модуль равен

Направления вектора градиента и линии положения взаимно перпендикулярны, обозначается направление градиента символом т.

Если при измерении навигационного параметра U допущена ошибка AU и известен градиент, то смещение линии положения параллельно самой себе определяется формулой

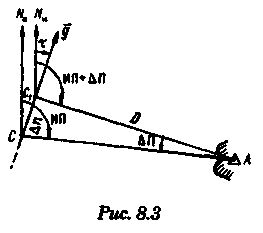
Пеленг. Предположим, что наблюдатель, находившийся в точке С, переместился так, что пеленг получил приращение An, град. (рис. 8.3). Следовательно, AU = An. Из треугольника АСС> имеем

Значение модуля градиента тогда равно, град, /миля, AU

РАССТОЯНИЕ:При измнрении расстояния дU=дD, смещение изолинии дn=дDзначит

Смещение линии положения, полученной по измеренному расстоянию, зависит только от ошибки в измеренном расстоянии.

ГОРИЗ. УГОЛ Значение модуля градиента можно получить, предварительно вычислив значение градиента функции, если рассмотреть угол как разность двух направлений (пеленгов) и использовать теорему о том, что градиент разности двух функций равен геометрической разности градиентов этих функций

Дата добавления: 2015-04-18 ; просмотров: 119 ; Нарушение авторских прав

Источник

Градиент навигационного параметра

Любые измерения содержат ошибки, поэтому измерив пеленг, дистанцию или угол и проложив на карте соответствующую изоли­нию, нельзя считать, что судно будет находиться на этой изолинии. Вычислить возможное смещение изолинии из-за ошибок наблюдений можно, используя понятие градиента функции.

Изобразим две изолинии, соответствующие значениям навигацион­ных параметров U и U + ∆U (рис. 8.2). На всей изолинии значение функции навигационного параметра остается постоянным, но оно изме­нится при переходе на другую изолинию. Чем теснее расположены изо­линии друг к другу, тем меньше расстояние ∆n между ними при задан­ном приращении функции ∆U, тем быстрее меняется функция в данном районе. Это изменение удобно характеризовать отношением ∆U/∆n или вектором g, направленным в сторону возрас­тания функции по нормали к изолинии. Век­тор g называется градиентом. Таким образом, градиентом навигационного параметра назы­вается вектор, направленный по нормали к навигационной изолинии в сторону ее смеще­ния при положительном приращении пара­метра, причем модуль этого вектора характе­ризует наибольшую скорость изменения па­раметра в данном месте. Этот модуль равен

Размерность модуля градиента равна размерности параметра U на линейную величину. Направления вектора градиента и линии положения взаимно перпендикулярны, обозначается направление градиента символом r.

Если при измерении навигационного параметра U допущена ошибка ∆U и известен градиент, то смещение линии положения па­раллельно самой себе определяется формулой

Чем больше величина градиента g, тем меньше смещение линии положения при той же ошибке ∆U, тем точнее будет определение места судна.

Значение модуля градиента тогда равно, град, /миля,

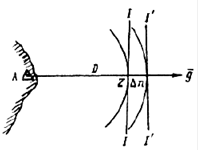
Расстояние. При измерении рас­стояния ∆U = ∆D, смещение изолинии
∆n = ∆D.

будет совпадать с направлением из ориентира А на точку Z, в которой находится судно (рис. 8.4). Смеще­ние линии положения, полученной по измеренному расстоянию, зави­сит только от 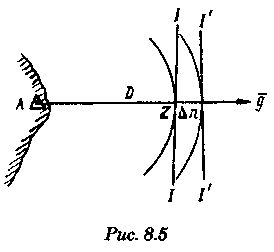ошибки в измеренном расстоянии.

23)Линия положения. Уравнение линии положения.

Линией положения называется касательная (или хорда), проведенная к изолинии вблизи счислимого места и замещающая собой изолинию.

24)Способы ОМС по двум линиям положения.

25)Градиенты навигационного параметра.

26)Основные понятия и определения теории вероятности. Законы распределения случайных величин.

Частное определение: отношение числа случаев появления события A(m) к общему числу проведённых испытаний (n)

Классическое определение: отношение числа испытаний благоприятных событию A(m) к общему числу испытаний (n)

Косвенное определение вероятности: в этом случае сложные события разбиваются на несколько простых, вероятность которых подсчитывается частными или классическими, затем вероятность сложного события определяется по вероятностям составляющих его простых событий с использованием теорем сложения и умножения вероятностей.

Случайные величины и законы их распределения (СВ)

Дискретные: происходят через определённый интервал времени.

Непрерывные: непрерывные события.

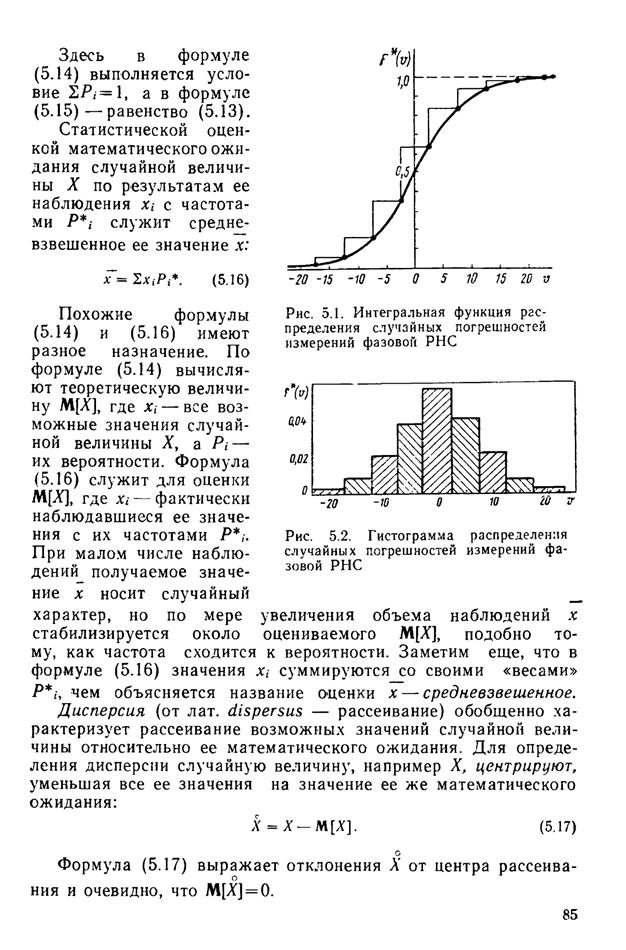
Самый распространенный и наиболее общим законом распределения случайной величины при неограниченном количестве измерений наз-ся закон Гаусса.

27)Числовые характеристики случайных величин и случайных функций.

28)Измерения и наблюдения. Классификация измерения.

Дискретные – это такие измерения которые выполняются через определённый интервал времени.

Непрерывные – это те измерения которые ведутся всегда автоматизированными аппаратами.

Необходимые – это измерения минимальное количество которых обеспечивает….

Избыточные – это такие которые выполнены сверх необходимых.

Равноточные – это такие СКП результат измерения которых будет одинаковый.

По степени взаимо связи:

1) взаимонезависимы – измерение погрешности которой формируется различными факторами.

2) корреляционновзаимозависимы – это измерения в состав погрешности которых входит одна и та же общая погрешность сформирована одним и тем же фактором.

3) Функциональнозависимы – это измерения все погрешности которых формируются одним и тем же фактором.

29)Классификация погрешности и их свойства. Методы учёта систематических погрешностей.

Погрешность измерения называется разница между измеренным и истинным значением величины.

Непосредственно источник погрешности является.

По характеру действия на величину погрешности подразделяются на:

30. Нормальный закон распределения погрешностей и функцию Лапласа спотреть в 25. Распределение Стьюдента

Распределе́ние Стью́дента в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений. Названо в честь Уильяма Сили Госсета, который первым опубликовал работы, посвящённые распределению, под псевдонимом «Стьюдент».

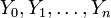
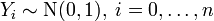
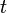
Пусть — независимые стандартные нормальные случайные величины, такие что . Тогда распределение случайной величины , где

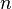
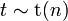
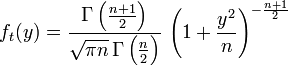
называется распределением Стьюдента с степенями свободы. Пишут . Её распределение абсолютно непрерывно и имеет плотность

,

где 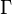— гамма-функция Эйлера.

Источник

Навигационный параметр, градиент навигационного параметра, навигационная изолиния, линия положения, полоса положения.

Навигационным параметром называют физическую величину, которая известным образом зависит от положения судна относительно ориентиров и измеряется для определения места судна.

Примеры параметров: расстояние до ориентира D, высота светила h, пеленг ориентира П, разность расстояний DD и т. п.

Градиент навигационного параметра – это вектор g направленный перпендикулярно к изолинии в сторону увеличения навигационного параметра. Вектор этого модуля характеризует наибольшую скорость изменения в данном месте, причем:

,

где — навигационный параметр;

— линейное смещение навигационной изолинии.

Для определения градиентов вместо точного равенства пользуется приближенным выражением:

,

где — малое приращение навигационного параметра;

— смещение навигационной изолинии.

градиент высоты светила равен градиенту дистанции ;

градиент пеленга ; , поэтому .

Геометрическое место точек, отвечающее постоянному значению навигационного параметра, называется навигационной изолинией. В навигации для определения места судна используются следующие навигационные параметры и соответствующие им изолинии:

Пеленг. На судне измерен истинный пеленг (ИП) предмета А, равный a. Проложив на карте линию пеленга АД, можно увтерждать, что судно в момент взятия пеленга находилось на этой линии. Прямая линия АД, отвечающая условию задачи, на которой находилось судно в момент наблюдения, будет называться изолинией пеленга или изопеленгой.

Расстояние. Измерено расстояние Д между судном и ориентиром А. В этом случае судно будет находится на окружности радиусом Д с центром в точке А. Эта окружность будет называться изолинией расстояния или изостадией.

Горизонтальный угол. Если измерен горизонтальный угол между ориентирами А и Б, равный a, или этот угол вычислен как разность двух пеленгов . Эта окружность называется изолинией горизонтального угла или изогоной.

Разность расстояний. В некоторых радионавигационных системах измеряется разность расстояний до двух ориентиров. Тогда изолинией разности расстояний будет гипербола.

Линией положения называется прямая, заменяющая небольшой участок навигационной изолинии вблизи счислимого места судна. Это определение в первую очередь имеет в виду касательную к изолинии.

При воздействии случайных погрешностей измерений смещение каждой линии положения характеризуется линейной величиной , в результате чего образуется полоса положения. Если смещение равно среднему квадратическому отклонению , то полоса положения

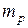
Погрешность определения места, являющаяся результатом случайных погрешностей в двух линиях положения, характеризуется площадью параллелограмма, образованным двумя параметрами и .

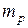
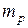
Вероятность нахождения судна в площади параллелограмма около 50%; если взять для расчёта 2 , то вероятность увеличивается до 95%, а если принять предельную ошибку 3 , то вероятность повышается до 99%.

Для удобства анализа точность обсервации места судна целесообразнее оценить не площадью, а одним числом. За среднюю квадратическую ошибку обсервованного места М принимают радиус круга, охватывающий эллипс погрешности. Этот радиус равен:

.

Вероятность того, что место судна находится внутри радиуса круга М изменяется от 63,2 до 68,3% и зависит от соотношения полуосей a и b.

18. Опознавание различных береговых ориентиров и средств навигации в дневное и ночное время. Дальность открытия маяка.

Средства навигационного оборудования.

Опасные в навигационном отношении места как в открытом море, так и вблизи берегов ограждаются соответствующими знаками или сооружениями, которые называются средствами навигационного оборудования.

Средства навигационного оборудования подразделяются на береговые и плавучие.

Береговые СНО.

К береговым СНО относятся маяки, навигационные и створные знаки.

Маяк представляет собой фундаментальное строение башенного типа, оборудованное в верхней части специальным световым аппаратом. Маяк не только предупреждает об опасности, но и служит для определения места судна в море. Для того чтобы мореплаватель мог опознать маяки, их строят различной приметной формы и придают огню каждого маяка особую световую характеристику. Это помогает судоводителю безошибочно определить местонахождение своего судна (в том случае, если он детально изучил предстоящий район плавания).

Отличительной характеристикой маяка являются: характер и цвет огня; число проблесков или затмений; период проблесков; Дальность видимости маяка в милях на картах и пособиях приведена для высоты глаза наблюдателя в 5 м; указывается обслуживаемый маяк пли нет; сведения о техническом вооружении маяка; сведения об имеющихся лоцманских и спасательных станциях и средствах связи.

Для обеспечения безопасности плавания во время тумана и ограниченной видимости на маяках подают звуковые сигналы при помощи сирены, тифона, наутфона, колокола, предупреждающие судоводителя о близкой навигационной опасности. На картах маяки обозначаются звездочками с просветом посередине и с точкой в центре, указывающей точное положение маяка на карте. На генеральных картах все маячные огни независимо от их цвета изображаются желтыми пятнами. Около условного изображения маяка на карте ставится его полная характеристика и название. Если маяк светит только в определенном секторе, то этот сектор наносится в виде пунктира. Например, рядом с обозначением маяка на карте стоит надпись ГР Пр (2) (20с) 18м Т (с) РМк ЛС. Расшифровывается это так: маяк имеет огонь группо-проблесковый, 2 проблеска в группе, продолжительность периода 20 секунд, дальность видимости огня 18 миль, туманный сигнал — сирена, имеются радиомаяк и лоцманская станция.

Рис. 33. Береговые створные знаки

.Навигационные знаки — специальные сооружения различной конструкции, по размерам значительно меньше маяков. Они могут быть освещаемыми и неосвещаемыми. Включение огня на знаках производится обычно автоматически при помощи фотоэлементов. Знаки постоянно не обслуживаются. Освещаемые навигационные знаки имеют отличительную от других знаков района световую характеристику, которая, как правило, бывает проблесковой, постоянной или группо-проблесковой. Кроме того, освещаемые знаки различаются по цвету огня. Само расположение знака и характеристика его огня наносятся на навигационную карту. Дальность видимости огней таких знаков достигает 6—8 миль при ясном состоянии атмосферы.

Створные знаки устанавливаются на берегу для указания судового хода на фарватерах и в узкостях (рис. 33). Они служат для обеспечения безопасности прохода судов в районах со стесненными условиями плавания. Кроме того, створные знаки устанавливаются при оборудовании мерных линий Знаки бывают деревянными, металлическими, каменными, освещаемыми и неосвещаемыми. Днем на белых (черных) трапециевидных щитах отчетливо видны черные (белые) вертикальные полосы, а ночью в верхней части щитов зажигаются огни, чаще всего красного или зеленого цвета, чтобы их легко было отличить от любых случайных огней населенного берегового пункта. Направление линий створов на фарватере, узкости или мерной линии нанесено па навигационной карте. На карту мелкого масштаба нельзя одновременно нанести два створных знака, тогда наносят один знак и линию, а рядом ставят пояснительную надпись «2 ств. зн. ».

Линия девиационных, ограничительных и поворотных створов на карте обозначается точечным пунктиром, а ходовые направления— сплошной линией. Значения направления створов даются на карте только истинные.

Источник