грань у куба что это

Грань у куба что это

Куб или правильный гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы.

В различных дисциплинах используются значения термина, имеющие отношения к тем или иным свойствам геометрического прототипа. В частности, в аналитике (OLAP-анализ) применяются так называемые аналитические многомерные кубы, позволяющие в наглядном виде сопоставить данные из различных таблиц.

Содержание

Свойства куба

Диагональю куба называют отрезок, соединяющий две вершины, симметричные относительно центра куба. Диагональ куба находится по формуле , где d — диагональ, а — ребро куба.

Тела кубической формы

В микромире

Примечания

См. также

Полезное

Смотреть что такое «Куб» в других словарях:

куб — куб, а, мн. ч. к уб ы, к уб ов … Русский орфографический словарь

куб — 1. КУБ, а; кубы; м. [греч. kybos] 1. Геометрическое тело правильный шестигранник, все грани которого квадраты; предмет, имеющий форму такого шестигранника. Начертить куб. Композиция из гипсовых кубов и призм. Мраморный куб памятника. 2. Разг. =… … Энциклопедический словарь

КУБ — ОАО АКБ «Кузбассугольбанк» http://cbank.ru/​ организация, фин., энерг. КУБ кнопочный пост управления взрывобезопасный КУБ ОАО «Кредит Урал банк» http://www.credit … Словарь сокращений и аббревиатур

куб — сущ., м., употр. сравн. часто Морфология: (нет) чего? куба, чему? кубу, (вижу) что? куб, чем? кубом, о чём? о кубе; мн. что? кубы и кубы, (нет) чего? кубов и кубов, чему? кубам и кубам, (вижу) что? кубы и кубы, чем? кубами и кубами, о чём? о… … Толковый словарь Дмитриева

кубіт — кубі/т, род. кубіта, мн. кубіти, род. мн. кубітів одиниця інформації, що закодована в квантовій системі, фізичний носій інформації, що може перебуватив станах |0> та |1> і будь якій суперпозиції цих станів. • Стан кубіта може змінюватись… … Фізико-технічний словник-мінімум

КУБ — 1. КУБ1, куба, муж. (греч. kybos). 1. Правильный шестигранник, все грани которого (квадраты (мат.). Начертить куб. 2. Мера объема, равная кубическому метру. Куб дров. 3. Сосуд для перегонки или кипячения жилкостей в форме шара или цилиндра с… … Толковый словарь Ушакова

КУБ — 1. КУБ1, куба, муж. (греч. kybos). 1. Правильный шестигранник, все грани которого (квадраты (мат.). Начертить куб. 2. Мера объема, равная кубическому метру. Куб дров. 3. Сосуд для перегонки или кипячения жилкостей в форме шара или цилиндра с… … Толковый словарь Ушакова

КУБ — (от латинского cubus, от греческого kybos игральная кость), 1) один из 5 типов правильных многогранников, имеющий гранями квадраты, 12 ребер, 8 вершин, в каждой вершине сходятся 3 ребра. Куб иногда называют гексаэдром. 2) Третья степень а3 числа… … Современная энциклопедия

КУБ — КУБ, в математике результат двукратного умножения числа на самого себя. Таким образом, кубом числа а является произведение а х а х а, что записывается как а3. Куб называют также третьей степенью числа. Кубом именуется правильная шестисторонняя… … Научно-технический энциклопедический словарь

Источник

Куб (геометрия)

Куб (геометрия)

Куб
Тип	Правильный многогранник
Грань	квадрат
Вершин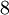
Рёбер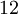
Граней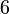
Граней при вершине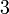
Длина ребра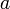
Площадь поверхности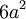
Объём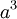
Радиус вписаной сферы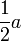
Радиус описаной сферы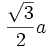
Угол наклона грани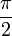
Угол наклона ребра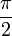
Точечная группа симметрии	Октаэдрическая (Oh)
Двойственный многогранник	Октаэдр

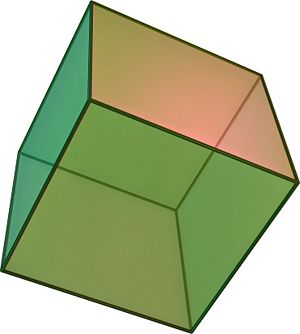
Куб или гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы.

Содержание

Свойства куба

Тела кубической формы

В микромире

Примечания

См. также

Ссылки

Трёхмерные (Тетраэдр • Куб • Октаэдр • Додекаэдр • Икосаэдр)
Четырёхмерные (6 правильных многогранников)
Большей размерности
(только 3 типа правильных многогранников: n-мерный симплекс, n-мерный октаэдр, n-мерный куб)

Звёздчатый многогранник
(Звёздчатый октаэдр, Звёздчатый додекаэдр, Звёздчатый икосаэдр, Звёздчатый икосододекаэдр)

Полезное

Смотреть что такое «Куб (геометрия)» в других словарях:

ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера

МНОГОМЕРНАЯ ГЕОМЕТРИЯ — геометрия пространств размерности, большей трех; термин применяется к тем пространствам, геометрия к рых была первоначально развита для случая трех измерений и только потом обобщена на число измерений n>3, прежде всего евклидово пространство,… … Математическая энциклопедия

N-мерная евклидова геометрия — N мерная евклидова геометрия обобщение евклидовой геометрии на пространство большего числа измерений. Хотя физическое пространство является трёхмерным[1], и человеческие органы чувств рассчитаны на восприятие трёх измерений[2], N мерная… … Википедия

Пирамида (геометрия) — У этого термина существуют и другие значения, см. Пирамидацу (значения). Достоверность этого раздела статьи поставлена под сомнение. Необходимо проверить точность фактов, изложенных в этом разделе. На странице обcуждения могут быть пояснения … Википедия

Конструктивная блочная геометрия — (Constructive Solid Geometry, CSG) технология, используемая в моделировании твёрдых тел. Конструктивная блочная геометрия зачастую, но не всегда, является способом моделирования в трёхмерной графике и САПР. Она позволяет создать сложную сцену или … Википедия

Координационная геометрия — Содержание 1 Молекулы 2 Координационные комплексы неорганических соединений … Википедия

Конструктивная сплошная геометрия — Конструктивная блочная геометрия (Constructive Solid Geometry, CSG) технология, используемая в моделировании твёрдых тел. Конструктивная блочная геометрия зачастую, но не всегда, является способом моделирования в трёхмерной графике и САПР. Она… … Википедия

Призма (геометрия) — У этого термина существуют и другие значения, см. Призма … Википедия

Объём (геометрия) — У этого термина существуют и другие значения, см. Объём (значения). Объём это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого… … Википедия

Объем (геометрия) — Объём это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого определения в отношении трёхмерных тел трёхмерного евклидова пространства.… … Википедия

Источник

Грань у куба что это

Куб – правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны.

Свойства куба:

2. Противоположные грани попарно параллельны.

3. Все двугранные углы куба – прямые.

Прямоугольный параллелепипед

Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

1. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.

Чтобы были понятны формулы, введем обозначения:

$с$-высота(она же боковое ребро);

$S_<п.п>$-площадь полной поверхности;

$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.

Пирамида

Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.

Формулы вычисления объема и площади поверхности правильной пирамиды.

В основании лежат правильные многоугольники, рассмотрим их площади:

Задачи на нахождение объема составного многогранника:

Задачи на нахождение площади поверхности составного многогранника.

— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:

Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.

— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.

Источник

Куб и его свойства

Урок 5. Наглядная геометрия 5–6 классы ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Куб и его свойства»

На одном из предыдущих занятий мы с вами познакомились с таким многогранником, как прямоугольный параллелепипед.

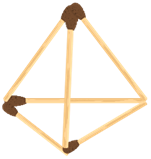
Решая задачу со спичками, получили геометрическую фигуру, которую называют пирамидой.

Впереди вас ожидает знакомство и с другими многогранниками. А сейчас давайте вернёмся к прямоугольному параллелепипеду.

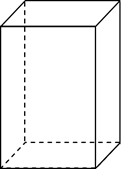
Итак, поверхность прямоугольного параллелепипеда состоит из 6 прямоугольников. Эти прямоугольники называются гранями параллелепипеда.

Обратите внимание, что два соседних прямоугольника имеют общую сторону, которая называется ребром прямоугольного параллелепипеда. Концы рёбер называются вершинами прямоугольного параллелепипеда.

Таким образом, прямоугольный параллелепипед имеет 6 граней, 12 рёбер и 8 вершин.

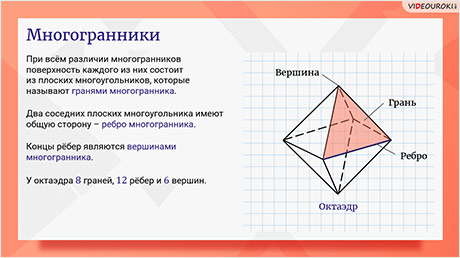
Отметим, что при всём различии многогранников поверхность каждого из них состоит из плоских многоугольников, которые называют гранями многогранника. Два соседних плоских многоугольника имеют общую сторону – ребро многогранника. Концы рёбер являются вершинами многогранника.

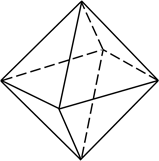
Этот многогранник называется октаэдром. У него 8 граней, которые являются треугольниками, 12 рёбер и 6 вершин.

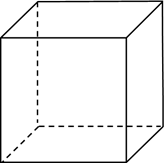
Куб – это такой прямоугольный параллелепипед, в котором все рёбра равны между собой. Обратите внимание, что рёбра куба, которые не видны, мы изображаем пунктирными линиями. Это позволяет получить полное представление о фигуре и её расположении по отношению к нам.

Все грани куба – равные между собой квадраты. Поверхность куба состоит из 6 равных квадратов. Посмотрите, что грани, расположенные друг против друга, не имеют общих рёбер. Эти грани называются противоположными.

Грани, которые имеют общее ребро, называются смежными.

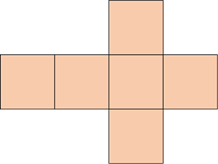
А теперь давайте проведём небольшой эксперимент. Возьмём коробку, которая имеет форму куба. Откроем её, потом разрежем по четырём вертикальным рёбрам, а затем развернём.

Фигуру, которая у нас получилась, называют развёрткой куба. Она состоит из 6 равных квадратов.

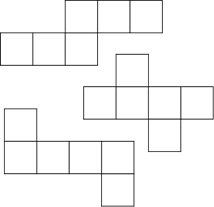
Следующие фигуры также являются развёртками куба.

С помощью любой из развёрток вы можете изготовить модель куба. Для этого можно поступить следующим образом. Начертить на листе бумаги развёртку куба. Вырезать её. Согнуть по отрезкам, которые соответствуют рёбрам куба, и склеить.

Теперь давайте проведём с вами отрезок, который соединит наиболее удалённые друг от друга вершины куба. Эти вершины называют противоположными.

Отрезок, соединяющий две противоположные вершины куба, называется диагональю куба.

А теперь давайте с вами решим несколько задач.

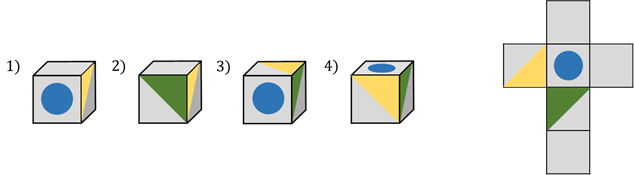
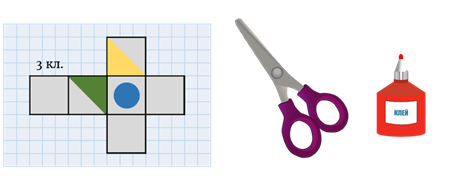
Задача первая. Определите, какой кубик получится из данной развёртки.

Давайте мысленно представим, какие грани кубика являются смежными, то есть имеют общее ребро, и сравним с предложенными вариантами, чтобы найти верный. Для этого нам удобнее всего сравнивать грани, которые отличаются по нанесённому на них рисунку. Обратите внимание на грань с жёлтым треугольником и грань с зелёным треугольником. Очевидно, что эти грани будут смежными при сборке кубика. При этом возможны четыре варианта взаимного расположения этих граней при различных поворотах кубика.

Теперь сравним с четырьмя предложенными вариантами. Сразу видим, что вариант первый неверный. Вариант второй неверный. Очевидно, что вариант третий тоже неверный. А вот вариант четвёртый верный, так как грани, на которых изображены треугольники, расположены верно. При этом на верхней грани должен быть изображён синий круг. Действительно так.

Таким образом, мы с вами выяснили, что из данной развёртки получится куб под номером 4.

Данную задачу вы можете решить ещё одним способом. А именно нарисовать данную развёртку на бумаге. Причём удобнее это сделать на листочке в клеточку, тогда вам не надо будет использовать линейку, чтобы соблюдать размеры кубика. Вы просто будете отсчитывать нужное количество клеточек.

Затем нужно будет раскрасить нарисованную развёртку и вырезать. Потом свернуть из неё куб и склеить его. После чего вы легко можете сравнить получившийся куб с каждым из предложенных вариантов и выбрать верный.

Задача вторая. Модель куба с длиной ребра 4 сантиметра окрасили в серую краску и распилили вдоль рёбер на кубики с длиной ребра 1 см. Сколько среди полученных кубиков: а) окрашенных с трёх сторон; б) окрашенных с двух сторон?

Задача третья. На рисунке изображён каркас куба. Проведите видимые рёбра так, чтобы куб был «виден»: а) сверху слева; б) снизу справа.

Задача четвёртая. На рисунке изображена фигура, сложенная из пяти кубиков. Какой вид будет иметь данная фигура, если смотреть на неё: а) спереди; б) слева; в) сверху?

Источник

Урок математики в 3-м классе «Куб. Элементы куба: грани, ребра, вершины. Развертка куба»

1. Организационный момент.

2. Актуализация опорных знаний

Появляется на экране мультимедийная презентация.

Рассмотрите геометрические фигуры. В них записаны математические выражения. Вычислите значение числового выражения, которое находится:

а) на пересечении круга и прямоугольника?

— Какое правило применили? (Деление числа на произведение)

в) Выражение, которое находится на пересечении квадрата и прямоугольника?

г) Выражение, которое находится в левом полукруге?

— Каким правилом пользовались?

(Умножение числа на произведение)

д) Выражение, которое содержится в ромбе, но не содержится в квадрате.

8 дм 4 см * 3= 84 см *3= 252см= 25 дм 2 см

— У каких этих фигур мы можем найти периметр?

— У каких фигур можем определить периметр несколькими способами?

На экране появляются слайд с формулами.

— Как найти периметр квадрата?

— А как найти площадь у прямоугольника?

— Как найти площадь у квадрата?

Обобщение: Вы хорошо знаете геометрические фигуры и вычисляете выражения. Знаете правила нахождения площади и периметра. Это нам необходимо для решения задач.

3. Постановка учебной задачи.

— Что общего у этих фигур (Плоские)

— Какие еще могут быть фигуры, кроме плоских? (Объемные)

— С каким геометрическим телом уже знакомы? (Параллелепипедом)

4. Закрепление изученного

А сейчас решим задачу из учебника.

— Можем сразу найти площадь квадрата? (Нет)

— Почему? (Не знаем сторону квадрата)

— Как узнать? ( 36:4=9 мм)

— Какой формулой мы будем пользоваться для нахождения площади квадрата?

— Решим эту задачу с комментированием?

— Начертите этот квадрат.

— Что вы знаете о прямоугольнике?

*Противоположные стороны равны.

*Диагонали прямоугольника равны.

*Диагонали прямоугольника пересекаются и точкой пересечения делятся пополам.

— Решите задачу следующую задачу.

— Можем сразу ответить на вопрос? (Да)

— Как? ( площадь разделить на ширину)

Д/в. Что вы знаете о квадрате?

*Диагонали квадрата равны.

*Диагонали пересекаются и точкой пересечения делятся пополам.

*Диагонали квадрата пересекаются под прямым углом.

— Составьте обратные задачи данной.

5. Самостоятельная работа

— Можем сразу ответить на требование задачи? (Да)

— Как? (площадь разделить на длину)

— Эту задачу решит 1 вариант.

Кто выполнит задачу, решит дополнительно. Задание по своим силам, по выбору?

— Составим вторую задачу.

Длина участка прямоугольной формы 86 метров, ширина 40 м. Найдите площадь участка?

— Какой формулой будем пользоваться?( S квадрата = a * b)

— Дополнительно решите еще карточку по выбору

На каждой парте лежат дифференцированные задания.

Проверка самостоятельной работы.

В момент ответа учеников на экране появляются названные фигуры.

— Что такое трапеция?

*Это четырехугольник, у которого параллельны только 2 стороны.

— Что такое параллелограмм?

* Это четырехугольник, у которого все противоположные стороны равны и параллельны.

6. Физминутка.

Немного отдохнем, поработаем устно с геопланами. (У каждого ученика на парте) Нужно узнать фигуру по описанию. Прежде, чем начнем работать, используя таблицу, оцените свои знания, выберите круг нужного цвета. Будьте внимательны, мы учимся самоконтролю!

(На экране появляется таблица )

(Один ученик работает на магнитной доске, остальные с геопланами)

Проверка на магнитной доске

— Какая фигура здесь лишняя. не относится к многоугольникам? (Угол)

— Какие бывают углы? (Остроугольные, тупоугольные, прямоугольные)

— У кого сошлась самооценка?

— Кто ошибся в оценке себя?

— В чем допустили ошибки?

ВЫВОД: Будьте внимательны, мы учимся самоконтролю.

8. Графический диктант

Новые понятия появляются на экране.

— Сейчас мы выполним графический диктант и узнаем с каким геометрическим телом мы познакомимся на уроке.

— Поставьте точку, обозначьте ее латинской буквой А, затем отсчитайте 5 клеточек вправо, обозначьте буквой B, от В пять клеточек вверх, обозначьте буквой С, от этой точки 5 клеточек влево, обозначьте буквой Д; от А 3 клеточки по диагонали вправо вверх обозначьте Е; от В по диагонали вправо вверх 3 клеточки, обозначьте F, от Д вправо вверх 3 клеточки по диагонали обозначьте К, от С вправо вверх по диагонали 3 клеточки, обозначьте М.

9. Знакомство с кубом.

— Как называется это геометрическое тело? (КУБ)

*Это слово иностранное, иначе его называют шестигранник.

— Где вы встречали куб? (игра «Кубик Рубика», кубики для игры, кубики конструктора.)

Вот каркас куба из проволоки

(Помощники раздают кубики)

— Возьмите куб. положите его на левую руку.

Какой фигурой является грань куба? (Квадрат)

Поверхность каждого куба состоит из квадратов, которые называются ГРАНЬ.

— Почему он называется правильным шестиугольником?

— Сосчитайте грани куба. Сколько их? (6)

— Две соседние грани квадрата (многогранника) называются РЕБРОМ.

— Покажите ручкой (указкой) ребро

— Сосчитайте сколько у куба ребер? (12)

— Равны ли ребра по длине? (да)

— Сколько ребер пересекается (сходится) к одной вершине? (3)

— Сосчитайте сколько вершин у куба? (8)

Работа в тетради на печатной основе (стр. 8, зад. 12,13)

Изготовление развертки куба по технологической инструкции.

Появляется на экране:

— Сейчас мы сами изготовим развертку куба. Что такое развертка?

*Это как бы разрезанный куб на бумаге. (Показать)

НАПОМНИТЬ об осторожном обращении с ножницами, клеем, экономии бумаги.

— Покажите на кубе его вершины, ребра, грани.

Конструирование из кубов группами

Давайте вспомним правила работы в группах (внимательно слушай товарища, говори по очереди, не перебивай друга, помоги товарищу.

— Как вы думаете от кого зависит успех нашего урока? (От работы каждого из нас)

Варианты работ учащихся

10. Итог урока (на электрифицированном стенде)

— Сколько у куба вершин? (8)

— Сколько к куба ребёр? (12)

— Как называется правильный шестигранник? (куб)

— Что является гранью куба? (квадрат)

б) Рефлексивно-оценочная деятельность

Оцените свою работу на уроке. (Лесенка успеха)

11. Домашнее задание.

Выполнить задание по карточкам по выбору,

Раскрасить ту фигуру, которая является разверткой куба.

Источник