какова вероятность что на обеих костях выпадет число 6
Решение задач о бросании игральных костей
Обычно задача звучит так: бросается одна или несколько игральных костей (обычно 2, реже 3). Необходимо найти вероятность того, что число очков равно 4, или сумма очков равна 10, или произведение числа очков делится на 2, или числа очков отличаются на 3 и так далее.
Ознакомившись с методами решения, вы сможете скачать супер-полезный Excel-файл для расчета вероятности при бросании 2 игральных костей (с таблицами и примерами).
Одна игральная кость
Пример 1. Игральная кость брошена один раз. Какова вероятность, что выпало четное число очков?
Пример 2. Брошен игральный кубик. Найти вероятность выпадения не менее 5 очков.
Даже не вижу смысла приводить еще примеры, переходим к двум игральным костям, где все интереснее и сложнее.
Две игральные кости
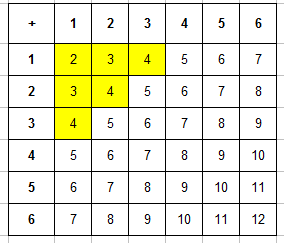
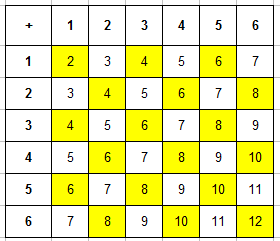
Пример 3. Одновременно бросают 2 игральные кости. Найти вероятность того, что в сумме выпадет менее 5 очков.
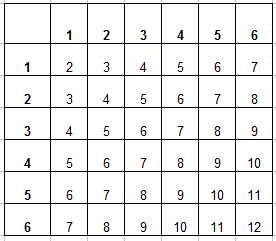
Вот и пришло время заполнять таблицу. В каждую ячейку занесем сумму числа очков выпавших на первой и второй кости и получим уже вот такую картину:
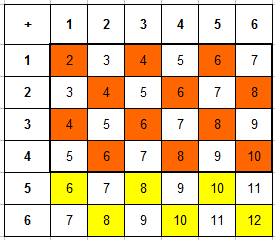
Пример 4. Брошены две игральные кости. Найти вероятность того, что произведение числа очков делится на 3.
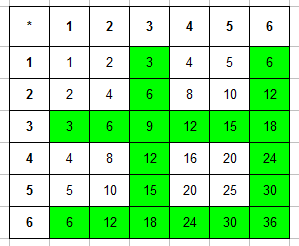
Составляем таблицу произведений очков, выпавших на первой и второй кости. Сразу выделяем в ней те числа, которые кратны 3:
Как видно, и этот тип задач при должной подготовке (разобрать еще пару тройку задач) решается быстро и просто. Сделаем для разнообразия еще одну задачу с другой таблицей (все таблицы можно будет скачать внизу страницы).
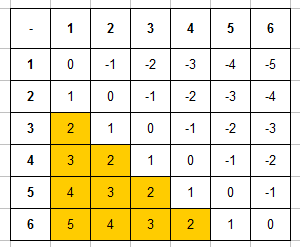
Пример 5. Игральную кость бросают дважды. Найти вероятность того, что разность числа очков на первой и второй кости будет от 2 до 5.
Запишем таблицу разностей очков, выделим в ней ячейки, в которых значение разности будет между 2 и 5:
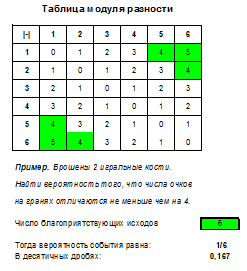
Итак, в случае, когда речь идет о бросании 2 костей и простом событии, нужно построить таблицу, выделить в ней нужные ячейки и поделить их число на 36, это и будет вероятностью. Помимо задач на сумму, произведение и разность числа очков, также встречаются задачи на модуль разности, наименьшее и наибольшее выпавшее число очков (подходящие таблицы вы найдете в файле Excel).
Другие задачи про кости и кубики
Конечно, разобранными выше двумя классами задач про бросание костей дело не ограничивается (просто это наиболее часто встречаемые в задачниках и методичках), существуют и другие. Для разнообразия и понимания примерного способа решения разберем еще три типовых примера: на бросание 3 игральных костей, на условную вероятность и на формулу Бернулли.
Пример 6. Бросают 3 игральные кости. Найдите вероятность того, что в сумме выпало 15 очков.
В случае с 3 игральными костями таблицы составляют уже реже, так как их нужно будет аж 6 штук (а не одна, как выше), обходятся простым перебором нужных комбинаций.
Теперь подберем такие исходы, которые дают в сумме 15 очков.
Пример 7. Бросают 2 игральные кости. Найти вероятность того, что на первой кости выпало не более 4 очков, при условии, что сумма очков четная.
Пример 8. Игральный кубик брошен 4 раза. Найти вероятность того, что четное число очков выпадет ровно 3 раза.
В случае, когда игральный кубик бросается несколько раз, а речь в событии идет не о сумме, произведении и т.п. интегральных характеристиках, а лишь о количестве выпадений определенного типа, можно для вычисления вероятности использовать формулу Бернулли.
Приведем еще пример, решаемый аналогичным образом.
Пример 9. Игральную кость бросают 8 раз. Найти вероятность того, что шестёрка появится хотя бы один раз.
Полезные ссылки
Для наглядного и удобного расчета вероятностей в случае бросания двух игральных костей я сделала
Файл с таблицами для расчета вероятности.
В нем приведены таблицы суммы, произведения, разности, минимума, максимума, модуля разности числа очков.
Вводя число благоприятствующих исходов в специальную ячейку вы получите рассчитанную вероятность (в обычных и десятичных дробях). Файл открывается программой Excel.
Еще по теории вероятностей:
В решебнике вы найдете более 400 задач о бросании игральных костей и кубиков с полными решениями (вводите часть текста для поиска своей задачи):
Вероятность игральной кости.
Задачи на вероятность игральной кости не менее популярны, чем задачи о подбрасывании монет. Условие такой задачи обычно звучит так: при бросании одной или нескольких игральных костей (2 или 3), какова вероятность того, что сумма очков будет равна 10, или число очков равно 4, или произведение числа очков, или делится на 2 произведение числа очков и так далее.
Применение формулы классической вероятности является основным методом решения задач такого типа.
Одна игральная кость, вероятность.
Задача 1. Один раз брошена игральная кость. Какова вероятность выпадения четного числа очков?
Поскольку игральная кость собой представляет кубик (или его еще называют правильной игральной костью, на все грани кубик выпадет с одинаковой вероятностью, так как он сбалансированный), у кубика 6 граней (число очков от 1 до 6, которые обычно обозначаются точками), это значит, что в задаче общее число исходов: n=6. Событию благоприятствуют только исходы, при которых выпадает грань с четными очками 2,4 и 6, у кубика таких граней: m=3. Теперь можем определить искомую вероятность игральной кости: P=3/6=1/2=0.5.
Задача 2. Брошен один раз игральный кубик. Какова вероятность, что выпадет не менее 5 очков?
Решается такая задача по аналогии с примером, указанным выше. При бросании игрального кубика общее число равновозможных исходов равно: n=6, а удовлетворяют условие задачи (выпало не менее 5 очков, то есть выпало 5 или 6 очков) только 2 исхода, значит m=2. Далее находим нужную вероятность: P=2/6=1/3=0.333.
Две игральные кости, вероятность.
Задача 3. Брошены одновременно 2 игральные кости. Какова вероятность выпадения суммы менее 5 очков?
Теперь можно заполнить таблицу, для этого в каждую ячейку заносится число суммы очков, которые выпали на первой и второй кости. Заполненная таблица выглядит так:
Благодаря таблице определим число исходов, которые благоприятствуют событию » выпадет в сумме менее 5 очков». Произведем подсчет числа ячеек, значение суммы в которых будет меньше числа 5 (это 2, 3 и 4). Такие ячейки для удобства закрашиваем, их будет m=6:
Учитывая данные таблицы, вероятность игральной кости равняется: P=6/36=1/6.
Задача 4. Было брошено две игральные кости. Определить вероятность того, что произведение числа очков будет делиться на 3.
Для решения задачи составим таблицу произведений очков, которые выпали на первой и на второй кости. В ней сразу же выделим числа кратные 3:
Записываем общее число исходов эксперимента n=36 (рассуждения такие же как в предыдущей задаче) и число благоприятствующих исходов (число ячеек, которые закрашены в таблице) m=20. Вероятность события равняется: P=20/36=5/9.
Задача 5. Дважды брошена игральная кость. Какова вероятность, что на первой и второй кости разность числа очков будет равна от 2 до 5?
Чтобы определить вероятность игральной кости запишем таблицу разностей очков и выделим в ней те ячейки, значение разности в которых будет между 2 и 5:
Число благоприятствующих исходов (число ячеек, закрашенных в таблице) равно m=10, общее число равновозможных элементарных исходов будет n=36. Определит вероятность события: P=10/36=5/18.
В случае простого события и при бросании 2-х костей, требуется построить таблицу, затем в ней выделить нужные ячейки и их число поделить на 36, это и будет считаться вероятностью.
какова вероятность того, что при бросании двух игральных костей, хотя бы один раз выпадет 6 очков
У каждой кости есть 6 граней, есть 2 кости, значит есть 6^2 (шесть во второй степени) = 36 вариантов «расклада» (выпадания костей) :
Из этих 36 вариантов есть 11 «удачных» ситуаций (когда хотя бы на одной кости выпала шестёрка) :
1-6
2-6
3-6
4-6
5-6
6-6
6-5
6-4
6-3
6-2
6-1
итого получается вероятность 11/36
предыдущий ответ неправильный так как комбинация 6 6 встречается дважды
строго по теории вероятность выпадения шестерки на одном кубике 1/6
при двух кубиках вероятности складываются
Обычная формула перемножения вероятностей, но в этом случае надо посчитать «вероятность проигрыша» а потом вычесть из 100%.
Отрицание
Вот ещё одна полезная подсказка: иногда сложно посчитать вероятность того, что событие наступит, зато легче определить шансы, что событие не наступит. Например, предположим, у нас есть ещё одна игра: вы бросаете 6d6 и выигрываете, если хотя бы один раз выпадет 6. Какова вероятность выигрыша?
В данном случае нужно учесть много вариантов. Возможно, выпадет одно число 6, то есть на одной из игральных костей выпадет число 6, а на других — числа от 1 до 5, тогда есть 6 вариантов того, на какой из игральных костей будет 6. Вам может выпасть число 6 на двух игральных костях, или на трёх, или на ещё большем количестве, и каждый раз нужно будет делать отдельный подсчёт, поэтому здесь легко запутаться.
Но давайте посмотрим на задачу с другой стороны. Вы проиграете, если ни на одной из игральных костей не выпадет число 6. В данном случае у нас есть 6 независимых испытаний. Вероятность того, что на каждой из игральных костей выпадет число, не равное 6, составляет 5/6. Перемножьте их — и получите примерно 33%. Таким образом, вероятность проигрыша составляет один к трём. Следовательно, вероятность выигрыша — 67% (или два к трём).
Из этого примера очевидно: если вы считаете вероятность того, что событие не наступит, нужно вычесть результат из 100%. Если вероятность выиграть равна 67%, то вероятность проиграть — 100% минус 67%, или 33%, и наоборот. Если сложно посчитать одну вероятность, но легко посчитать противоположную, посчитайте противоположную, а затем вычтите это число из 100%.
Какова вероятность что из 4-х брошенных костей хотя бы на одной выпадет 6?
Ответы:
У задачи забавная история. В оригинале она звучала несколько иначе.
Известный французский игрок XVII века шевалье Де Мере (это литературный псевдоним, его настоящее имя Антуан Гомбо) обнаружил, что
Расчеты по законам теории вероятностей это подтверждают. Действительно, при 4-х бросаниях «правильной» кости, число равновозможных исходов равно 6⁴ = 1296. Но, среди них будет 5⁴ = 625 таких, где 6 не появилось ни разу! Стало быть, в остальных 1296 − 625 = 671 случаях 6 выпадет хотя бы один раз. Значит, искомая вероятность равна
Р = 671 / 1296 ≈ 0,52 > 1/2.
Партнеры Де Мере по игре быстро «увидели» его секрет, и он решил придумать новый вариант игры. Де Мере рассудил так: при бросании пары костей, выпадение дубля 6х6, событие в 6 раз менее вероятное, чем выпадение шестёрки при бросании одной кости. Он, конечно, в этом был прав! И Де Мере решил:
Де Мере не был математиком. Более того, он не доверял математике. Он искренне был уверен в своих вычислениях. Но, проведенный эксперимент с костями, не подтвердил его выводы. Этот эмпирический метод применяют до сих пор, он называется «метод Монте-Карло».
Де Мере пришел в ярость и написал гневное письмо Блезу Паскалю. Это письмо вошло в историю! Его цитируют до сих пор в книгах по теории вероятностей. Утверждают, что Де Мере выражал в письме сожаление, что не может вызвать Паскаля на дуэль, поскольку тот не дворянского происхождения.
Паскаль, конечно, объяснил причину. Рассуждая аналогично первому случаю, здесь искомая вероятность равна
Р = (36²⁴ − 35²⁴)/36²⁴ = 1 − (35/36)²⁴ ≈ 0,48 30864
Это по вероятности при условии что выпадет только одна кость с 6
Подставляем в формулу Бернулли следующие значения: n=1 (число бросков), p=1/6 (вероятность появления 6 при одном броске), k≥1 (хотя бы один раз появится шестерка). Прежде чем вычислять эту вероятность, напомню, что практически все задачи с формулировкой «хотя бы один. » удобно решать, переходя к противоположному событию «ни одного. «.
Тогда искомая вероятность будет равна
P1(k≥1)=1−P1(0)=1−(5 /6)=0,833333333333333 3
В комбинаторике вычисляют не так, а берут перемножают последние числа и делят на первые. Точно так же как в спорт лото 6 из 36-ти. Мне приходилось создавать программу и поэтому я повторяла пройденный в школе материал.
100% / 15 = 6,66666666667%
Округляем, вероятность выпадания хоть одной шестёрки 6,7%
2-х делим на 2, 4-х на 4 получаем 1,67%
Но вероятность рассчитывается для одной в основном.
А теперь попробуйте самостоятельно высчитать вероятность выигрыша в спорт лото 6 из 36-ти.
Всего у кубика 6 граней. Всего возможных комбинаций при выкидывании 4 костей 6*6*6*6=1296. Вероятность что при бросании кубика выпадет «шестёрка» = 1/6. Или 216/1296. Но нас устроит и вариант выпадания двух шестёрок и трёх и даже четырёх шестёрок. Тогда вероятность выпадения двух шестёрок 36/1296, выпадение трёх шестёрок 6/1296, всех четврёх шестёрок 1/1296. Все эти вероятности надо сложить.
216/1296+36/1296+6/1 296+1/1296 =259/1296. Это вероятность что в результате броска 4 кубиков выпадет хотя бы одна шестёрка. Это примерно 0.1998. Около 20%.
Количество исходов для одной кости N1=6 (х-1,2,3,4,5,6)
Количество исходов для четырех костей N2=6^4=1296
Давайте посчитаем вероятность того, что не на одной из костей не выпадет 6, а потом вычтем из единицы полученный результат, и получим интересующий нас ответ.
И того правильный ответ:
ПОМОГИТЕ с задачами по теории вероятности
— число тех исходов, которые благоприятствуют событию.
Пример 1. Игральная кость брошена один раз. Какова вероятность, что выпало четное число очков?
Так как игральная кость представляет собой кубик (еще говорят, правильная игральная кость, то есть кубик сбалансированный, так что выпадает на все грани с одинаковой вероятностью), граней у кубика 6 (с числом очков от 1 до 6, обычно обозначаемых точкам), то и общее число исходов в задаче n=6
. Благоприятствуют событию только такие исходы, когда выпадет грань с 2, 4 или 6 очками (только четные), таких граней m=3. Тогда искомая вероятность равна P=3/6=1/2=0.5
Пример 2. Брошен игральный кубик. Найти вероятность выпадения не менее 5 очков.
Рассуждаем также, как и в предыдущем примере. Общее число равновозможных исходов при бросании игрального кубика n=6
, а условию «выпало не менее 5 очков», то есть «выпало или 5, или 6 очков» удовлетворяют 2 исхода, m=2. Нужная вероятность равна P=2/6=1/3=0.333
Даже не вижу смысла приводить еще примеры, переходим к двум игральным костям, где все интереснее и сложнее.
Две игральные кости
Пример 3. Одновременно бросают 2 игральные кости. Найти вероятность того, что в сумме выпадет менее 5 очков.
(и им соответствуют как раз 36 ячеек в таблице исходов).
Вот и пришло время заполнять таблицу. В каждую ячейку занесем сумму числа очков выпавших на первой и второй кости и получим уже вот такую картину:
таблица суммы очков при бросании 2 игральных костей
Теперь эта таблица поможем нам найти число благоприятствующих событию «в сумме выпадет менее 5 очков» исходов. Для этого подсчитаем число ячеек, в которых значение суммы будет меньше 5 (то есть 2, 3 или 4). Для наглядности закрасим эти ячейки, их будет m=6
:
таблица суммы очков менее 5 при бросании 2 игральных костей
Тогда вероятность равна: P=6/36=1/6
Пример 4. Брошены две игральные кости. Найти вероятность того, что произведение числа очков делится на 3.
Составляем таблицу произведений очков, выпавших на первой и второй кости. Сразу выделяем в ней те числа, которые кратны 3:
таблица произведения очков при бросании 2 игральных костей
Остается только записать, что общее число исходов n=36
(см. предыдущий пример, рассуждения такие же), а число благоприятствующих исходов (число закрашенных ячеек в таблице выше) m=20. Тогда вероятность события будет равной P=20/36=5/9
Как видно, и этот тип задач при должной подготовке (разобрать еще пару тройку задач) решается быстро и просто. Сделаем для разнообразия еще одну задачу с другой таблицей (все таблицы можно будет скачать внизу страницы).
Пример 5. Игральную кость бросают дважды. Найти вероятность того,