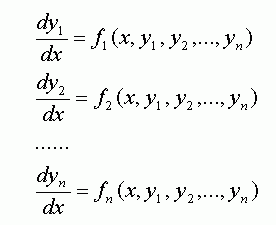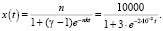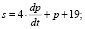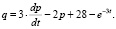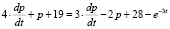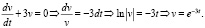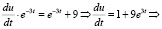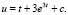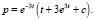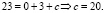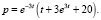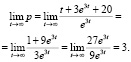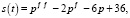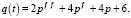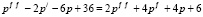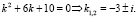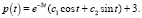В математической модели часто используют дифференциальные уравнения потому что

В математической модели часто используют дифференциальные уравнения потому что

Математика\ 1.Дифференциальные и интегральные уравне­ния

Воловик Е.А. , Силенко В.Е.

Донецкий национальный университет экономики и торговли

имени Михаила Туган-Барановского, Украина

Роль дифференциальных уравнений в построении математической модели реального мира

Понятия, созданные современной математикой, зачастую кажутся весьма далекими от реального мира. Но именно с их помощью людям удалось проникнуть в тайны строения атомного ядра, рассчитать движение космических кораблей, создать весь тот мир техники, на котором основано современное производство. Одним из основных методов познания природы является опыт, эксперимент. С помощью экспериментов были установлены многие законы природы (закон сохранения вещества и энергии, периодическая система элементов Д.И. Менделеева и т.д.). Однако не всегда целесообразно проводить эксперимент. За последнее столетие в самых различных областях науки и техники все большую роль стал играть метод математического моделирования.

Чтобы изучить какое-нибудь явление природы или работу машины, предварительно изучают всевозможные связи между величинами, их характеризующими. Затем полученные связи выражают математически и приходят к системе уравнений. Решая эти уравнения или системы уравнений, ученые и инженеры делают выводы о том, как в дальнейшем будет развиваться это явление или как будет работать машина, что надо сделать, чтобы получить требуемые результаты.

При этом уравнения и системы уравнений бывают алгебраическими и дифференциальными. Чтобы получить уравнения, допускающие решения, приходиться упрощать задачу, отбрасывая некоторые величины как несущественные. Но чем точнее нужен результат, тем больше величин приходиться учитывать, тем сложнее получается математическая модель.

Математические модели, которые строили в 19 веке, были сравнительно простыми. Но возрастающие требования к точности ответа, развитие техники, познание разнообразных явлений привели к построению все более сложных математических моделей.

Сейчас с помощью математического моделирования решают такие задачи, как описание природы морей и океанов, распада радиоактивных веществ, перевод текстов с одного языка на другой и т.п. Появилась возможность строить математические модели экономики, применять математику в изучении общественных явлений.

Теория дифференциальных уравнений является одним из самых больших разделов современной математики. Чтобы охарактеризовать её место в современной математической науке, прежде всего, необходимо подчеркнуть основные особенности теории дифференциальных уравнений.

Первая особенность – это непосредственная связь теории дифференциальных уравнений с приложениями. Характеризуя математику как метод проникновения в тайны природы, можно сказать, что основным путем применения этого метода является формирование и изучение математических моделей реального мира. Изучая какие-либо физические явления, исследователь, прежде всего, создает его математическую идеализацию или, другими словами, математическую модель, то есть, пренебрегая второстепенными характеристиками явления, он записывает основные законы, управляющие этим явлением, в математической форме. Очень часто эти законы можно выразить в виде дифференциальных уравнений. Такими оказываются модели различных явлений механики сплошной среды, химических реакций, электрических и магнитных явлений и др.

Исследуя полученные дифференциальные уравнения вместе с дополнительными условиями, которые, как правило, задаются в виде начальных и граничных условий, математик получает сведения о происходящем явлении, иногда может узнать его прошлое и будущее. Изучение математической модели математическими методами позволяет не только получить качественные характеристики физических явлений и рассчитать с заданной степенью точности ход реального процесса, но и дает возможность проникнуть в суть физических явлений, а иногда предсказать и новые физические эффекты. Бывает, что сама природа физического явления подсказывает и подходы, и методы математического исследования. Критерием правильности выбора математической модели является практика, сопоставление данных математического исследования с экспериментальными данными.

Для составления математической модели в виде дифференциальных уравнений нужно, как правило, знать только локальные связи и не нужна информация обо всем физическом явлении в целом. Математическая модель дает возможность изучать явление в целом, предсказать его развитие, делать качественные оценки измерений, происходящих в нем с течением времени. На основе анализа дифференциальных уравнений были открыты электромагнитные волны, и только после экспериментального подтверждения Герцем фактического существования электромагнитных колебаний стало возможным рассматривать уравнения Максвелла как математическую модель реального физического явления.

Итак, первая черта теории дифференциальных уравнений – ее тесная связь с приложениями. Другими словами, можно сказать, что теория дифференциальных уравнений родилась из приложений. В этом своем разделе – теории дифференциальных уравнений – математика, прежде всего, выступает как неотъемлемая часть естествознания, на которой основывается вывод и понимание количественных и качественных закономерностей, составляющих содержание наук о природе. Именно естествознание является для теории дифференциальных уравнений источником новых проблем, оно в значительной мере определяет направление их исследований, дает правильную ориентацию этим исследованиям. Более того, дифференциальные уравнения не могут плодотворно развиваться в отрыве от физических задач.

Второй особенностью теории дифференциальных уравнений является ее связь с другими разделами математики, такими, как функциональный анализ, алгебра и теория вероятностей. Теория дифференциальных уравнений и особенно теория уравнений с частными производными широко используют основные понятия, идеи и методы этих областей математики и, более того, влияют на их проблематику и характер исследований. Некоторые большие и важные разделы математики были вызваны к жизни задачами теории дифференциальных уравнений. В теории дифференциальных уравнений ясно прослеживается основная линия развития математики: от конкретного и частного через абстракцию к конкретному и частному.

Многие разделы теории дифференциальных уравнений так разрослись, что стали самостоятельными науками. Можно сказать, что большая часть путей, связывающих абстрактные математические теории и естественнонаучные приложения, проходит через дифференциальные уравнения. Все это обеспечивает теории дифференциальных уравнений почетное место в современной науке.

Источник

Где применяются дифференциальные уравнения

Содержание статьи

В биологии:

Первой содержательной математической моделью, описывающей биологические сообщества была модель Лотки — Вольтерры. Она описывает популяцию, состоящую из двух взаимодействующих видов. Первый из них, именуемый хищниками, при отсутствии второго вымирает по закону x′ = –ax (a > 0), а второй — жертвы — при отсутствии хищников неограниченно размножается в соответствии с законом Мальтуса. Взаимодействие двух этих видов моделируется так. Жертвы вымирают со скоростью, равной числу встреч хищников и жертв, которое в данной модели предполагается пропорциональным численности обеих популяций, т. е. равной dxy (d > 0). Поэтому y′ = by – dxy. Хищники же размножаются со скоростью, пропорциональной числу съеденных жертв: x′ = –ax + cxy (c > 0). Система уравнений
x′ = –ax + cxy, (1)
y′ = by – dxy, (2)
описывающая такую популяцию хищник — жертва и называется системой (или моделью) Лотки — Вольтерры.

В физике:

Второй закон Ньютона можно записать в форме дифференциального уравнения
m((d^2)x)/(dt^2) = F(x,t),
где m — масса тела, x — его координата, F(x, t) — сила, действующая на тело с координатой x в момент времени t. Его решением является траектория движения тела под действием указанной силы.

В экономике:

Модель естественного роста выпуска
Будем полагать, что некоторая продукция продается по фиксированной цене Р. Обозначим через Q(t) количество продукции, реализованной на момент времени t; тогда на этот момент времени получен доход, равный PQ(t). Пусть часть указанного дохода расходуется на инвестиции в производство реализуемой продукции, т.е.
I(t)=mPQ(t), (1)

где m — норма инвестиции — постоянное число, причем 0

Источник

В математической модели часто используют дифференциальные уравнения потому что

Для создания экономически развитого общества, активного продвижения научно-технического прогресса особая роль отводится высшей математике. Современные ученые используют для исследования экономических процессов методы математического анализа, регрессионного анализа, теории игр, линейного программирования, матричного и векторного исчислений и т.п., которые в свою очередь являются составляющими математического моделирования. Одним из важнейших разделов математики, который имеет большое прикладное значение, является раздел «Обыкновенные дифференциальные уравнения». Кроме общематематического и теоретического интереса, дифференциальные уравнения находят широкое практическое применение. Например, при решении задач, связанных с оптимальным управлением, экономической деятельностью фирмы или предприятия, организацией производственного процесса и т.д. В виде дифференциальных уравнений записываются соотношения между экономическими переменными, такими как цены, заработная плата, капитал, процентная ставка и др.

Основу экономической теории составляют экономические законы, выраженные в виде количественных соотношений между величинами, характеризующими экономическую систему, или процесс. Такие законы дают возможность исследовать реальные экономические системы на основе математических моделей. Построение и изучение этих моделей составляет предмет математической экономики, которая рассматривает экономику как сложную динамическую систему.

В исследовании метод моделирования является важнейшим универсальным методом. Модель – «это объект или явление, аналогичные, т.е. в достаточной степени повторяющие свойства моделируемого объекта или явления (прототипа), существенные для целей конкретного моделирования, и опускающие несущественные свойства, в которых они могут отличаться от прототипа» [1]. Модель какой-либо сложной системы тоже представляет собой систему (и нередко весьма сложную), имеющую физическое воплощение либо записанную с помощью слов, цифр, математических обозначений, графических изображений и т. д. Таким образом, можно сказать, что модель – это физическая или знаковая система, имеющая объективное подобие с исследуемой системой в отношении функциональных, а часто и структурных характеристик, являющихся предметом исследования.

Математическая модель представляет собой совокупность уравнений, неравенств, функционалов, логических условий и других соотношений, отражающих взаимосвязи и зависимости основных характеристик моделируемой системы. Однако важное преимущество модели состоит в том, что необъятная с точки зрения полного описания реальная социально-экономическая система заменяется пусть даже непростой, но вполне доступной для анализа и расчетов моделью, которая вместе с тем сохраняет в себе все существенное, что интересует исследователя. Это существенное выступает в модели даже более четко и рельефно, не будучи затемнено всевозможными незначащими частностями и деталями, посторонними и случайными факторами. Модель, возникшая в результате построения, позволяет исследователю экспериментировать с различными параметрами, переменными величинами, условиями и ограничениями и выяснять, к каким возможным результатам это приводит [2].

Для изучения математических моделей экономики, помимо экономической науки, необходимо владеть математическими методами, среди которых аппарат дифференциальных уравнений играет важную роль. Экономические закономерности, как правило, представляют собой сложные нелинейные соотношения между экономическими величинами, явный вид которых непосредственно установить затруднительно. При наличии устойчивой закономерности малые изменения величин можно приближенно заменить дифференциалами. Тогда нелинейные соотношения между величинами, соответственно, заменяются более простыми линейными соотношениями между величинами и их производными. Эти соотношения представляют собой дифференциальные уравнения, с помощью которых строится математическая модель экономической системы или процесса.

Примеры моделей экономических процессов, основу которых составляют дифференциальные уравнения, приведем по сложности используемых уравнений (от простых к сложным). Рассмотрим модели процессов, в которых возникает необходимость использования теории дифференциальных уравнений с разделяющимися и разделёнными переменными. К задачам такого типа относятся, например, задачи об эффективности рекламы, изменении численности населения, зависимость спроса или предложения от цены товара, зависимость функции спроса от эластичности, истощение ресурсов Земли или рост населения, рост денежного вклада в банке и другие.

Пример 1. (Эффективность рекламы). Фирма подготовила для реализации новый продукт. Для его продвижения была проведена рекламная компания, в результате которой о новинке из 10000 потенциальных покупателей узнали 2500 человек. После этого сведения о новом товаре распространяются с помощью передачи информации от одного человека к другому. Обозначим через x(t) число покупателей, знающих о новинке в момент времени t. Изменение этой величины будет пропорционально как числу покупателей, знающих о новинке, так и не знающих о ней, а также промежутку времени dt, за который это изменение происходит, то есть dx = kx(n – x)dt, где п – общее число потенциальных покупателей новинки (в нашем случае п = 10000), k – коэффициент пропорциональности (будем считать, что k = 2?10-6 чел./день), n – x – число покупателей, не знающих о новинке (n – x = 10000 – 2500 = 7500) Используя уравнение логистической кривой [3], получим зависимость x(t) с учетом данных нашей задачи:

Предположим, что t = 20 дней, тогда x(20) = 3321, т.е. за 20 дней о новинке будут знать приблизительно 3321 покупатель.

Допустим теперь, что t = 30, тогда о новинке будут знать приблизительно x(20) = 3778 покупателей. Таким образом, за 30 дней о новинке будут знать 6278 человек.

Пример 2. (Спрос и предложение). Спрос и предложение – экономические категории товарного производства, возникающие и функционирующие на рынке, в сфере товарного обмена. Рассмотрим какой-нибудь товар. Обозначим через p цену на товар, а через 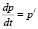– так называемую тенденцию формирования цены (производную цены во времени). Рассмотрим случай, когда спрос и предложение зависят от скорости изменения цены [3, с. 10]. В зависимости от разных факторов спрос и предложение могут быть различными функциями цены и тенденции формирования цены. Одним из экономических законов товарного производства является закон спроса и предложения, который заключается во взаимозависимости спроса и предложения и их объективном стремлении к соответствию. Для экономики представляет интерес условие, при котором спрос равен предложению, т.е. s(p, p/) = q(p, p/). При этом цена p = p0 называется равновесной. Обе функции s и q являются линейными относительно переменных р и р/. Следовательно, решение задач на спрос и предложение приводит к необходимости использования теории линейных дифференциальных уравнений первого порядка. Описание методов решения таких уравнений можно найти в [4].

Например, функции спроса и предложения имеют вид:

Равновесие между спросом и предложением сохраняются при условии при условии

или, когда выполняется равенство

(1)

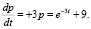
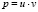
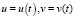
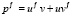
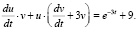
В результате получено линейное неоднородное дифференциальное уравнение первого порядка с постоянными коэффициентами. Для его решения применим метод И. Бернулли: общее решение ищем в виде , где . Тогда . Подставляя р и р/ в (1), приходим к уравнению

(2)

Подставляя найденное значение v в уравнение (2), найдем и:

Общее решение уравнения (1) запишется в виде

Найдем зависимость равновесной цены от времени, если в начальный момент p = 23:

Таким образом, искомая зависимость имеет вид

Чтобы узнать является ли данная равновесная цена устойчивой, найдем limt→∞ p при этом получающуюся в ходе вычислений неопределённость 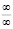будем раскрывать по правилу Лопиталя.

Следовательно, равновесная цена является устойчивой.

Пример 3. (Модель рынка с прогнозируемыми ценами). В данной модели используется теория линейных дифференциальных уравнений второго порядка. Обычно в простых моделях рыночной экономики спрос и предложение зависят от текущей цены на товар. Однако в реальных ситуациях существует зависимость от тенденции ценообразования и темпов изменения цены. В моделях с непрерывными и дифференцируемыми по времени t функциями эти характеристики описываются соответственно первой и второй производными функции цены p(t). Например, пусть функции спроса s(t) и предложения q(t) имеют следующие зависимости от цены р:

Принятые зависимости реалистичны, так как если темп цены растет (р// > 0), то интерес к товару на рынке то же растет и наоборот, если темп цены падает, то и интерес к товару падает. Причем быстрый рост цены отпугивает покупателя, поэтому слагаемое с первой производной функции цены входит со знаком минус. В то же время темп изменения цены влияет на усиление предложения (рост цены увеличивает предложение), поэтому слагаемое, содержащее р/, входит в q(t) со знаком плюс. Установим зависимость цены от времени. Воспользуемся, как и в предыдущем примере, условием равновесного состояния рынка s(t) = q(t). Исходя из этого условия, получаем уравнение

(3)

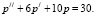
Получено линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его общее решение складывается из общего решения соответствующего однородного уравнения и частного решения данного неоднородного уравнения [5, с.73-81].

Общее решение однородного уравнения найдем исходя из вида корней характеристического уравнения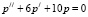

Так как корни характеристического уравнения являются комплексными, то общее решение однородного уравнения имеет вид 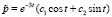, где c1 и c2 – произвольные постоянные.

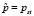
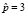
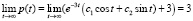
В качестве частного решения возьмем постоянную установившуюся цену . Подставляя это значение в формулу (3), найдем, что . Таким образом общее решение уравнения (3) имеет вид:

,

делаем заключение: все интегральные кривые имеют горизонтальную асимптоту p = 3. Это означает, что все цены стремятся к устоявшейся цене 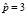с колебаниями около неё, причем амплитуда колебаний затухает со временем.

Из рассмотренных задач можно сделать вывод, что методы моделирования с помощью дифференциальных уравнений широко применяются для решения экономических задач. Анализ полученных общих и частных решений позволяет выявить резервы повышения эффективности производства, установить зависимости между спросом и предложением.

Источник

Дифференциальные уравнения как математические модели реальных процессов

Понятие и типы математических моделей, критерии их классификации. Примеры использования дифференциальных уравнений при моделировании реальных процессов: рекламная компания, истечение жидкости, водяные часы, невесомость, прогиб балок, кривая погони.

Дифференциальные уравнения как математические модели реальных процессов

Понятия, созданные современной математикой, часто кажутся весьма далекими от реального мира. Но именно с их помощью людям удалось проникнуть в тайны строения атомного ядра, рассчитать движение космических кораблей, создать весь тот мир техники, на котором основано современное производство. Одним из основных методов познания природы является опыт, эксперимент. С помощью экспериментов были установлены многие законы природы (закон сохранения вещества и энергии, периодическая система элементов Д.И. Менделеева и т.д.). Однако не всегда целесообразно проводить эксперимент. За последнее столетие в самых различных областях науки и техники все большую роль стал играть метод математического моделирования.

Чтобы изучить какое-нибудь явление природы или работу машины, предварительно изучают всевозможные связи между величинами, их характеризующими. Затем полученные связи выражают математически и приходят к системе уравнений. Решая эти уравнения или системы уравнений, ученые и инженеры делают выводы о том, как в дальнейшем будет развиваться это явление или как будет работать машина, что надо сделать, чтобы получить требуемые результаты.

При этом уравнения и системы уравнений бывают алгебраическими и дифференциальными. Чтобы получить уравнения, допускающие решения, приходиться упрощать задачу, отбрасывая некоторые величины как несущественные. Но чем точнее нужен результат, тем больше величин приходиться учитывать, тем сложнее получается математическая модель.

Математические модели, которые строили в XIX веке, были сравнительно простыми. Но возрастающие требования к точности ответа, развитие техники, познание разнообразных явлений привели к построению все более сложных математических моделей.

Все эти модели построены помощью теории дифференциальных уравнений. Это говорит о том, что дифференциальные уравнения выступают как мощное средство моделирования. Развитие теории дифференциальных уравнений позволяло и позволяет двигаться научному прогрессу вперед, а использование в процессе моделирования ЭВМ делает модели еще более сложными, полными и гибкими.

1. Теоретические основы математического моделирования

1.1 Определения математических моделей

математический дифференциальный уравнение

Никакое определение не может в полном объёме охватить реально существующую деятельность по математическому моделированию. Несмотря на это, определения полезны тем, что в них делается попытка выделить наиболее существенные черты.

1) находящаяся в некотором объективном соответствии с познаваемым объектом;

2) способная замещать его в определенных отношениях;

3) дающая при её исследовании, в конечном счете, информацию о самом моделируемом объекте.

1.2 Классификация математических моделей

В основу классификации математических моделей можно положить различные принципы. Можно классифицировать модели по отраслям наук (математические модели в физике, биологии, социологии и т.д.). Можно классифицировать по применяемому математическому аппарату (модели, основанные на применении обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, стохастических методов, дискретных алгебраических преобразований и т.д.). Наконец, если исходить из общих задач моделирования в разных науках безотносительно к математическому аппарату, наиболее естественна такая классификация:

дескриптивные (описательные) модели;

Поясним это на примерах:

Дескриптивные (описательные) модели. Например, моделирование движения кометы, вторгшейся в Солнечную систему, производится с целью предсказания траектории ее полета, расстояния, на котором она пройдет от Земли, и т.д. В этом случае цели моделирования носят описательный характер, поскольку нет никаких возможностей повлиять на движение кометы, что-то в нем изменить.

Оптимизационные модели используются для описания процессов, на которые можно воздействовать, пытаясь добиться достижения заданной цели. В этом случае в модель входит один или несколько параметров, доступных влиянию. Например, меняя тепловой режим в зернохранилище, можно задаться целью, подобрать такой режим, чтобы достичь максимальной сохранности зерна, т.е. оптимизировать процесс хранения.

Многокритериальные модели. Нередко приходится оптимизировать процесс по нескольким параметрам одновременно, причем цели могут быть, весьма противоречивыми. Например, зная цены на продукты и потребность человека в пище, нужно организовать питание больших групп людей (в армии, детском летнем лагере и др.) физиологически правильно и, одновременно с этим, как можно дешевле. Ясно, что эти цели совсем не совпадают, т.е. при моделировании будет использоваться несколько критериев, между которыми нужно искать баланс.

2. Примеры использования дифференциальных уравнений при моделировании реальных процессов

2.1 Модель рекламной компании

Фирма начинает рекламировать новый товар или услугу. Разумеется, что прибыль от будущих продаж должна с лихвой покрывать издержки на дорогостоящую кампанию. Ясно, что вначале расходы могут превышать прибыль, поскольку лишь малая часть потенциальных покупателей будет информирована о новинке. Затем, при увеличении числа продаж, уже возможно рассчитывать на заметную прибыль, и, наконец, наступит момент, когда рынок насытится, и рекламировать товар, далее станет бессмысленно.

В итоге получаем уравнение

В результате этих рассуждений приходим к дифференциальному уравнению

которое можно переписать в виде

Решим теперь следующую задачу. Цилиндрический резервуар с вертикальной осью высотой 6 м и диаметром 4 м имеет на дне круглое отверстие радиусом 1/12 м. Требуется установить зависимость уровня воды в резервуаре от времени t, а также определить время, в течение которого вытечет вся вода.

Интегрируя это дифференциальное уравнение, приходим к соотношению t= 434,304 ; которое и дает искомую зависимость уровня воды от времени t. Если теперь в последнем равенстве положить х=6, то получим, что вся вода вытечет из резервуара приблизительно через 18 минут.

Вторая задача состоит в следующем. Известно, что древние водяные часы представляли собой чашу (рис. 2), из которой через небольшое отверстие на дне вытекала вода. Такие часы использовались в греческих и римских судах для хронометрирования речей адвокатов, чтобы не допускать слишком долгих выступлений. Требуется найти форму водяных часов, при которой уровень воды убывал бы в чаше с постоянной скоростью.

Задача легко решается с помощью выведенного выше уравнения (6), которое мы только перепишем в виде

Именно, учитывая, что чашу можно рассматривать как поверхность вращения, в соответствии с обозначениями на (рис. 2) из уравнения (7) получаем, что

Где a=U_x= — проекция свободной поверхности жидкости на ось x, которая по условию задачи есть величина постоянная. Возведя обе части уравнения (8) в квадрат приходим к уравнению

где c=a 2 р 2 /(2gk 2 s 2 ). Последнее означает, что форма поверхности водяных часов получается вращением кривой (9) вокруг оси х.

Приведем один из примеров использования дифференциальных уравнений для выбора правильной стратегии при решении задач поиска.

Пусть, например, миноносец охотится за подводной лодкой в густом тумане. В какой-то момент времени туман поднимается и подводная лодка оказывается обнаруженной на поверхности воды на расстоянии 3 миль от миноносца. Скорость миноносца вдвое больше скорости подводной лодки. Требуется определить траекторию (кривую погони), по которой должен следовать миноносец, чтобы он прошел точно над подводной лодкой, если последняя сразу же погрузилась после ее обнаружения и ушла на полной скорости прямым курсом в неизвестном направлении.

Для решения сформулированной задачи введем полярные координаты r, O таким образом, чтобы полюс О находился в точке обнаружения подводной лодки, а полярная ось r проходила через точку, в которой в момент обнаружения подводной лодки был миноносец (рис. 3). Дальнейшие рассуждения основаны на следующих соображениях. Прежде всего, миноносцу надо занять такую позицию, чтобы он и подводная лодка находились на одном расстоянии от полюса О. Затем миноносец должен двигаться вокруг полюса О по такой траектории, чтобы оба движущихся объекта все время находились на одинаковом расстоянии от точки О. Только в этом случае миноносец, обходя вокруг полюса О, пройдет над подводной лодкой. Из вышесказанного следует, что сначала миноносец должен идти прямым курсом к точке О до тех пор, пока он не окажется на том же расстоянии х от полюса О, что и подводная лодка.

Очевидно, что расстояние х можно найти либо из уравнения

Теперь, если «встречи» не произошло, то миноносец должен в дальнейшем двигаться вокруг полюса О (по направлению движения часовой стрелки или против), удаляясь от последнего со скоростью подводной лодки u. Разложим скорость миноносца 2u на две составляющие: радиальную u_r и тангенциальную u_t (рис. 3).

Итак решение исходной задачи сводится к решению системы двух дифференциальных уравнений

Которая, в свою очередь, может быть сведена к одному уравнению

исключением переменной t.

Решая последнее дифференциальное уравнение, получаем, что

где С — произвольная постоянная.

Состояние невесомости может быть достигнуто различными способами, хотя оно (вольно или невольно) и ассоциируется с «плаванием» космонавтов в кабине космического корабля.

Рассмотрим горизонтально расположенную балку АВ (рис. 6) постоянного поперечного сечения, сделанную из однородного материала. Ось симметрии балки указана на (рис. 6) пунктирной линией. Предположим, что под влиянием сил, которые действуют на балку в вертикальной плоскости, содержащей ось симметрии, балка прогибается (рис. 7).

Действующие силы могут быть обусловлены весом балки, внешне приложенной нагрузкой или как той, так и другой силами вместе. Понятно, что под действием сил ось симметрии будет искривляться. Обычно искривленную ось симметрии называют упругой линией. Определение формы этой линии играет важную роль в теории упругости.

Отметим, что существуют различные типы балок в зависимости от способов их крепления или опоры. Например, на (рис. 8) изображена балка, у которой конец А жестко закреплен, а конец В свободен. Такая балка называется консольной балкой. На (рис. 9) показана балка, лежащая свободно на опорах А и В. Еще один тип балок с опорами показан па (рис. 10). Существуют и различные способы приложения внешних нагрузок. Например, на (рис. 8) показана равномерно распределенная нагрузка. Конечно, нагрузка может быть и переменной вдоль всей длины балки или некоторой ее части (рис. 9). На (рис. 10) указан случай сосредоточенной нагрузки.

Рассмотрим горизонтальную балку ОА (рис. 11). Пусть ее ось симметрии (показанная на рисунке пунктиром) лежит на оси х, где за положительное направление выбирается направление вправо от точки О, являющейся началом координат. За положительное направление на оси у выберем направление вниз от точки О. Под действием внешних сил F₁, F₂,… (и веса балки, если он большой) ось симметрии искривляется в упругую линию, которая показана на (рис. 12) пунктиром. Смещение y упругой линии от оси х называется прогибом балки в положении х. Таким образом, если известно уравнение упругой линии, то всегда можно указать и прогиб балки. Ниже мы покажем, как это может быть сделано практически.

Обозначим через М(х) изгибающий момент в вертикальном поперечном сечении балки с координатой х. Изгибающий момент определяется как алгебраическая сумма моментов тех сил, которые действуют с одной стороны балки в положении х. При подсчете моментов будем считать, что силы, которые действуют на балку снизу вверх, дают отрицательные моменты, а силы, действующие сверху вниз, дают положительные моменты.

В сопротивлении материалов доказывается, что изгибающий момент в положении х связан с радиусом кривизны упругой линии соотношением

Таким образом, суммарный изгибающий момент в точке Q задается формулой

Как показывают формулы (15) и (16), изгибающие моменты в обоих случаях оказываются равными. Теперь, зная, как находится изгибающий момент, легко выписать и основное уравнение (14), которое в нашем случае принимает вид

Учитывая же, что на концах О и А балка не прогибается, для нахождения у из уравнения (17) воспользуемся условиями на концах балки:

А тогда интегрирование уравнения (17) с учетом последних условий дает

Уравнение (18) является уравнением упругой линии. Формула (18) используется на практике для определения максимального прогиба. Так, в нашем конкретном случае, основываясь на соображениях симметрии (это можно сделать и прямыми вычислениями), находим, что максимальный прогиб будет при х=/2 и равен он 5p 4 /(384EJ) где

Широкое применение дифференциальных уравнений достаточно актуально в современном научном мире. Практически любой процесс может быть описан с помощью дифференциального уравнения.

В данной курсовой работе были рассмотрены пять математических моделей, построенных на основе различных процессов, модель рекламной компании, процесс истечения жидкости из сосудов (водяные часы), кривая погони, невесомость и прогиб балок. Эти модели построены помощью теории дифференциальных уравнений. Задачи, поставленные в курсовой работе, считаем решенными, цель достигнута.

Список используемой литературы

Агафонов С.А., Герман А.Д., Муратова Т.В. Дифференциальные уравнения.

Введение в математическое моделирование Издательства: Университетская книга, Логос, 2007 г.

Амелькин В.В. Дифференциальные уравнения в приложениях. Москва «Наука». Главное издательство физико-математической литературы 1987 г.

Е. Пикуль Математические модели физических процессов Газета «Физика» №12 за 2009 год.

6. Владимиров В.С. «Уравнения математической физики», М., «Наука», 1988 г.

7. И. М Уваренков, М.З. Малер «Курс математического анализа», М., «Просвещение», 1976.

Подобные документы

Дифференциальные уравнения как математический инструмент моделирования и анализа разнообразных явлений и процессов в науке и технике. Описание математических методов решения систем дифференциальных уравнений. Методы расчета токов на участках цепи.

курсовая работа [337,3 K], добавлен 19.09.2011

Дифференциальные уравнения как модели эволюционных процессов. Автономные системы дифференциальных уравнений и их фазовые пространства. Асимптотическая устойчивость линейных однородных автономных систем. Изображения фазовых кривых при помощи ПО Maple.

дипломная работа [477,4 K], добавлен 17.06.2015

Понятия и решения простейших дифференциальных уравнений и дифференциальных уравнений произвольного порядка, в том числе с постоянными аналитическими коэффициентами. Системы линейных уравнений. Асимптотическое поведение решений некоторых линейных систем.

дипломная работа [395,4 K], добавлен 10.06.2010

Установление прямой зависимости между величинами при изучении явлений природы. Свойства дифференциальных уравнений. Уравнения высших порядков, приводящиеся к квадратурам. Линейные однородные дифференциальные уравнения с постоянными коэффициентами.

курсовая работа [209,4 K], добавлен 04.01.2016

Неполные дифференциальные уравнения и их приложения, необходимость их применения в различных областях науки. Понятия и определения, типы и методы решения. Переходная кривая железнодорожного пути. Движение пули внутри вещества. Погружение тел в воду.

курсовая работа [359,4 K], добавлен 29.10.2011

Основные модели естествознания, подходы к исследованию явлений природы, её фундаментальных законов на основе математического анализа. Динамические системы, автономные дифференциальные уравнения, интегро-дифференциальные уравнения, законы термодинамики.

курс лекций [1,1 M], добавлен 02.03.2010

Классификация гиперболических уравнений в общей классификации уравнений математической физики. Классификация уравнений: волновое, интегро-дифференциальные, уравнение теплопроводности. Методы решения в зависимости от видов гиперболических уравнений.

контрольная работа [249,3 K], добавлен 19.01.2009

Существование и единственность решений дифференциальных уравнений. Геометрическая интерпретация решений. Линейные и нелинейные системы. Дифференциальные уравнения, моделирующие динамику популяций конкурирующих видов, их решения и фазовые портреты.

дипломная работа [2,5 M], добавлен 27.06.2012

Анализ динамических процессов в системе на основе использования построенной аналитической модели. Моделирование с использованием пакета расширения Symbolic Math Tolbox. Построение модели в виде системы дифференциальных уравнений, записанных в форме Коши.

курсовая работа [863,4 K], добавлен 21.06.2015

Дифференциальные уравнения Риккати. Общее решение линейного уравнения. Нахождение всех возможных решений дифференциального уравнения Бернулли. Решение уравнений с разделяющимися переменными. Общее и особое решения дифференциального уравнения Клеро.

курсовая работа [347,1 K], добавлен 26.01.2015

Источник