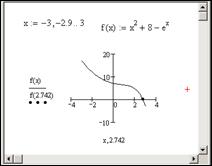
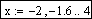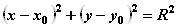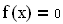В mathcad набрано x 10hy 02o что произойдет если набрать x y
Mathcad Express — бесплатный математический редактор, про который мало кто знает
Прежде всего, приветствую первых посетителей моего блога. Это моя первая статья на Хабре и я надеюсь, что смогу рассказать вам здесь много полезного.
РТС Mathcad – это характерный пример математического ПО, предназначенного для осуществления, как численных, так и аналитических расчетов по формулам и визуализации их результатов в виде графиков. На протяжении последних лет Mathcad стал очень популярным, и его, на мой взгляд, по праву можно считать математическим пакетом №1 в мире.
Сначала несколько фактов о Mathcad, конечно, известных большинству читателей, т.к. Mathcad у нас уже не один десяток лет используется в ВУЗовском обучении, научных и инженерных расчетах. Скорее всего, вы использовали «старую» версию Mathcad (последняя – за номером 15), мало изменившуюся еще с прошлого века. В наши дни она вполне успешно сосуществует с более молодым семейством Mathcad, которое носит имя Mathcad Prime. Таким образом, разработчики несколько лет назад полностью переписали код программы, но заботиться о 100%-й совместимости не стали. Поэтому сейчас они благополучно поддерживают оба семейства – и «старый» Mathcad, и «новый» Mathcad Prime. Дальше и в этой статье, и в моем блоге, будем говорить именно о Mathcad Prime.
Сразу скажу, что русскоязычный дистрибутив, полнофункциональную 30-дневную версию Mathcad Prime вы можете скачать с сайта русского реселлера РТС. Если вы уже собрались попробовать ее в работе, мой совет – не торопитесь в Мастере установки согласиться с включением тестового 30-дневного периода. Дело в том, что Mathcad Prime, наряду с мощной полнофункциональной версией (окно которой вы видите сверху) имеет бесплатную ограниченную версию, которая называется Mathcad Express. Особенность Mathcad Express заключается в том, что большинство функций в этой версии выключено и являются недоступными. Тем не менее, в программе Mathcad Express остается довольно богатый функционал, достаточный, по крайней мере, для того, чтобы изучать математику в школе и на 1-м курсе технического ВУЗа.
Формулы можно вводить в документы либо с клавиатуры (если подходящие символы на ней есть), либо при помощи меню Математика. Давайте ради примера посчитаем интеграл от функции cos(x). Для этого выбираем символ интеграла, а потом — в соответствующие местозаполнители вводим (с клавиатуры) пределы интегрирования и подынтегральную функцию cos(x). Остается нажать клавишу «равно», чтобы сразу получить ответ.
Надо хорошо себе представлять, что происходит, когда мы вводим знак равенства. А именно, запускается соответствующий численный алгоритм вычисления интеграла: интервал интегрирования разбивается на некоторое число отрезков, в определенных точках которых вычисляется массив значений подынтегральной функции, который потом пересчитывается в соответствующую аппроксимацию интегральной суммы. Таким образом, большая часть расчетов скрыта и происходит «за кадром», а на экран выводится лишь конечный результат.
Ключевые инструменты Mathcad – это операторы и функции. Например, в наших расчетах мы использовали оператор интегрирования и функцию косинуса. Для выбора нужной встроенной функции удобно использовать меню Функции.
Давайте теперь определим пользовательскую функцию f(t), которая будет зависеть от переменной t. Будем использовать предназначенный для этого в Mathcad оператор присваивания (двоеточие со знаком равно).
Мы определили функцию f(t), как наш интеграл от cos(x) с переменным верхним пределом t. После того, как мы определили функцию f(t), можно посчитать ее значения в точках (для чего достаточно ввести аргумент и нажать клавишу «равно», чтобы вывести в документ ответ). Для ввода константы, например π, используется или меню Символы, или меню Константы.
В качестве аргумента можно использовать не только скалярную, но и векторную переменную. Определить ее можно так:
Тогда и результатом вычисления функции будет соответствующий вектор.
Наконец, одна из важных возможностей Mathcad Express – это возможность построения в документе графиков. Давайте выделим место в документе и вставим в это место XY-график (т.е. декартов график) нашей функции f(x).
Обозначаем на оси абсцисс имя переменной z (чтобы не путать с уже использованными ранее x и t), а на оси ординат – имя функции f(z), функцию, которую, как вы помните, мы определили, как интеграл от косинуса, равный конечно, sin(z). В итоге, получаем график этой функции.
Скажу еще, что в Mathcad Express (возможно, по недосмотру разработчика) остаются доступными матричные операции. Поэтому Mathcad Express — довольно мощный инструмент для решения задач линейной алгебры.
Переходя по документу вверх и вниз, мы можем просматривать свои расчеты, а управлять ими можно при помощи меню Расчет. По умолчанию, включена опция автоматического расчета (по мере ввода формул в документ, эти формулы сразу рассчитываются). Если эту опцию отключить, то для того чтобы рассчитать документ вручную, достаточно нажить кнопку Рассчитать.
Давайте я на этом остановлюсь, полагая, что задача знакомства читателя с Mathcad Express решена, и в следующих статьях блога, когда речь пойдет, собственно, о математике, я смогу использовать расчеты в Mathcad, не углубляясь в его интерфейс.
В заключение, адресую заинтересовавшегося читателя к своему видеокурсу по математическому анализу, который в формате МООС прошел на портале ИНТУИТ в 2014 году. Все лабораторные работы выполнены в Mathcad Prime и скачать их можно здесь. Все эти материалы на сайте Nerepetitor.ru бесплатные, регистрация не требуется.
В mathcad набрано x 10hy 02o что произойдет если набрать x y
Mathcad дает возможность решать также и системы уравнений. Максимальное число уравнений и переменных равно пятидесяти. В первой части этого раздела описаны процедуры решения систем уравнений. В заключительной части приведены примеры и проведено обсуждение некоторых часто встречающихся ошибок. Результатом решения системы будет численное значение искомого корня. Для символьного решения уравнений необходимо использовать блоки символьного решения уравнений. При символьном решении уравнений искомый корень выражается через другие переменные и константы.
Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое-либо выражение, содержащее функцию Find, называются блоком решения уравнений.
На Рисунке 5 показан рабочий документ, который использует блок решения уравнений для решения одного уравнения с одним неизвестным. Так как имеется только одно уравнение, то только одно уравнение появляется между ключевым словом Given и формулой, включающей функцию Find. Так как уравнение имеет одно неизвестное, то функция Find имеет только один аргумент. Для решения одного уравнения с одним неизвестным можно также использовать функцию root, как показано ниже:
Рисунок 5: Блок решения уравнений для одного уравнения с одним неизвестным.
Между ключевым словом Given и функцией Find в блоке решения уравнений могут появляться выражения строго определенного типа. Ниже приведен список всех выражений, которые могут быть использованы в блоке решения уравнений. Использование других выражений не допускается. Эти выражения часто называются ограничениями. В таблице, приведенной ниже, через x и y обозначены вещественнозначные скалярные выражения, а через z и w обозначены любые скалярные выражения.
| Условие | Как ввести | Описание |
| w = z | [Ctrl] = | Булево равенство возвращает 1, если операнды равны; иначе 0 |
| x > y | > | Больше чем. |
| x |
Что делать, когда имеется слишком мало ограничений
Если количество ограничений меньше, чем количество переменных, Mathcad вообще не может выполнить блок решения уравнений. Mathcad помечает в этом случае функцию Find сообщением об ошибке “слишком мало ограничений”.
Задача, аналогичная той, которая приведена на Рисунке 12, называется недоопределенной. Ограничений в ней меньше, чем переменных. Поэтому ограничения не содержат достаточной информации для поиска решения. Поскольку функция Find имеет пять аргументов, Mathcad определяет, что требуется решить два уравнения с пятью неизвестными. Вообще говоря, такая задача обычно имеет бесконечное число решений.
При использовании блока решения уравнений в Mathcad необходимо задать количество уравнений по крайней мере не меньшее, чем число искомых неизвестных. Если зафиксировать значения некоторых переменных, удастся решить уравнения относительно оставшихся переменных. На Рисунке 13 показано, как, зафиксировав часть переменных, решить недоопределенную задачу из Рисунка 12. Поскольку функция Find содержит только два аргумента, z и w, Mathcad определяет переменные x, y и v как имеющие фиксированные значения 10, 50 и 0 соответственно. Блок решения уравнений становится в этом случае корректно определенным, потому что теперь имеются только две неизвестных, z и w, и два уравнения.
Рисунок 12: Функция Find имеет пять аргументов, поэтому Mathcad определяет, что требуется решить два уравнения с пятью неизвестными.
Рисунок 13: Проблема может быть решена, если уменьшить количество аргументов функции Find.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
В mathcad набрано x 10hy 02o что произойдет если набрать x y
БАЗОВЫЕ ОПЕРАЦИИ.
РАНЖИРОВАННЫЕ ПЕРЕМЕННЫЕ. ФУНКЦИИ. ГРАФИКИ
МАССИВЫ
1 Запуск. Формульные и текстовые области
Запуск Mathcad: Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
Документ Mathcad просматривается, интерпретируется и выполняется слева направо и сверху вниз и может включать три вида областей:
Для ввода математических символов: View / Toolbars / Math (Вид / Панели инструментов / Математическая).
Каждое математическое выражение набирается в отдельной формульной области. Одна формула – одна область!
Для вставки в документ текстовой области выполняют Insert / Text Region (Вставка / Область текста), либо просто нажимают в формульной области Пробел. Текстовая область имеет рамку с маркерами, позволяющими изменять ее размеры, и курсор в виде вертикальной линии красного цвета.
2 Ранжированные переменные. Функции. Графики
В Mathcad существует тип переменных, принимающих не одно, а множество значений. Такие переменные носят название ранжированных или дискретных. Ранжированная переменная – переменная, которая принимает ряд значений при каждом ее использовании, причем каждое значение отличается от соседнего на постоянную величину, называемую шагом.
Ранжированная переменная общего вида определяется выражением:
Например, если переменная изменяется в интервале 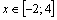
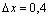
Шаг изменения значений ранжированной переменной в явном виде обычно не задается, он определяется как x2 – x1.
Функции в системе Mathcad можно условно разделить на две группы: встроенные и функции пользователя. Встроенные функции изначально заданы в системе разработчиками. Имя функции вводится с клавиатуры, обычно в нижнем регистре. Полный перечень встроенных функций можно получить, выполнив команду Function (Функция) главного меню Insert (Вставка), или нажав на кнопку 
Среди наиболее часто используемых функций можно указать:
Функция пользователя сначала должна быть определена, а затем к ней можно обращаться при вычислениях, записи алгебраических выражений, построении графиков и т. п. Функция пользователя определяется
Имя(список аргументов) := Выражение
Сначала задается имя функции, в круглых скобках указывается список аргументов функции (перечень используемых переменных), разделяемых запятыми. Затем вводится оператор присваивания. Справа от него записывается выражение, содержащее доступные системе операторы, операнды и функции с аргументами, указанными в списке аргументов.
Обращение к функции осуществляется по ее имени с подстановкой на место аргументов констант, переменных, определенных до обращения к функции, и выражений.
Основные виды графиков и инструменты для работы с ними находятся на палитре математических инструментов Graph (График).
Для построения графика функции одной переменной в декартовой системе координат в Mathcad:
Массив в пакете Mathcad – это совокупность конечного числа упорядоченных пронумерованных элементов, которая может иметь уникальное имя. Обычно используют одномерные (векторы) и двумерные (матрицы) массивы, содержащие числовые, символьные или строковые данные.

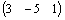
Порядковый номер элемента называется индексом. Местоположение элемента в массиве задается одним индексом для вектора и двумя – для матрицы. Номер первого элемента массива определяется значением системной переменной ORIGIN. По умолчанию ORIGIN = 0 и может принимать только целые значения. Изменение значения этой системной переменной осуществляется последовательностью команд Math / Options… / Built-In Variables / Array Origin (ORIGIN) (Математика / Параметры / Встроенные переменные / Начальный индекс массивов) или переопределением в документе, например:
Существует несколько способов создания массивов.
1-й способ. Использование панели Matrix (Матрицы).
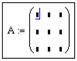
Сначала набирается имя массива и оператор присваивания, например, 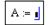
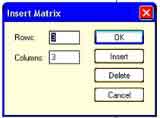
Далее указываем количество ее строк m (Rows) и столбцов n (Columns) матрицы. Для векторов один из этих параметров должен быть равен 1. При m = 1 получим вектор-строку, а при n = 1 – вектор-столбец.
На месте курсора появится шаблон, в знакоместа которого вводятся значения элементов массива:
2-й способ. Использование ранжированной переменной.
Целочисленные ранжированные переменные используются для задания индексов и позволяют создавать массивы в следующем порядке:
Обращаться к отдельным элементам вектора или матрицы можно, используя нижний индекс, принимающий только целочисленные значения. Для ввода нижнего индекса после имени вектора или матрицы нажимается клавиша «[» (прямая открывающая скобка) либо используется пиктограмма 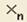
Для работы с векторами и матрицами система Mathcad имеет ряд специальных операторов и команд (представленных в таблице 1), используя которые не следует забывать об общих правилах матричного исчисления.
Таблица 1 – Команды палитры инструментов Matrix (Матрица)
Математика : Учебное пособие: Пособие MathCAD
1. Рабочее окно MathCAD
· Панель Математика (рис. 1.4).
Рис. 1.4. Панель Математика
При щелчке на кнопке математической панели инструментов открывается дополнительная панель:






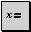

2. Элементы языка MathCAD
К основным элементам математических выражений MathCAD относятся операторы, константы, переменные, массивы и функции.
Операторы — элементы MathCAD, с помощью которых можно создавать математические выражения. К ним, например, относятся символы арифметических операций, знаки вычисления сумм, произведений, производной, интеграла и т.д.
а) действие, которое должно выполняться при наличии тех или иных значений операндов;
б) сколько, где и какие операнды должны быть введены в оператор.
Операнд — число или выражение, на которое действует оператор. Например, в выражении 5!+3 числа 5! и 3 — операнды оператора «+» (плюс), а число 5 — операнд факториала (!).
Любой оператор в MathCAD можно ввести двумя способами:
· нажав клавишу (сочетание клавиш) на клавиатуре;
· используя математическую панель.
Для присвоения или вывода содержимого ячейки памяти, связанной с переменной, используются следующие операторы:
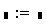
Такое присвоение называется локальным. До этого присваивания переменная не определена и ее нельзя использовать.
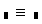

= — оператор (простое равно), отведенный для вывода значения константы или переменной.
Процесс вычисления осуществляется при помощи:


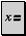
Внимание. Если необходимо поделить все выражение в числителе, то его нужно первоначально выделить, нажав пробел на клавиатуре или поместив в скобки.
Константы — поименованные объекты, хранящие некоторые значения, которые не могут быть изменены.
Размерные константы — это общепринятые единицы измерения. Например, метры, секунды и т.д.
Чтобы записать размерную константу, необходимо после числа ввести знак * (умножить), выбрать пункт меню Вставка подпункт Юнит. В измерениях наиболее известные вам категории: Length — длина (м, км, см); Mass — вес (гр, кг, т); Time — время (мин, сек, час).
Переменные являются поименованными объектами, имеющими некоторое значение, которое может изменяться по ходу выполнения программы. Переменные могут быть числовыми, строковыми, символьными и т.д. Значения переменным задаются с помощью знака присвоить (: =).
Внимание. MathCAD прописные и строчные буквы воспринимает как разные идентификаторы.
В MathCAD содержится небольшая группа особых объектов, которые нельзя отнести ни к классу констант, ни к классу переменных, значения которых определены сразу после запуска программы. Их правильнее считать системными переменными. Это, например, TOL [0.001]- погрешность числовых расчетов, ORIGIN [0] — нижняя граница значения индекса индексации векторов, матриц и др. Значения этим переменным при необходимости можно задать другие.
Эти переменные имеют ряд фиксированных значений, либо целочисленных, либо изменяющихся с определенным шагом от начального значения до конечного.
Для создания ранжированной переменной используется выражение:
где Name — имя переменной;
Nbegin — начальное значение;
Step — заданный шаг изменения переменной;
Nend — конечное значение.
Ранжированные переменные широко применяются при построении графиков. Например, для построения графика некоторой функции f(x) прежде всего необходимо создать ряд значений переменной x — для этого она должна быть ранжированной переменной.
Внимание. Если в диапазоне изменения переменной не указывать шаг, то программа автоматически примет его равным 1.
Пример. Переменная x изменяется в диапазоне от –16 до +16 с шагом 0.1
Чтобы записать ранжированную переменную, нужно ввести:
— первое значение диапазона (–16);
— второе значение диапазона, которое является суммой первого значения и шага (–16+0.1);
— многоточие (..) изменение переменной в заданных пределах (многоточие вводится нажатием точки с запятой в английской раскладке клавиатуры);
— последнее значение диапазона (16).
В результате у вас получится: x := –16,–16+0.1..16.
Любое выражение с ранжированными переменными после знака равенства инициирует таблицу вывода.
В таблицы вывода можно и вставлять числовые значения и корректировать их.
Переменная с индексом
Переменная с индексом — это переменная, которой присвоен набор не связанных друг с другом чисел, каждое из которых имеет свой номер (индекс).
Ввод индекса осуществляется нажатием левой квадратной скобки на клавиатуре или при помощи кнопки xn на панели Калькулятор.
В качестве индекса можно использовать как константу, так и выражение. Для инициализации переменной с индексом необходимо ввести элементы массива, разделяя их запятыми.
Пример. Ввод индексных переменных.
i:= 0..2 — индекс изменяется от 0 до 2 (индексная переменная будет содержать 3 элемента).
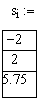
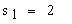
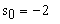
Массив — имеющая уникальное имя совокупность конечного числа числовых или символьных элементов, упорядоченных некоторым образом и имеющих определенные адреса.
В пакете MathCAD используются массивы двух наиболее распространенных типов:
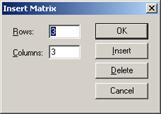
Вывести шаблон матрицы или вектора можно одним из способов:
· нажать комбинацию клавиш Ctrl + M;
· нажать кнопку 
В результате появится диалоговое окно, в котором задается необходимое число строк и столбцов:
Columns — число столбцов
Если матрице (вектору) нужно присвоить имя, то вначале вводится имя матрицы (вектора), затем оператор присвоения и после — шаблон матрицы.

Матрица — двухмерный массив с именем Мn,m, состоящий из n строк и m столбцов.
С матрицами можно выполнять различные математические операции.
Функция — выражение, согласно которому производятся некоторые вычисления с аргументами и определяется его числовое значение. Примеры функций: sin(x), tan(x) и др.
Функции в пакете MathCAD могут быть как встроенными, так и определенными пользователем. Способы вставки встроенной функции:
· Выбрать пункт меню Вставка – Функция.
· Нажать комбинацию клавиш Ctrl + E.
· 
· Набрать имя функции на клавиатуре.
Функции пользователя обычно используются при многократных вычислениях одного и того же выражения. Для того чтобы задать функцию пользователя необходимо:
· ввести имя функции с обязательным указанием в скобках аргумента, например, f(x);
· ввести оператор присвоения (:=);
· ввести вычисляемое выражение.
3. Форматирование чисел
В MathCAD можно изменить формат вывода чисел. Обычно вычисления производятся с точностью 20 знаков, но выводятся на экран не все значащие цифры. Чтобы изменить формат числа, необходимо дважды щелкнуть на нужном численном результате. Появится окно форматирования чисел, открытое на вкладке Number Format (Формат чисел) со следующими форматами:
o General (Основной) — принят по умолчанию. Числа отображаются с порядком (например, 1.22´105). Число знаков мантиссы определяется в поле Exponential Threshold (Порог экспоненциального представления). При превышении порога число отображается с порядком. Число знаков после десятичной точки меняется в поле Number of decimal places.
o Decimal (Десятичный) — десятичное представление чисел с плавающей точкой (например, 12.2316).
o Scientific (Научный) — числа отображаются только с порядком.
o Engineering (Инженерный) — числа отображаются только с порядком, кратным трем (например, 1.22´106).
Внимание. Если после установления нужного формата в окне форматирования чисел выбрать кнопку Ок, формат установится только для выделенного числа. А если выбрать кнопку Set as Default, формат будет применен ко всем числам данного документа.
Автоматически числа округляются до нуля, если они меньше установленного порога. Порог устанавливается для всего документа, а не для конкретного результата. Для того чтобы изменить порог округления до нуля, необходимо выбрать пункт меню Форматирование Результат и во вкладке Tolerance, в поле Zero threshold ввести необходимое значение порога.
Текстовые фрагменты представляют собой куски текста, которые пользователь хотел бы видеть в своем документе. Это могут быть пояснения, ссылки, комментарии и т.д. Они вставляются при помощи пункта меню Вставка – Текстовый регион.
Вы можете отформатировать текст: поменять шрифт, его размер, начертание, выравнивание и т.д. Для этого нужно его выделить и выбрать соответствующие параметры на панели шрифтов или в меню Форматирование – Текст.
5. Работа с графикой
При решении многих задач, где производится исследование функции, часто возникает необходимость в построении ее графика, где наглядно будет отражено поведение функции на определенном промежутке.
В системе MathCAD существует возможность построения различных видов графиков: в декартовой и полярной системе координат, трехмерных графиков, поверхностей тел вращения, многогранников, пространственных кривых, графиков векторного поля. Мы рассмотрим приемы построения некоторых из них.
5.1 Построение двухмерных графиков
Для построения двухмерного графика функции необходимо:
· задать диапазон значений аргумента;
· установить курсор в то место, где должен быть построен график, на математической панели выбрать кнопку Graph (график) и в открывшейся панели кнопку X-Y Plot (двухмерный график);
· в появившемся шаблоне двухмерного графика, представляющем собой пустой прямоугольник с метками данных, в центральную метку данных по оси абсцисс (ось X) ввести имя переменной, а на месте центральной метки данных по оси ординат (ось Y) ввести имя функции (рис. 2.1);\
Рис. 2.1. Шаблон двухмерного графика
щелкнуть мышью вне шаблона графика — график функции будет построен.
Диапазон изменения аргумента состоит из 3-х значений: начальное, второе и конечное.
Пусть необходимо построить график функции на интервале [-2,2] с шагом 0.2. Значения переменной t задаются в виде диапазона следующим образом:
где: –2 — начальное значение диапазона;
–1.8 (–2 + 0.2) — второе значение диапазона (начальное значение плюс шаг);
2 — конечное значение диапазона.
Внимание. Многоточие вводится нажатием точки с запятой в английской раскладке клавиатуры.
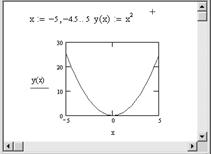
Пример. Построение графика функции y = x2 на интервале [–5,5] с шагом 0.5 (рис. 2.2).
Рис. 2.2. Построение графика функции y = x2
При построении графиков необходимо учитывать следующее:
° Если диапазон значений аргумента не задан, то по умолчанию график строится в диапазоне [–10,10].
° Если в одном шаблоне необходимо разместить несколько графиков, то имена функций указываются через запятую.
° Если две функции имеют различные аргументы, например f1(x) и f2(y), то на оси ординат (Y) через запятую указываются имена функций, а по оси абсцисс (X) имена обеих переменных тоже через запятую.
° Крайние метки данных на шаблоне графика служат для указания предельных значений абсцисс и ординат, т.е. они задают масштаб графика. Если оставить эти метки незаполненными, то масштаб будет установлен автоматически. Автоматический масштаб не всегда отражает график в нужном виде, поэтому предельные значения абсцисс и ординат приходится редактировать, изменяя вручную.
Примечание. Если после построения график не принимает нужный вид, можно:
· изменить интервал построения графика.
· уменьшить на графике предельные значения абсцисс и ординат.
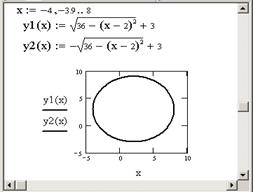
Пример. Построение окружности с центром в точке (2,3) и радиусом R = 6.
Уравнение окружности с центром в точке с координатами (x0,y0) и радиусом R записывается в виде:
Выразим из этого уравнения y:
Таким образом, для построения окружности необходимо задать две функции: верхнюю и нижнюю полуокружности. Диапазон значений аргумента вычисляется следующим образом:
— начальное значение диапазона = x0 – R;
— конечное значение диапазона = x0 + R;
— шаг лучше взять равным 0.1 (рис. 2.3.).
Рис. 2.3. Построение окружности
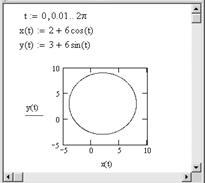
Параметрический график функции
Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты x и y, рассматривать так называемые параметрические уравнения линии, дающие выражения текущих координат x и y в виде функций от некоторой переменной величины t (параметра): x(t) и y(t). При построении параметрического графика на осях ординат и абсцисс указываются имена функций одного аргумента.
Пример. Построение окружности с центром в точке с координатами (2,3) и радиусом R = 6. Для построения используется параметрическое уравнение окружности
Рис.2.4. Построение окружности
Чтобы отформатировать график, необходимо дважды щелкнуть по области графика. Откроется диалоговое окно форматирования графика. Ниже перечислены вкладки окна форматирования графика:
— X—Y Axes — форматирование осей координат. Установив нужные флажки можно:
· Log Scale — представить численные значения на осях в логарифмическом масштабе (по умолчанию численные значения наносятся в линейном масштабе)
· Grid Lines — нанести сетку линий;
· Numbered — расставить числа по координатным осям;
· Auto Scale — автоматический выбор предельных численных значений на осях (если этот флажок снят, предельными будут максимальные вычисленные значения);
· Show Marker — нанесение меток на график в виде горизонтальных или вертикальных пунктирных линий, соответствующих указанному значению на оси, причем сами значения выводятся в конце линий (на каждой оси появляются 2 места ввода, в которые можно ввести численные значения, не вводить ничего, ввести одно число или буквенные обозначения констант);
· Auto Grid — автоматический выбор числа линий сетки (если этот флажок снят, надо задать число линий в поле Number of Grids);
· Crossed — ось абсцисс проходит через нуль ординаты;
· Boxed — ось абсцисс проходит по нижнему краю графика.
— Trace — форматирование линии графиков функций. Для каждого графика в отдельности можно изменить:
· символ (Symbol) на графике для узловых точек (кружок, крестик, прямоугольник, ромб);
· вид линии (Solid — сплошная, Dot — пунктир, Dash — штрихи, Dadot штрих-пунктир);
· тип (Туре) графика (Lines — линия, Points — точки, Ваr или Solidbar — столбики, Step — ступенчатый график и т.д.);
· толщину линии (Weight).
— Label — заголовок в области графика. В поле Title (Заголовок) можно записать текст заголовка, выбрать его положение — вверху или внизу графика (Above вверху, Below — внизу). Можно вписать, если надо, названия аргумента и функции (Axis Labels).
— Defaults — с помощью этой вкладки можно вернуться к виду графика, принятому по умолчанию (Change to default), либо сделанные вами изменения на графике использовать по умолчанию для всех графиков данного документа (Use for Defaults).
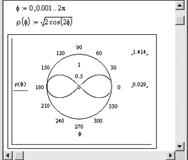
5.2 Построение полярных графиков
Для построения полярного графика функции необходимо:
· задать диапазон значений аргумента;
· установить курсор в то место, где должен быть построен график, на математической панели выбрать кнопку Graph (график) и в открывшейся панели кнопку Polar Plot (полярный график);
· в местах ввода появившегося шаблона необходимо ввести угловой аргумент функции (внизу) и имя функции (слева).
Пример. Построение лемнискаты Бернулли: 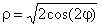

Рис.2.6. Пример построения полярного графика
5.3 Построение графиков поверхностей (трехмерные или 3D-графики)
При построении трехмерных графиков используется панель Graph (График) математической панели. Можно построить трехмерный график с помощью мастера, вызываемого из главного меню; можно построить график, создав матрицу значений функции двух переменных; можно задействовать ускоренный метод построения; можно вызвать специальные функции CreateMech и CreateSpase, предназначенные для создания массива значений функции и построения графика. Мы рассмотрим ускоренный метод построения трехмерного графика.
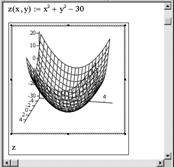
Быстрое построение графика
Для быстрого построения трехмерного графика функции необходимо:
· установить курсор в то место, где должен быть построен график, на математической панели выбрать кнопку Graph (График) и в открывшейся панели кнопку 
· в единственное место шаблона введите имя функции (не указывая переменные);
· щелкнуть мышью вне шаблона графика — график функции будет построен.
Пример. Построение графика функции z(x,y) = x2 + y2 – 30 (рис. 2.7).
Рис. 2.7. Пример быстрого построения поверхностного графика
Построенным графиком можно управлять:
° вращение графика выполняется после наведения на него указателя мыши при нажатой левой кнопке мыши;
° масштабирование графика выполняется после наведения на него указателя мыши при одновременном нажатии левой кнопки мыши и клавиши Ctrl (если двигать мышь, график приближается или удаляется);
° анимация графика выполняется аналогично, но при нажатой дополнительно клавише Shift. Необходимо только начать вращение графика мышью, дальше анимация будет выполняться автоматически. Для остановки вращения следует щелкнуть левой кнопкой мыши внутри области графика.
Существует возможность построения сразу нескольких поверхностей на одном рисунке. Для этого необходимо задать обе функции и через запятую указать имена функций на шаблоне графика.
При быстром построении графика по умолчанию выбираются значения обоих аргументов в пределах от –5 до +5 и число контурных линий, равное 20. Для изменения этих значений необходимо:
· дважды щелкнуть по графику;
· в открывшемся окне выбрать вкладку Quick Plot Data;
· ввести новые значения в области окна Range1 для первого аргумента и Range2 для второго аргумента (start начальное значение, end — конечное значение);
· в поле # of Grids изменить число линий сетки, покрывающих поверхность;
· щелкнуть на кнопке Ок.
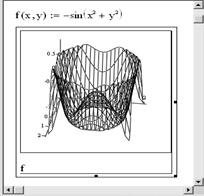
Пример. Построение графика функции z(x,y) = –sin(x2 + y2) (рис. 2.9).
При построении этого графика пределы изменения значений обоих аргументов лучше выбрать от –2 до +2.
Рис. 2.9. Пример построения графика функции z(x,y) = –sin(x2 + y2)
Форматирование трехмерных графиков
Для форматирования графика необходимо дважды щелкнуть по области построения появится окно форматирования с несколькими вкладками: Appearance, General, Axes, Lighting, Title, Backplanes, Special, Advanced, Quick Plot Data.
Назначение вкладки Quick Plot Data было рассмотрено выше.
Вкладка Appearance позволяет менять внешний вид графика. Поле Fill Options позволяет изменить параметры заливки, поле Line Option — параметры линий, Point Options — параметры точек.
Во вкладке General (общие) в группе View можно выбрать углы поворота изображенной поверхности вокруг всех трех осей; в группе Display as можно поменять тип графика.
Во вкладке Lighting (освещение) можно управлять освещением, установив флажок Enable Lighting (включить освещение) и переключатель On (включить). Одна из 6-ти возможных схем освещения выбирается в списке Lighting scheme (схема освещения).
6. Способы решения уравнений в MathCAD
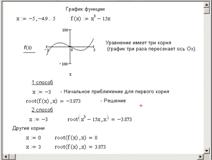
В данном разделе мы узнаем, каким образом в системе MathCAD решаются простейшие уравнения вида F(x) = 0. Решить уравнение аналитически — значит найти все его корни, т.е. такие числа, при подстановке которых в исходное уравнение получим верное равенство. Решить уравнение графически — значит найти точки пересечения графика функции с осью ОХ.
6.1 Решение уравнений с помощью функции root(f(x),x)
Для решений уравнения с одним неизвестным вида F(x) = 0 существует специальная функция
где f(x) выражение, равное нулю;
Эта функция возвращает с заданной точностью значение переменной, при котором выражение f(x) равно 0.
Внимание. Если правая часть уравнения ¹0, то необходимо привести его к нормальному виду (перенести все в левую часть).
Перед использованием функции root необходимо задать аргументу х начальное приближение. Если корней несколько, то для отыскания каждого корня необходимо задавать свое начальное приближение.
Внимание. Перед решением желательно построить график функции, чтобы проверить, есть ли корни (пересекает ли график ось Ох), и если есть, то сколько. Начальное приближение можно выбрать по графику поближе к точке пересечения.
Пример. Решение уравнения 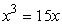
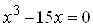
Рис. 3.1. Решение уравнения при помощи функции root
6.2 Решение уравнений с помощью функции Polyroots(v)
Для одновременного нахождения всех корней полинома используют функцию Polyroots(v), где v — вектор коэффициентов полинома, начиная со свободного члена. Нулевые коэффициенты опускать нельзя. В отличие от функции root функция Polyroots не требует начального приближения.
Пример. Решение уравнения 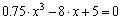
Рис. 3.2. Решение уравнения с помощью функции polyroots
Функция Find (Найти) работает в ключевой связке с ключевым словом Given (Дано). Конструкция Given – Find использует расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.
Если задано уравнение f(x) = 0, то его можно решить следующим образом с помощью блока Given – Find:
– задать начальное приближение
– ввести служебное слово
– записать уравнение, используя знак жирное равно
– написать функцию find с неизвестной переменной в качестве параметра
В результате после знака равно выведется найденный корень.
Если существует несколько корней, то их можно найти, меняя начальное приближение х0 на близкое к искомому корню.
Пример. Решение уравнения 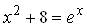
Рис. 3.3. Решение уравнения с помощью функции find
Иногда возникает необходимость отметить на графике какие-либо точки (например, точки пересечения функции с осью Ox). Для этого необходимо:
· указать значение x данной точки (по оси Ох) и значение функции в этой точке (по оси Оy);
· дважды щелкнуть по графику и в окне форматирования во вкладке Traces для соответствующей линии выбрать тип графика — points, толщину линии — 2 или 3.
Пример. На графике отмечена точка пересечения функции 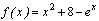
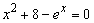
Рис. 3.4. График функции 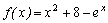
В окне форматирования графика во вкладке Traces для trace2 изменены: тип графика — points, толщина линии — 3, цвет — черный.
7. Решение систем уравнений
7.1 Решение систем линейных уравнений
Систему линейных уравнений можно решить матричным методом (или через обратную матрицу или используя функцию lsolve(A,B)) и с использованием двух функций Find и функции Minerr.
Пример. Дана система уравнений:
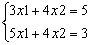
Решение данной системы уравнений матричным методом представлено на рисунке 4.1.
Рис. 4.1. Решение системы линейных уравнений матричным методом
Lsolve(A,B) — это встроенная функция, которая возвращает вектор Х для системы линейных уравнений 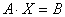
Пример. Дана система уравнений:
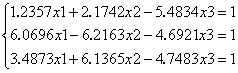
Способ решения данной системы с использованием функции lsolve(A,B) приведен на рисунке 4.2.
Рис. 4.2. Решение системы линейных уравнений с использованием функции lsolve
Решение системы линейных уравнений с помощью функции Find
При данном методе уравнения вводятся без использования матриц, т.е. в «натуральном виде». Предварительно необходимо указать начальные приближения неизвестных переменных. Это могут быть любые числа, входящие в область определения. Часто за них принимают столбец свободных членов.
Для того чтобы решить систему линейных уравнений с помощью вычислительного блока Given – Find, необходимо:
1) задать начальные приближения для всех переменных;
2) ввести служебное слово Given;
3) записать систему уравнений, используя знак жирное равно(=);
4) написать функцию Find, перечислив неизвестные переменные в качестве параметров функции.
В результате расчетов выведется вектор решения системы.
Пример. Дана система уравнений:
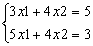
Решение данной системы с помощью вычислительного блока Given – Find приведено на рисунке 4.3.
Рис. 4.3. Решение системы линейных уравнений с помощью функции Find
Приближенное решение системы линейных уравнений
Решение системы линейных уравнений с помощью функцию Minerr аналогично решению с помощью функции Find (используется тот же алгоритм), только функция Find дает точное решение, а Minerr — приближенное. Если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, Minerr возвращает это приближение. Функция Find в этом случае возвращает сообщение об ошибке.
Общие рекомендации по решению уравнений и систем уравнений
Ниже перечислены некоторые рекомендации, которые следует выполнять, если MathCAD не может самостоятельно найти решение.
· Можно подобрать другое начальное приближение.
· Можно увеличить или уменьшить точность расчетов. Для этого в меню выбрать Math ► Options (Математика – Опции), вкладка Built—In Variables (Встроенные переменные). В открывшейся вкладке необходимо уменьшить допустимую погрешность вычислений (Convergence Tolerance (TOL)). По умолчанию TOL = 0.001.
Внимание. При матричном методе решения необходимо переставить коэффициенты согласно возрастанию неизвестных х1, х2, х3, х4.
7.2 Решение систем нелинейных уравнений
Системы нелинейных уравнений в MathCAD решаются с помощью вычислительного блока Given – Find.
Конструкция Given – Find использует расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.
Для решения системы уравнений с помощью блока Given – Find необходимо:
1) задать начальные приближения для всех переменных;
2) ввести служебное слово Given;
3) записать систему уравнений, используя знак жирное равно(=);
4) написать функцию Find, перечислив неизвестные переменные в качестве параметров функции.
В результате расчетов выведется вектор решения системы.
Если система имеет несколько решений, алгоритм следует повторить с другими начальными приближениями.
Примечание. Если решается система из двух уравнений с двумя неизвестными, перед решением желательно построить графики функций, чтобы проверить, есть ли корни у системы (пересекаются ли графики заданных функций), и если есть, то сколько. Начальное приближение можно выбрать по графику поближе к точке пересечения.
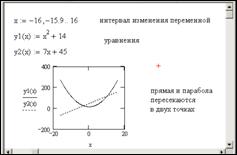
Пример. Дана система уравнений
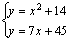
Перед решением системы построим графики функций: параболы (первое уравнение) и прямой (второе уравнение). Построение графика прямой и параболы в одной системе координат приведено на рисунке 4.5:
Рис. 4.5. Построение графика двух функций в одной системе координат
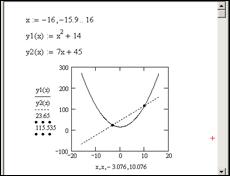
Прямая и парабола пересекаются в двух точках, значит, система имеет два решения. По графику выбираем начальные приближения неизвестных x и y для каждого решения. Нахождение корней системы уравнений представлено на рисунке 4.6.
Рис. 4.6. Нахождение корней системы нелинейных уравнений
Для того чтобы отметить на графике точки пересечения параболы и прямой, координаты точек, найденные при решении системы, введем по оси Ох (значения х) и по оси Оу (значения у) через запятую. В окне форматирования графика во вкладке Traces для trace3 и trace4 изменим: тип графика — points, толщина линии — 3, цвет — черный (рис. 4.7).
Рис. 4.7. Графики функций с отмеченными точками пересечения
8. Примеры использования основных возможностей MathCAD для решения некоторых математических задач
В данном разделе приведены примеры решения задач, для решения которых необходимо решить уравнение или систему уравнений.
8.1 Нахождение локальных экстремумов функций
Необходимое условие экстремума (максимума и/или минимума) непрерывной функции формулируется так: экстремумы могут иметь место только в тех точках, где производная или равна нулю, или не существует (в частности, обращается в бесконечность). Для нахождения экстремумов непрерывной функции сначала находят точки, удовлетворяющие необходимому условию, то есть находят все действительные корни уравнения 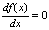
Если построен график функции, то можно сразу увидеть — максимум или минимум достигается в данной точке х. Если графика нет, то каждый из найденных корней исследуют одним из способов.
2-й способ. Вычисление второй производной. В этом случае вычисляется вторая производная 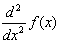
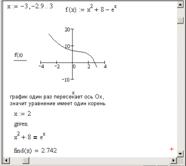
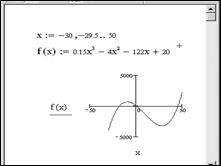
Пример. Нахождение экстремумов (минимумов/максимумов) функции 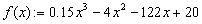
Сначала построим график функции (рис. 6.1).
Рис. 6.1. Построение графика функции
Определим по графику начальные приближения значений х, соответствующих локальным экстремумам функции f(x). Найдем эти экстремумы, решив уравнение 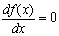
Рис. 6.2. Нахождение локальных экстремумов
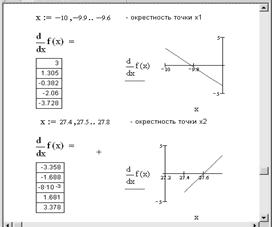
Определим вид экстремумов первым способом, исследуя изменение знака производной в окрестности найденных значений (рис. 6.3).
Рис. 6.3. Определение вида экстремума
Из таблицы значений производной и из графика видно, что знак производной в окрестности точки x1 меняется с плюса на минус, поэтому в этой точке функция достигает максимума. А в окрестности точки x2 знак производной поменялся с минуса на плюс, поэтому в этой точке функция достигает минимума.
Определим вид экстремумов вторым способом, вычисляя знак второй производной (рис. 6.4).
Рис. 6.4. Определение вида экстремума с помощью второй производной
Видно, что в точке x1 вторая производная меньше нуля, значит, точка х1 соответствует максимуму функции. А в точке x2 вторая производная больше нуля, значит, точка х2 соответствует минимуму функции.
Площадь криволинейной трапеции, ограниченной графиком функции f(x), отрезком [a,b] на оси Ox и двумя вертикалями х = а и х = b, a