Основная теорема матричных игр

Основная теорема матричных игр (теорема Д. фон Неймана) утверждает, что каждая конечная игра имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий, то есть всегда имеет место равенство

(4.2.1)

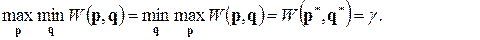
Смешанные стратегии и , удовлетворяющие равенству (4.2.1) называют оптимальными(они образуют ситуацию равновесия), а величину γ―средний результат игры при использовании оптимальных смешанных стратегий называют ценой игры.

Если оба игрока используют свои оптимальные смешанные стратегии, то

(4.2.2)

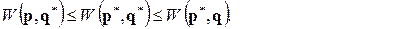
Для того, чтобы в матричной игреситуацияв смешанных стратегиях и была ситуацией равновесия, необходимо и достаточно, чтобы условие (4.2.2) выполнялось не для всех возможных смесей активных чистых стратегий, а только для всех чистых стратегий игроков 1 и 2.

Если один из игроков использует свою оптимальную смешанную стратегию, то его средний выигрыш(проигрыш) остается неизменным и равным цене игры γ независимо от того, какой смесью активных чистых стратегий пользуется другой игрок.

В частности, средний выигрыш игрока 1 (средний проигрыш игрока 2) остается неизменным и равным цене игры γ при использовании игроком 2 (игроком 1) любой чистой стратегии.

Докажем это для игры m×n. Пусть решение игры , . Обозначим γ₁, γ₂,…, γ_n выигрыши игрока 1 при использовании игроком 2 чистых стратегий y₁, y₂,…, y_n.

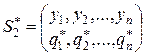
Из определения оптимальной стратегии следует, что любое отклонение игрока 2 от стратегии не может быть ему выгодно, поэтому его проигрыши γ₁ ≥ γ, γ₂ ≥ γ,…, γ_n ≥ γ. Но возможно ли это? Поскольку в стратегии чистые стратегии y₁, y₂,…, y_n применяются с частотами q₁, q₂,…, q_n, то средний проигрыш игрока B (цена игры)

(4.2.3)

Очевидно, что если хотя бы одна из величин γ₁, γ₂,…, γ_n больше γ, то есть равна γ+∆γ, а другие равны γ, то это противоречит системе (4.2.3). Таким образом, доказано свойство оптимальных смешанных стратегий.

Итак, все сказанное справедливо, если игровая ситуация повторяется многократно в сходных условиях и осреднение результатов игр допустимо; каждый игрок не имеет информации о конкретном, хотя и случайном выборе стратегии другим игроком. Если же игрок 2 информирован о действиях игрока 1, то есть знает его конкретную стратегию x_i в каждом повторении игры, то средний выигрыш игрока 1 при использовании им смешанной стратегии может оказаться меньше гарантированной при максиминной чистой стратегии нижней цены игры α. В этом случае игрок 2 наказывает игрока 1 за отклонение от максиминной чистой стратегии.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Основная теорема матричных игр (Дж.фон Неймана) утверждает, что каждая окончательная матричная

Основная аксиома матричных игр (Дж.фон Неймана) утверждает, что любая конечная матричная забава имеет решение в _ стратегиях
(*ответ*) смешанных
Отклики величаются переменными Бернулли, если они
(*ответ*) принимают лишь два значения
nbsp;принимают значения из промежутка (0,1)
nbsp;имеют рассредотачиванием Пуассона
nbsp;имеют обычное рассредотачивание
nbsp;линейны
Отличие последовательности псевдослучайных чисел от последовательности подлинно случайных чисел содержится в том, что первая является _
(*ответ*) повторяющейся
Условная пропускная способность есть
(*ответ*) отношение среднего числа заявок, обслуживаемых системой в единицу медли, к среднему числу поступающих за это время заявок
nbsp;номинальная производительность системы
nbsp;среднее число заявок, которое может обслужить система в единицу времени
nbsp;математическое ожидание интенсивности обслуживания
nbsp;наибольшая производительность системы
Ошибка второго рода статистического аспекта совпадения режимов есть
(*ответ*) возможность принять догадку о совпадении режимов в ситуации, когда они различны
nbsp;превышение заданного уровня расхождения меж значениями
nbsp;неправильный выбор критерия
nbsp;подбор ошибочного закона рассредотачивания
nbsp;вероятность отвергнуть гипотезу о совпадении режимов в ситуации, когда они совпадают
Ошибка первого рода статистического критерия совпадения режимов есть
(*ответ*) возможность отторгнуть гипотезу о совпадении режимов в ситуации, когда они совпадают
nbsp;вероятность принять гипотезу о совпадении режимов в ситуации, когда они разны
nbsp;неправильный выбор аспекта
nbsp;подбор ошибочного закона рассредотачивания
nbsp;превышение данного уровня расхождения между значениями
Пассивными блоками модели являются блоки _ транзактов
(*ответ*) хранения
nbsp;генерации
nbsp;обработки
nbsp;хранения и генерации
nbsp;генерации и перемещения
Полное документирование метода моделирования, моделирующей программки и каждого модуля безусловно нужно для того, чтоб
(*ответ*) избежать дорогостоящих ошибок и упростить разработку программки
nbsp;можно было уверить заказчика в корректности работы модели
nbsp;удовлетворить требованиям эталонов на программное обеспечение
nbsp;облегчить проверку структуры модели
nbsp;облегчить составление отчета
Полным факторным тестом называется эксперимент, в котором
(*ответ*) реализуются все вероятные композиции уровней самостоятельных переменных
nbsp;учтены все уровни всех причин
nbsp;два уровня данного фактора комбинируются со всеми уровнями всех иных факторов
nbsp;учтены все уровни данного фактора
nbsp;все уровни данного фактора комбинируются с 2-мя уровнями всех иных причин
Последовательность подборки частей из очереди без приоритетов
(*ответ*) подходит правилу чем ранее пришел тем ранее вышел
nbsp;подходит правилу чем позже пришел тем ранее вышел
nbsp;не зависит от медли поступления элемента в очередь
nbsp;на сто процентов определяется значением данного параметра элемента
Последовательность подборки элементов из стека
(*ответ*) подходит правилу чем позднее пришел тем ранее вышел
nbsp;подходит правилу чем ранее пришел тем раньше вышел
nbsp;не зависит от медли поступления элемента в очередь
nbsp;вполне определяется значением заданного параметра элемента

Источник

Понятие стратегии, оптимальной во множестве смешанных стратегий. Основная теорема матричных игр Дж. Фон Неймана

Если нижняя и верхняя цены игры в смешанных стратегиях совпадают, то их общее значение V= =v называется ценой игры в смешанных стратегиях, а стратегии и , для которых выполняется равенство называются оптимальными смешанными стратегиями соответственно игроков А и В. Оптимальные смешанные стратегии и обладают тем свойством, что если один из игроков придерживается своей оптимальной стратегии, то противнику невыгодно отклоняться от своей оптимальной стратегии. Обозначим через множества оптимальных стратегий игроков А и В. Очевидно, что множество оптимальных стратегий каждого из игроков является подмножеством множества смешанных стратегий:

, то есть цена игры в смешанных стратегиях не меньше нижней цены игры в чистых стратегиях α и не больше верхней цены игры в чистых стратегиях β.

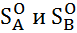
Полным решением игры в смешанных стратегиях называется совокупность множеств оптимальных стратегий игроков и цены игры. Любая пара оптимальных стратегий и и цена игры образуют частное решение в смешанных стратегиях.

Основная теорема матричных игр фон Неймана. Любая матричная игра имеет решение в смешанных стратегиях, то есть существует цена игры в смешанных стратегиях и оптимальные смешанные стратегии и игроков А и В соответственно.

v =

Критерий оптимальности смешанной стратегии игрока А в терминах, задаваемых цены игры в смешанных стратегиях, выигрыш-функции и множества смешанных стратегий игрока В

Теорема (Критерий оптимальных стратегий.)

Пусть V-цена игры, Н(Р,Q) – выигрыш-функция, S_B– множества смешанных стратегий игрока В.

Док-во:

Рассматривая как пок-ль эф-ти стратегии Р 0 относит множ-ва S_B смеш стр-гий игрока В, будем иметь по опр-нию: (3)

Из равенств (2)-(3)получаем (1)

Достаточность. Пусть для некоторой стр-гииР 0 игрока А выполнется нер-во (1)

Для док-ва оптимальности стратегии Р 0 достаточно показать справедливость равенства: (4)

Т.к. нер-во(1) выполняется для любой стратегии Q S_B игрока В, то (5)

Но цена игры V равна нижней цене игры , по опр кот. (6)

Совокуп (5) и (6) эквивалентна рав-ву (4).

Достаточность доказана. Теорема доказана.

Критерий оптимальности смешанной стратегии игрока В в терминах задаваемых цены игры в смешанных стратегиях, выигрыш-функции и множества смешанных стратегий игрока А

Теорема (Критерий оптимальных стратегий.)

Пусть V-цена игры, Н(Р,Q) – выигрыш-функция, S_A – множества смешанных стратегий игрока А.

Для того чтобы стратегияQ 0 игрока В была оптимальной, необходимо и достаточно, чтобы выполнялось неравенство

т.е. выбор игроком В оптимальной стратегии Q 0 гарантирует ему проигрыш Н(Р, Q 0 ), не больший цены игры V, при любой стратегии Р игрока А.

Док-во:

Рассматривая как пок-ль эф-ти стратегии Q 0 относит множ-ва S_A смеш стр-гий игрока A, будем иметь по опр-нию: (3)

Из равенств (2)-(3)получаем (1)

Достаточность. Пусть для некоторой стр-гииQ 0 игрока B выполнется нер-во (1)

Для док-ва оптимальности стратегии Q 0 достаточно показать справедливость равенства: (4)

Т.к. нер-во(1) выполняется для любой стр-гии Q S_B иг-ка В, то (5)

Но цена игры V равна верхней цене игры , по опр кот. (6)

Совокуп (5) и (6) эквивалентна рав-ву (4).

Достаточность доказана. Теорема доказана.

Критерий оптимальности смешанной стратегии игрока А в терминах, задаваемых цены игры в смешанных стратегиях, выигрыш-функции и множества чистых стратегий игрока В

Теорема

Пусть V-цена игры, Н(Р,Q) – выигрыш-функция, = – множества чистых стратегий игрока В.

Док-во:

Пусть справедливо нер-во (2). Т.к. это нер-во имеет место для любой стр-гии Q S_B игрока В, то оно, в частности, будет справедливым и для его чистых стратегий В_j , j=1,…,n, т.е. нер-во (1) имеет место =>
импиликация (2)=>(1) доказана.

Теперь пусть имеет место быть нер-во (1). Тогда по ф-ле с учетом того, что 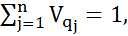получим

Q S_{B ,} т.е. доказано нер-во (2). Т.о., справедлива импликация(1)=>(2) => эквивалентны

Источник

09. Основные теоремы матричных игр

,

Которая может рассматриваться в качестве характеристики выбранных SА и SB.

Формируя свою стратегию SА в антагонистической игре, игрок А в соответствии с принципом максимина должен выбрать такую стратегию, при которой минимально возможный выигрыш был бы максимален, т. е. такую стратегию, которая обеспечивает

(2.7)

Аналогичные рассуждения, связанные с поиском оптимальной смешанной стратегии игрока В, приводят к рекомендации выбрать такую стратегию SB, которая обеспечивает

. (2.8)

Весьма важным для теории и практики является вопрос о том, связаны ли между собой VА и VB. Ответ на него дает теорема о максимине.

Теорема о максимине. В конечной игре двух игроков (коалиций) с нулевой суммой (матричной игре) при Имеет место равенство

. (2.9)

Теорема о максимине указывает на существование равновесия для случая VА=VB, при и, следовательно, существования оптимальных смешанных стратегий.

Поэтому другая формулировка теоремы о максимине, называемая основной теоремой матричных игр определяется следующим образом.

Основная теорема матричных игр. Любая матричная игра имеет, по крайней мере, одно оптимальное решение, в общем случае, в смешанных стратегиях и соответствующую цену V.

Т. е. лежит между нижней a и верхней b ценами игры.

Оптимальное решение игры в смешанных стратегиях, также как и решение в чистых стратегиях, обладает тем свойством, что каждый из игроков не заинтересован в отходе от своей оптимальной смешанной стратегии, если его противник применяет свою оптимальную смешанную стратегию, так как это ему невыгодно.

Определение. Те из чистых стратегий игроков А и В, которые входят в их оптимальные смешанные стратегии с вероятностями, не равными нулю, называются Активными стратегиями.

Существует теорема об активных стратегиях, применение которой позволяет упрощать решение некоторых матричных игр.

Теорема об активных стратегиях. Если один из участников матричной игры G (MXN), придерживается своей оптимальной смешанной стратегии, то это обеспечивает ему максимальный средний выигрыш, равный цене игры n, независимо от того, какие действия предпринимает другой игрок, если только он не выходит за пределы своих активных стратегий (т. е. пользуется любой из них в чистом виде или смешивает их в любых пропорциях), причем число активных стратегий каждого игрока, входящих в их оптимальные смешанные стратегии, не превосходит L, где L = min(m, n).

Использование данной теоремы позволяет в частности, упрощать решение матричных игр 2XN и MX2.

Источник

Основная теорема теории матричных игр – теорема существования решения в смешанных стратегиях Дж. Фон Неймана

Теория игр как наука, изучающая поведение многих участников, когда достигаемые каждым результаты зависят от действий остальных. Основная и формализованная теорема матричных игр фон Неймана, особенности и принципы ее применения в процессе управления.

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

Размещено на http://www.allbest.ru/

1. Теоретическая часть

Итак, основная теорема матричных игр фон Неймана гласит: любая матричная игра имеет решение в смешанных стратегиях, т.е. существуют цена игры в смешанных стратегиях V и оптимальные смешанные стратегии P 0 и Q 0 соответственно игроков A и B.

Формализованная запись теорема будет дана позже. Как мы видим, в теореме присутствуют такие термины как игра, матричная игра, стратегии, смешанные стратегии, цена игры, цена игры в смешанных стратегиях и оптимальные смешанные стратегии. Я считаю, что прежде чем разбирать и доказывать данную теорему, необходимо вкратце дать теоретический материал по приведённым выше терминам.

В то же время каждую смешанную стратегию можно представить линейной комбинацией чистых стратегий с коэффициентами, являющимися координатами данной смешанной стратегии:

управление нейман матричный

Если говорить о смешанных стратегиях, то нижняя цены игры обозначается

Цены в смешанных и чистых стратегиях взаимосвязаны с между собой. Нижняя цена игры иверхняя цена игры в в чистых стратегиях, нижняя цена игры и верхняя цена игры в смешанных стратегиях удовлетворяют следующим неравенствам:

Итак, ознакомившись с базовыми понятиями, перейдём к самой теореме. Для Любая матричная игра имеет решение в смешанных стратегиях, т.е. существуют цена игры в смешанных стратегиях V и оптимальные смешанные стратегии P 0 и Q 0 соответственно игроков A и B, т.е:

Для того, чтобы доказать данную теорему необходимо ввести понятие выпуклой функции и седловых точек функции. Для удобства все формулы будут пронумерованы. Числовая функция называется выпуклой на выпуклом множестве X, если для любых точек и произвольного числа справедливо неравенство

Определение строго выпуклой функции вытекает, если ужесточить определение выпуклой функции, потребовав вместо неравенства (1.2) строгое неравенство для любых точек x`,x« X, x`x« и произвольного

Функция называется вогнутой на выпуклом множестве X, если для любых двух точек справедливо неравенство

Соответственно, функции называется строго вогнутой на выпуклом множестве X если для любых двух точек x`, x«? X и произвольного числа л?[0,1] справедливо неравенство

можно переписать в виде неравенства

которое соответствует неравенству 1.6, а равенство в виде равенства

В общем случае седловые точки произвольных функций двух векторных аргументов также обладают свойствами равнозначности и взаимозаменяемости. Доказательство закончено.

2. Практическая часть

Источник