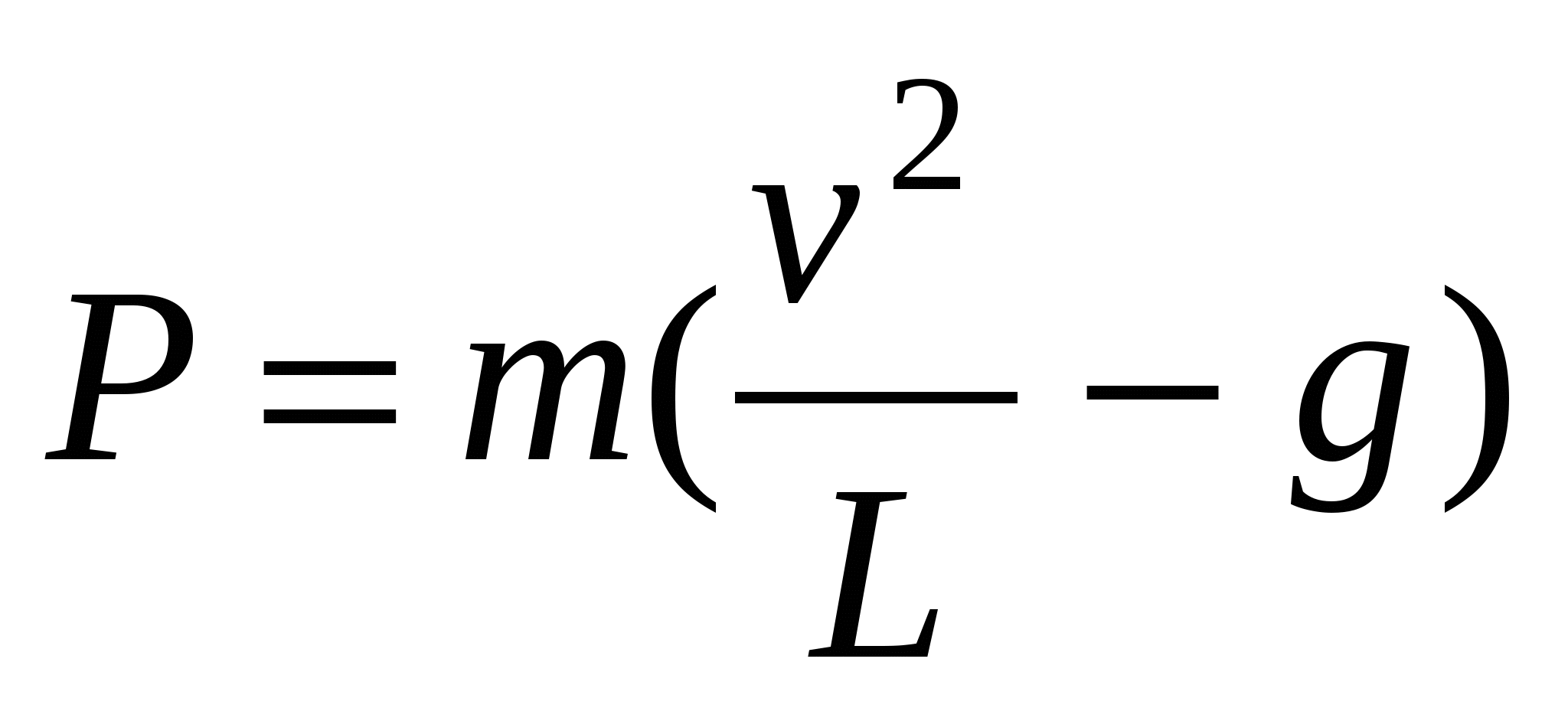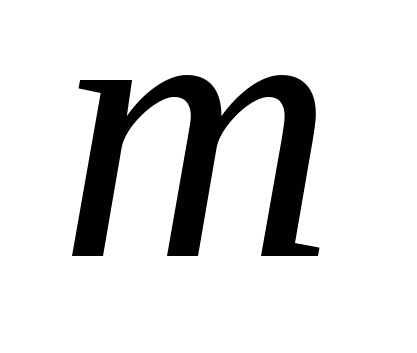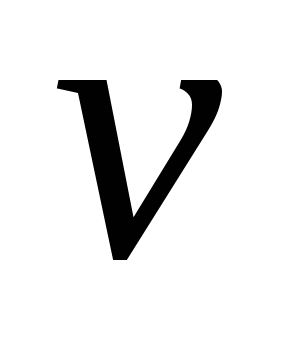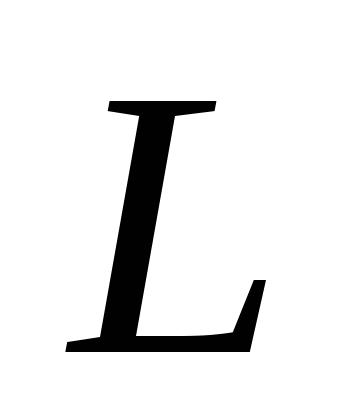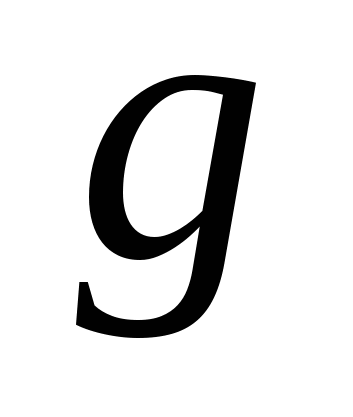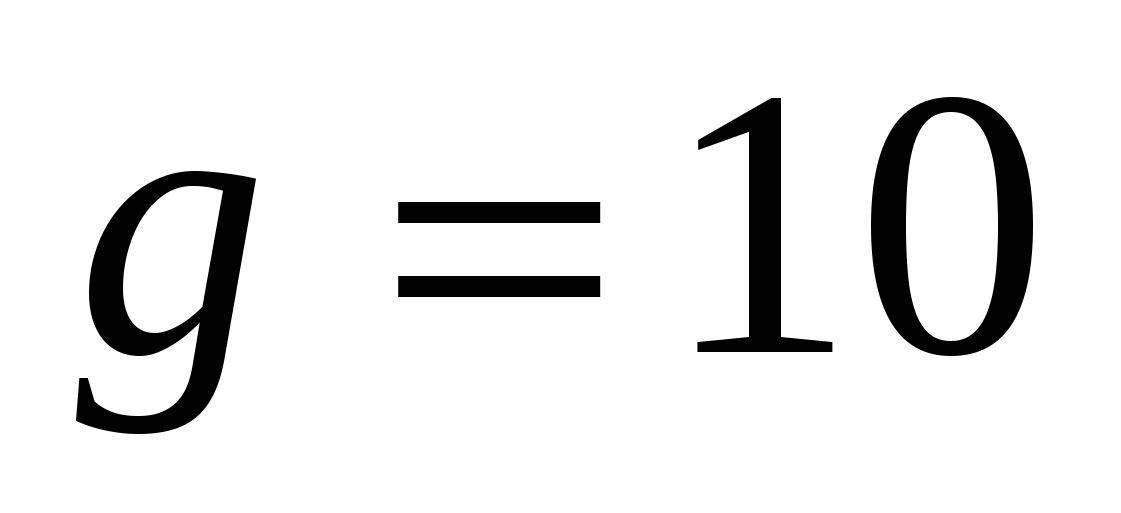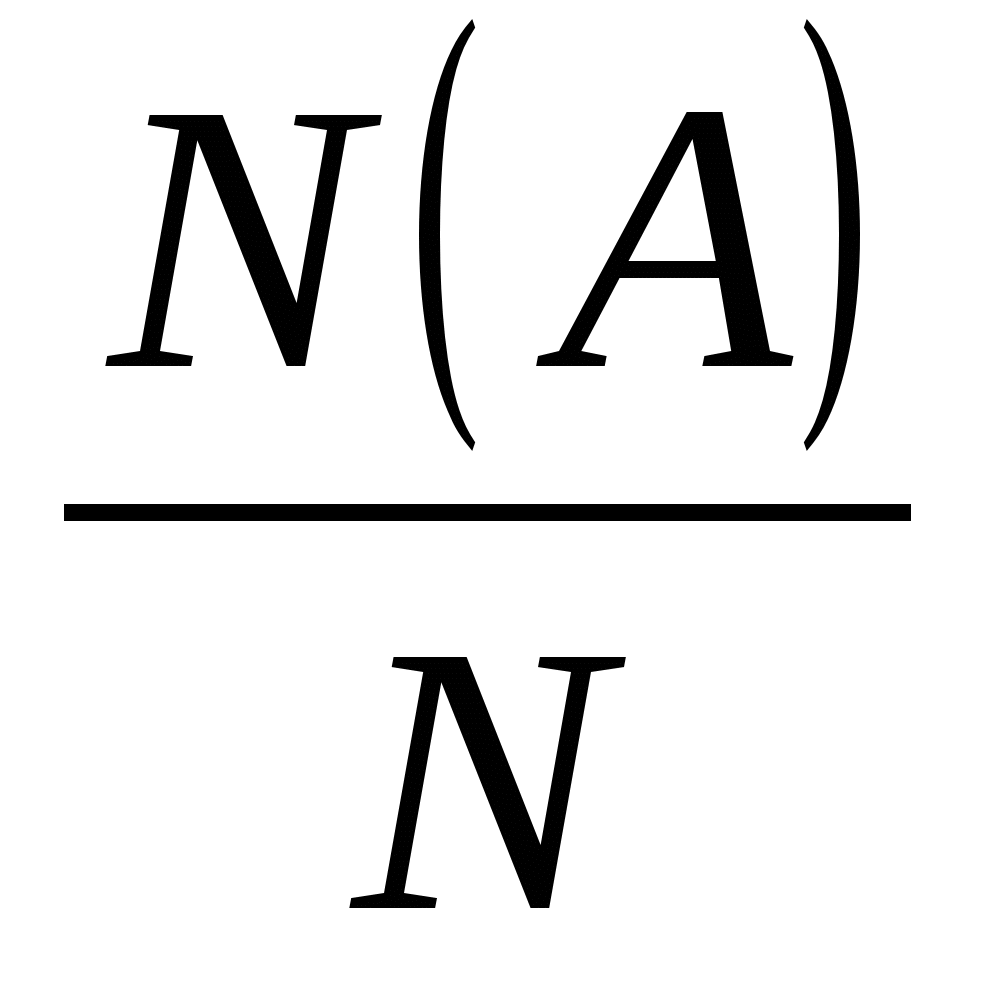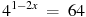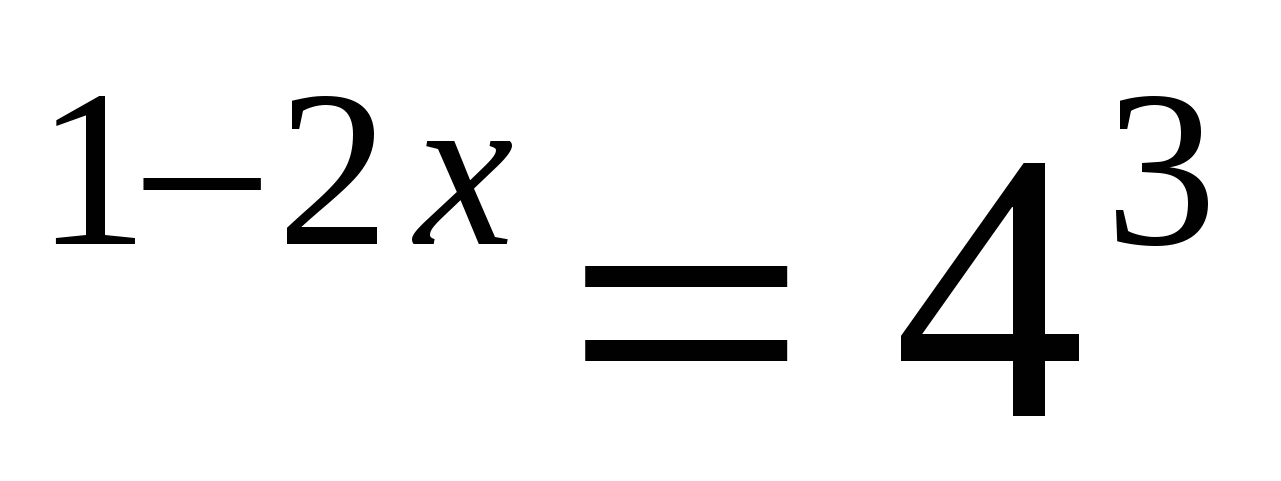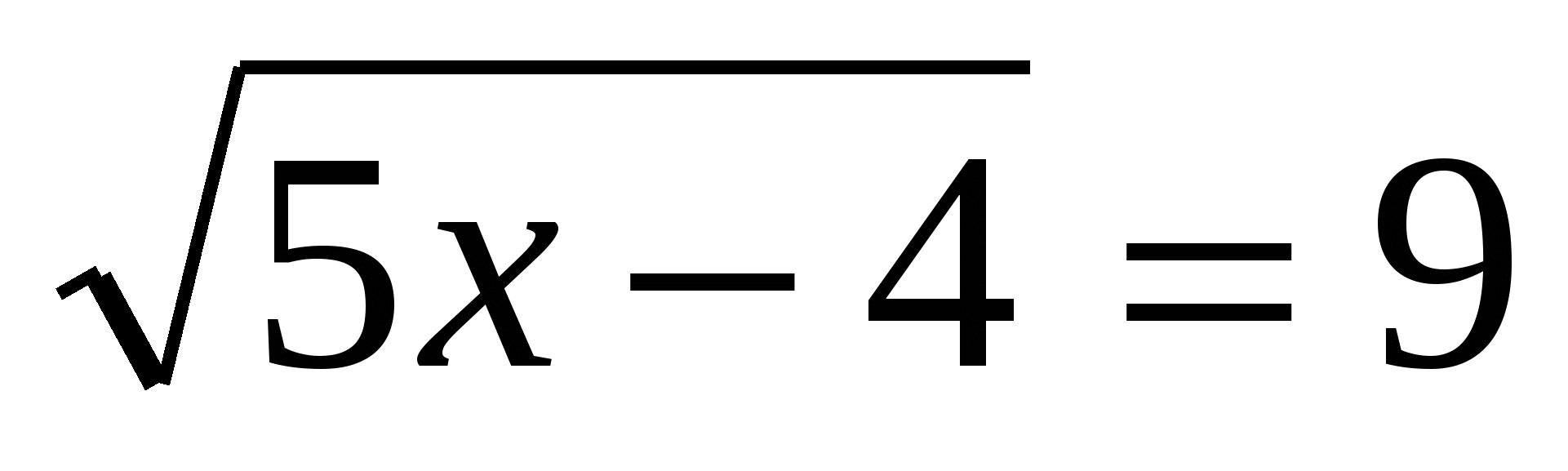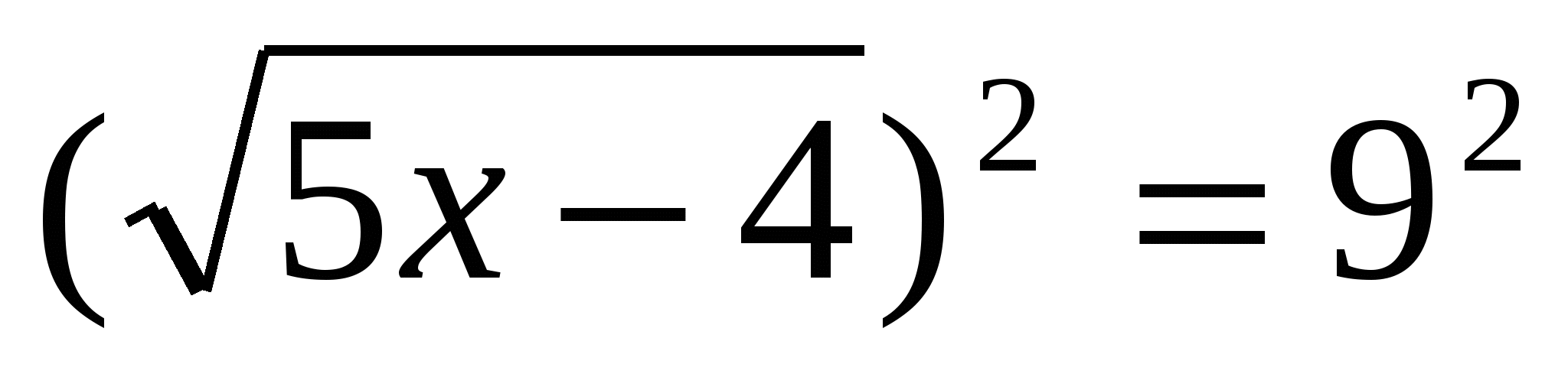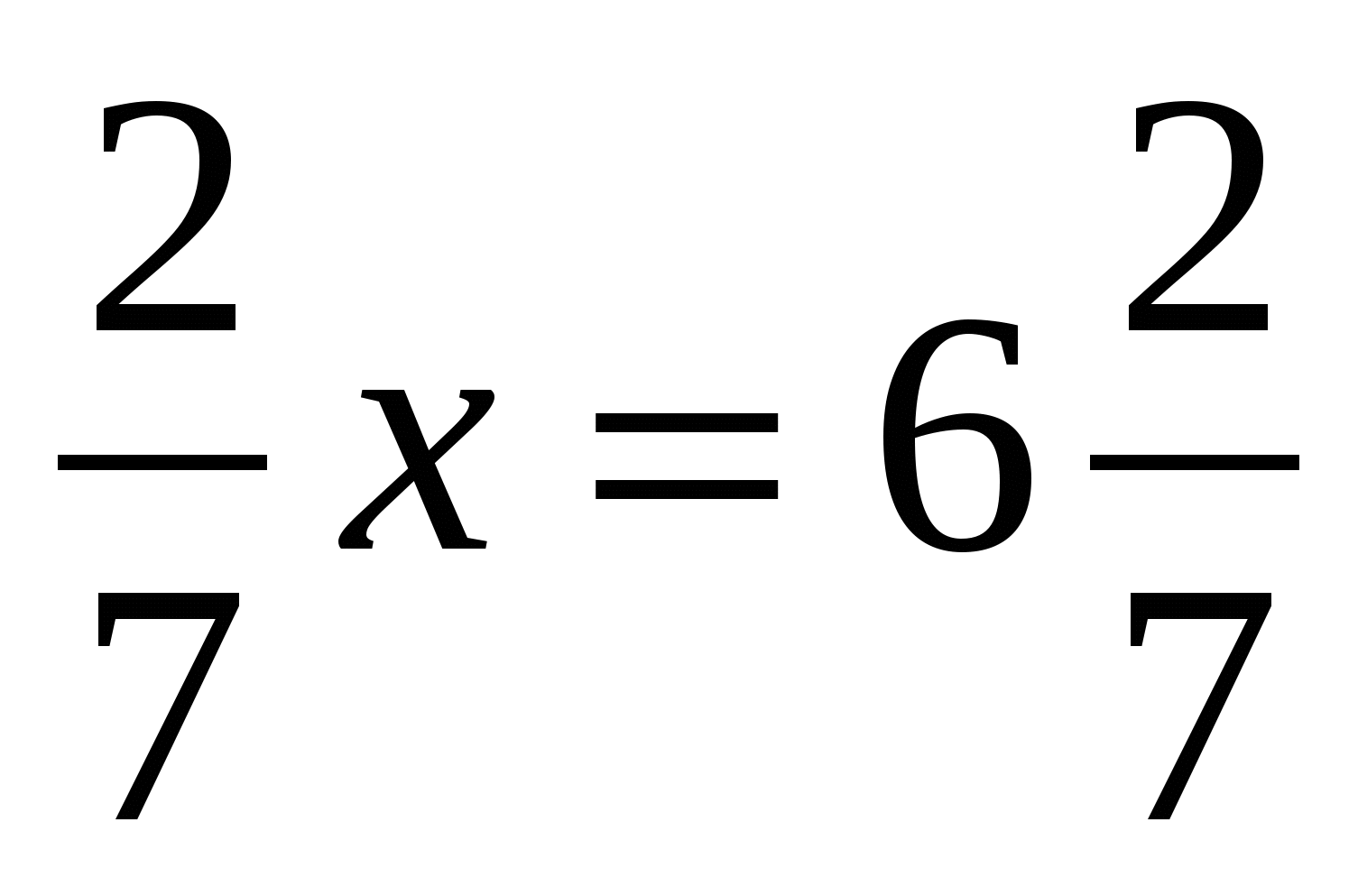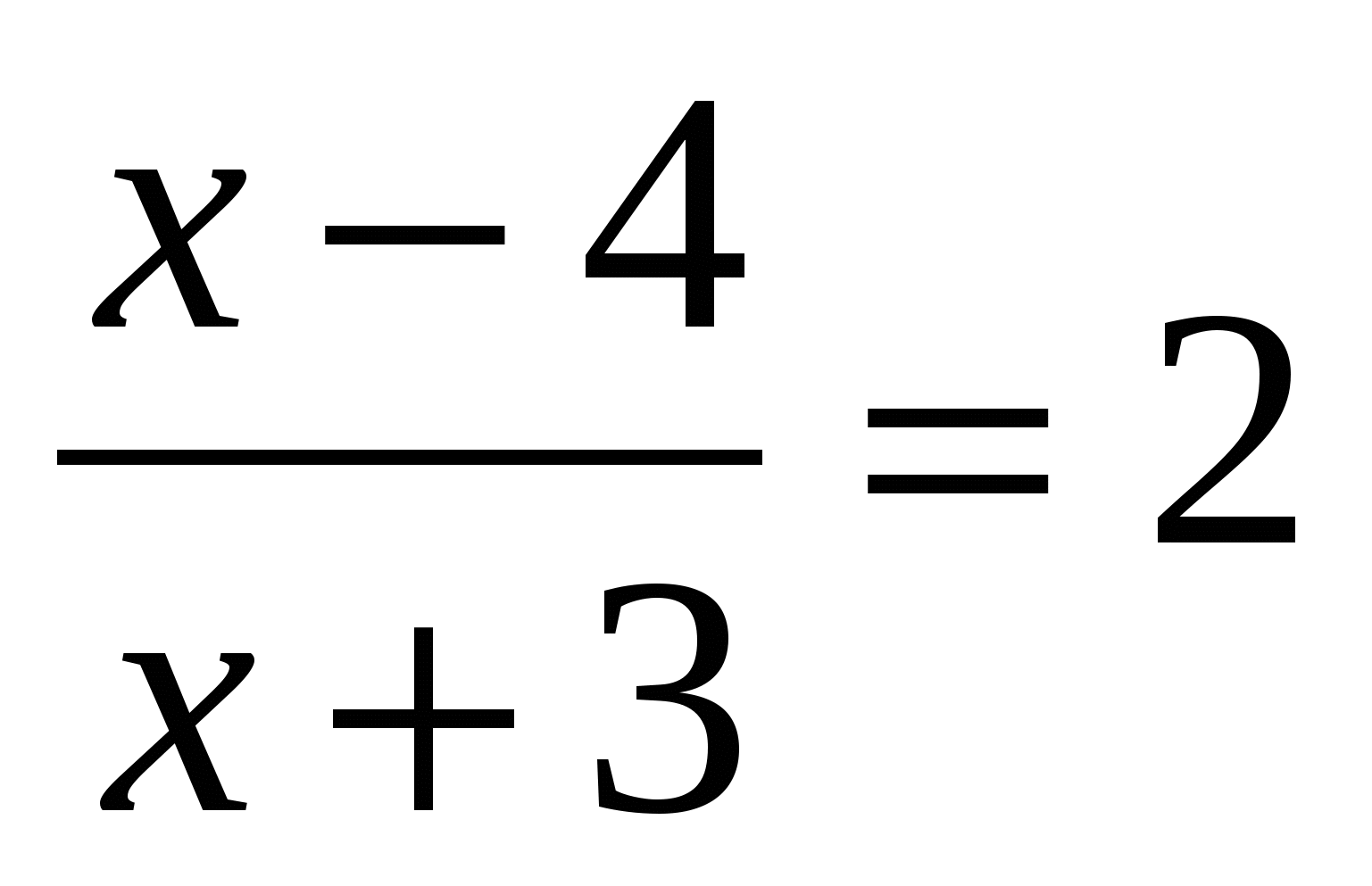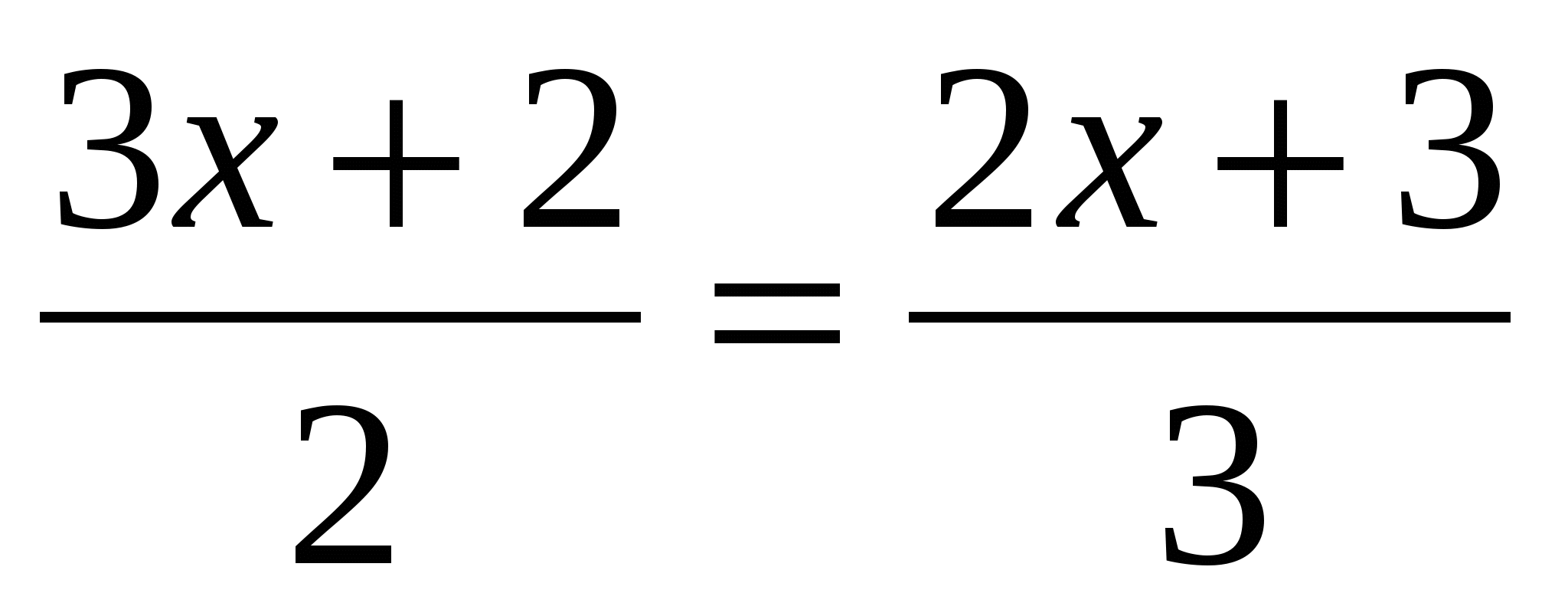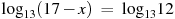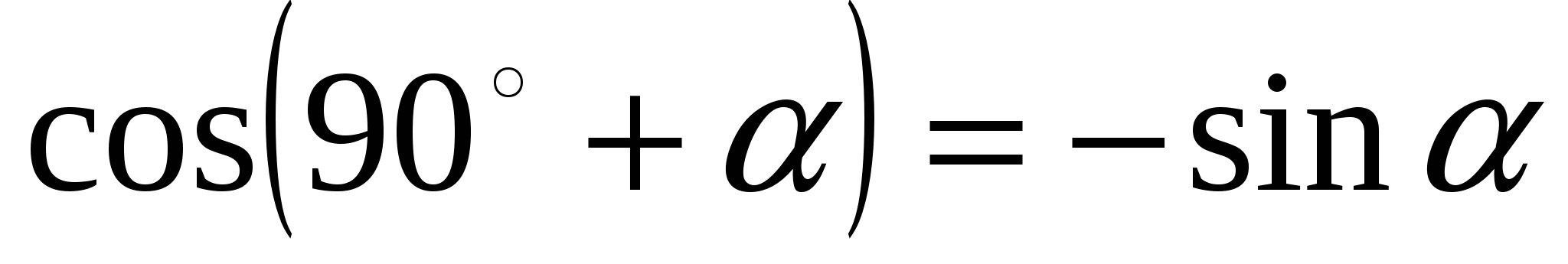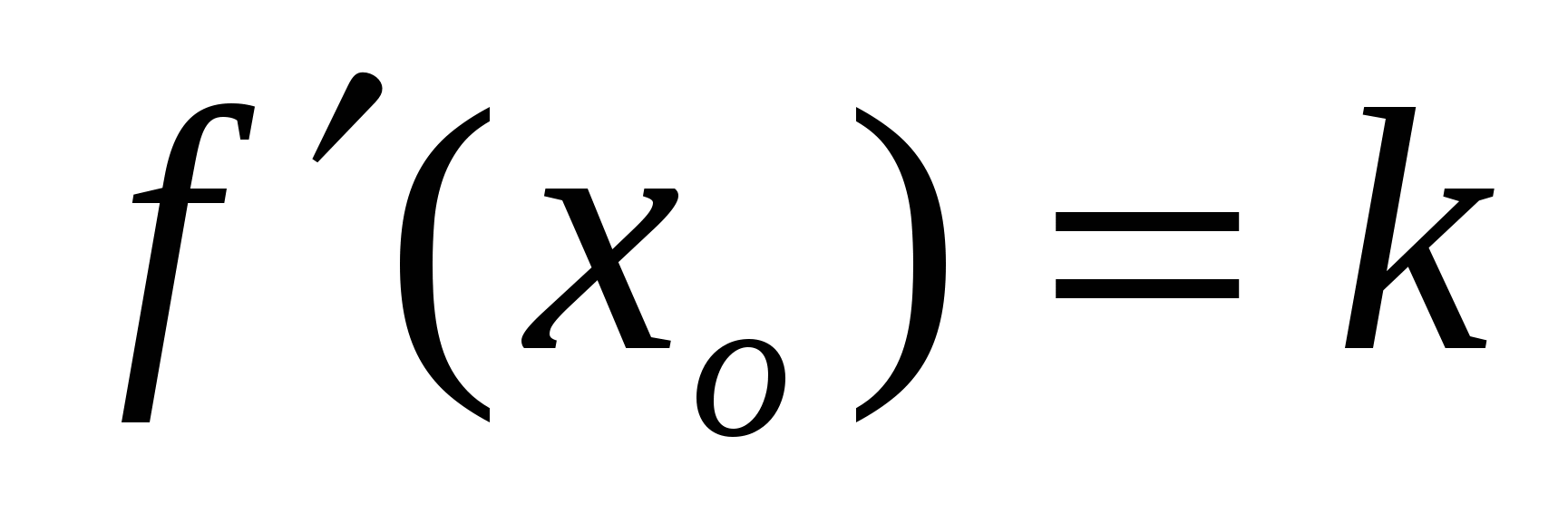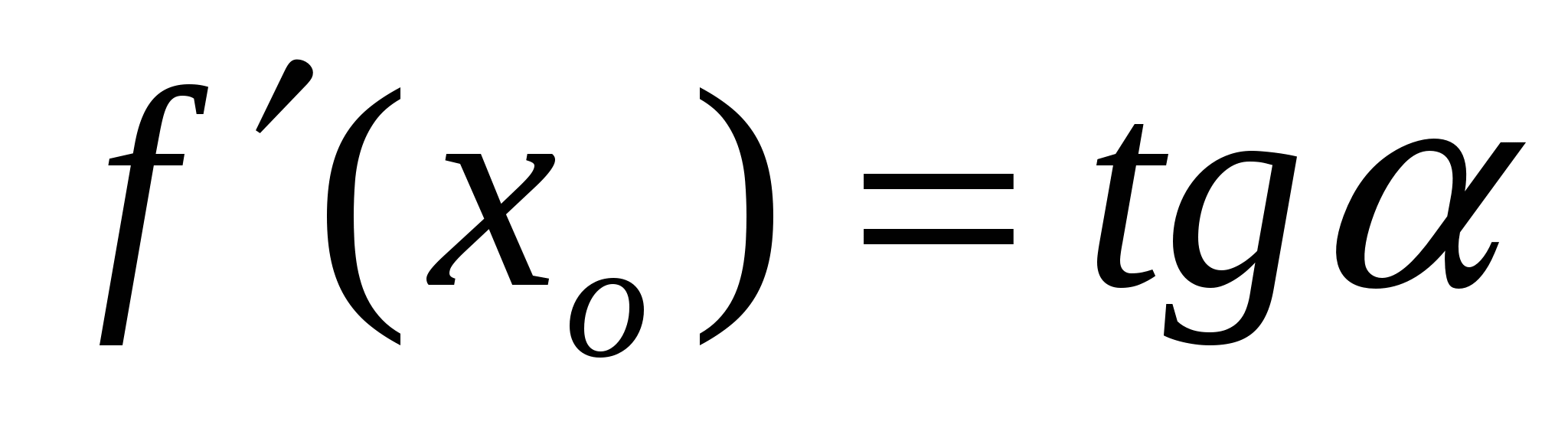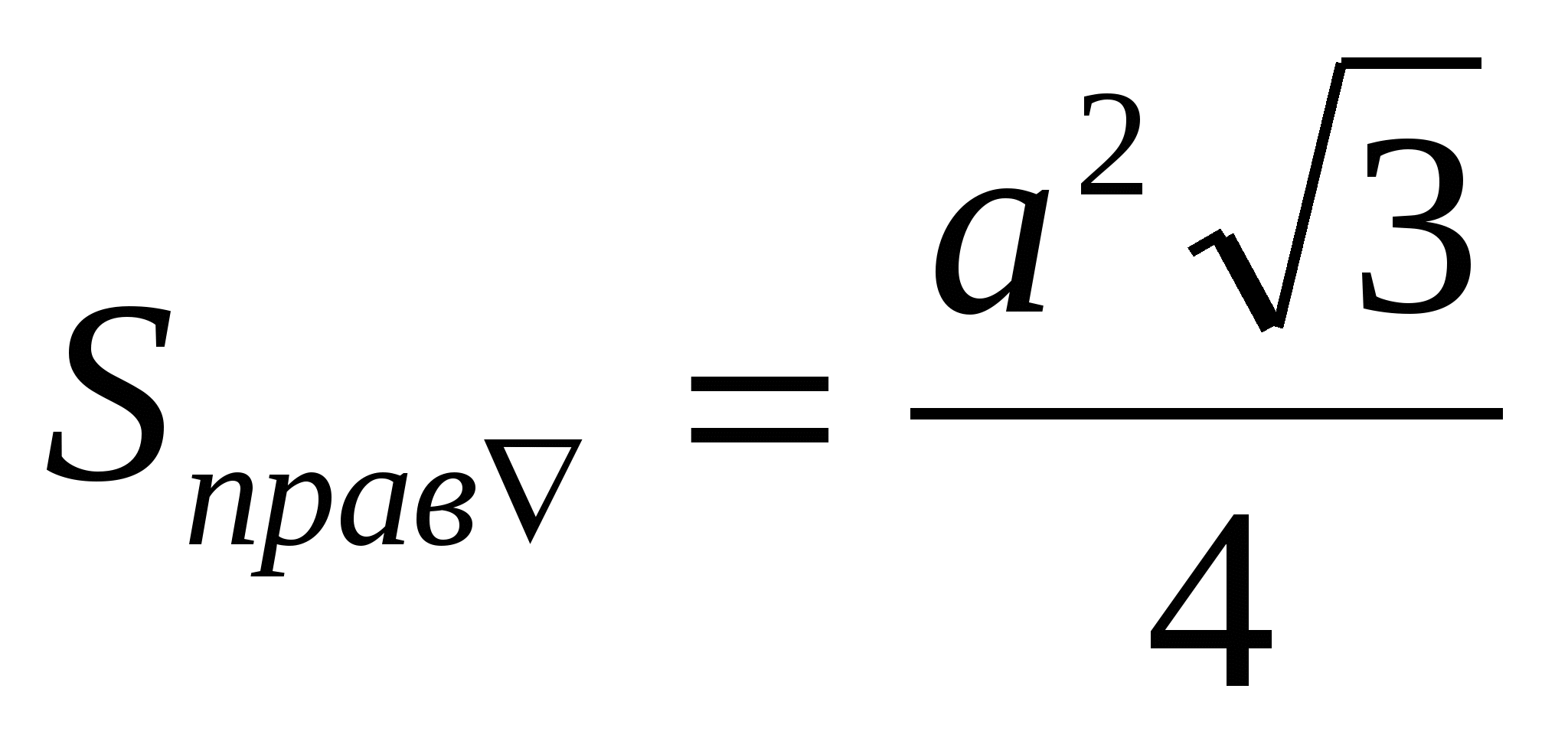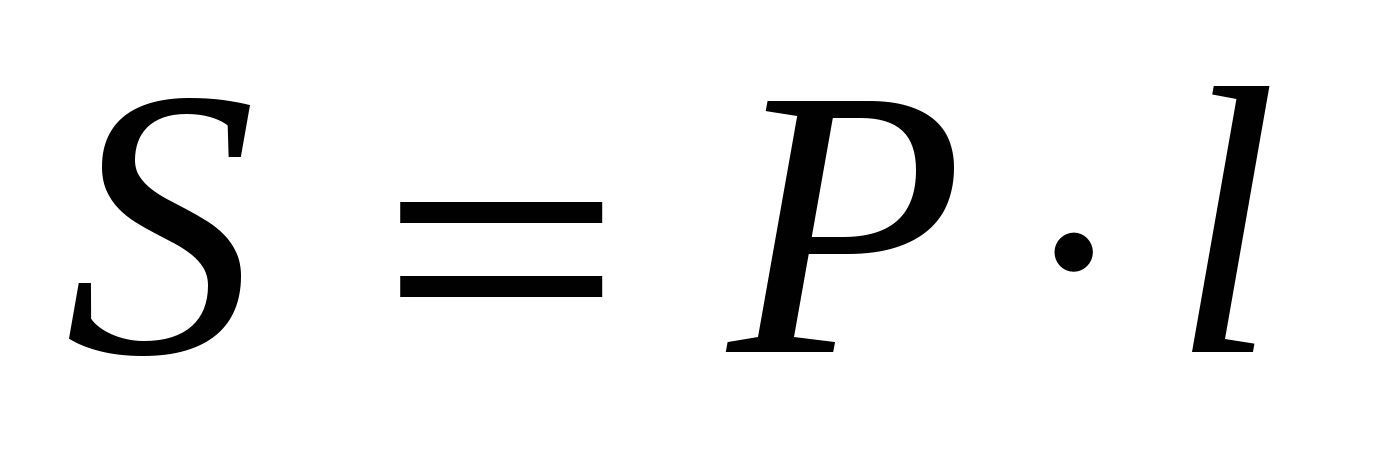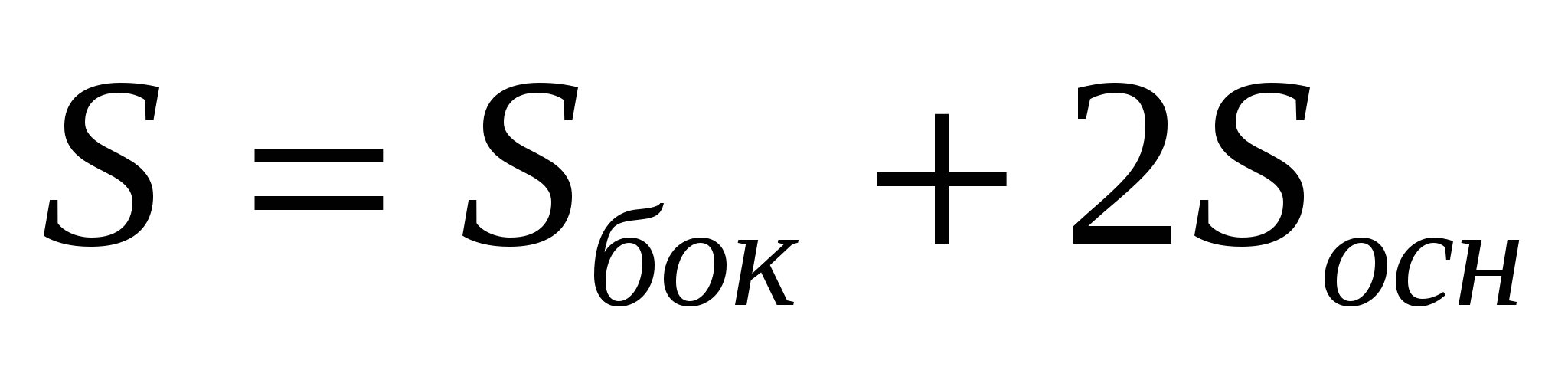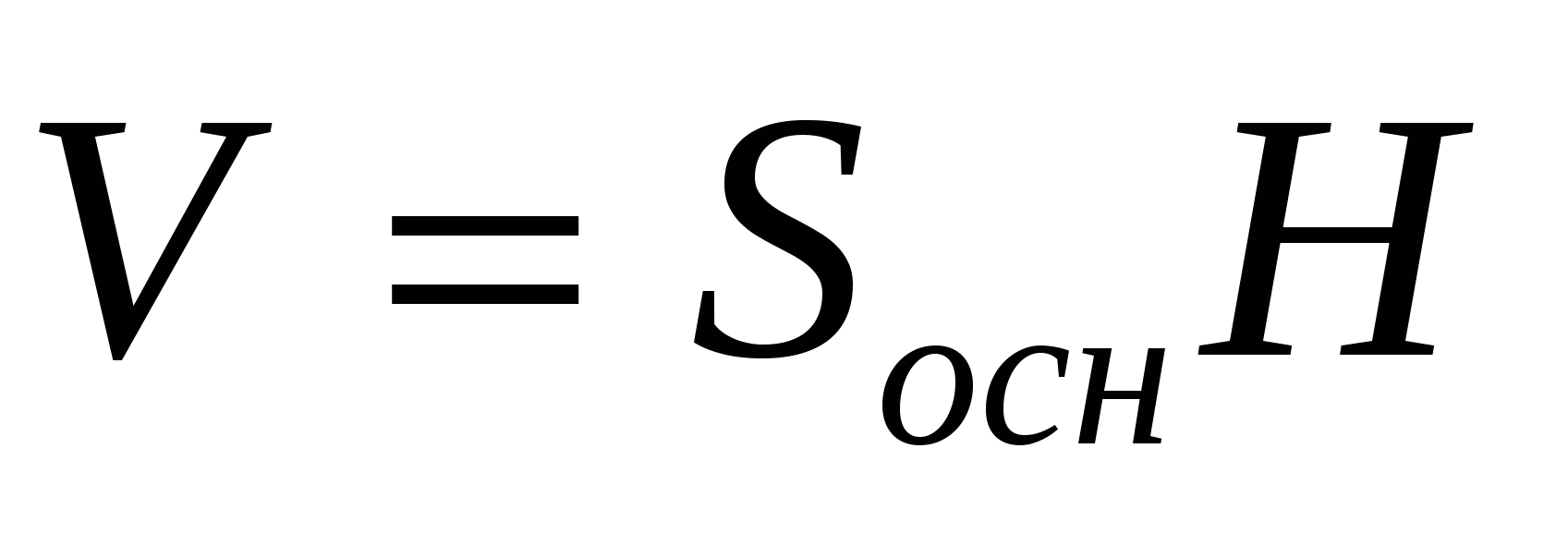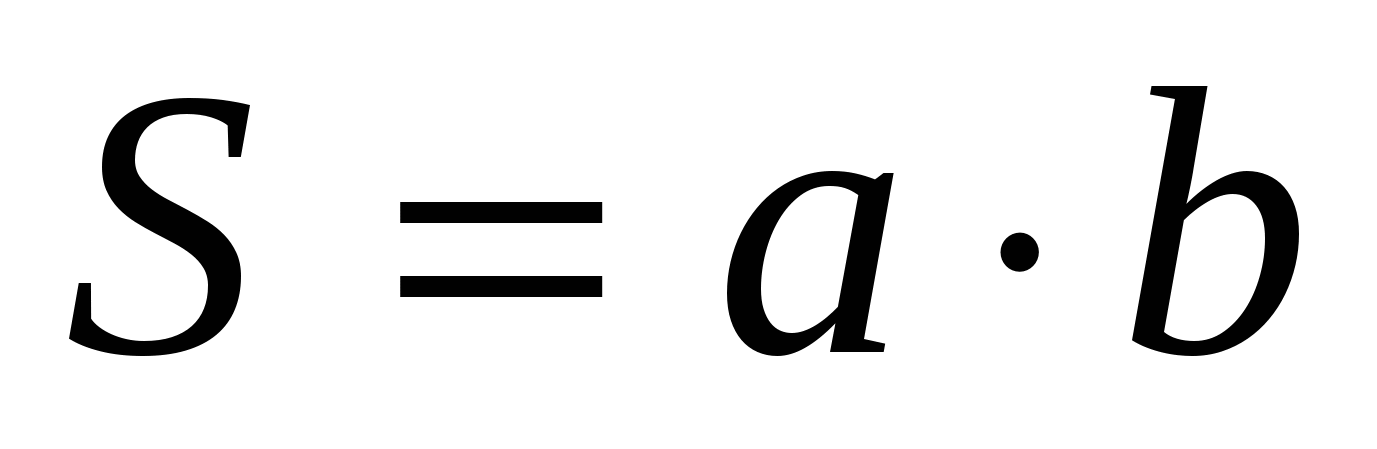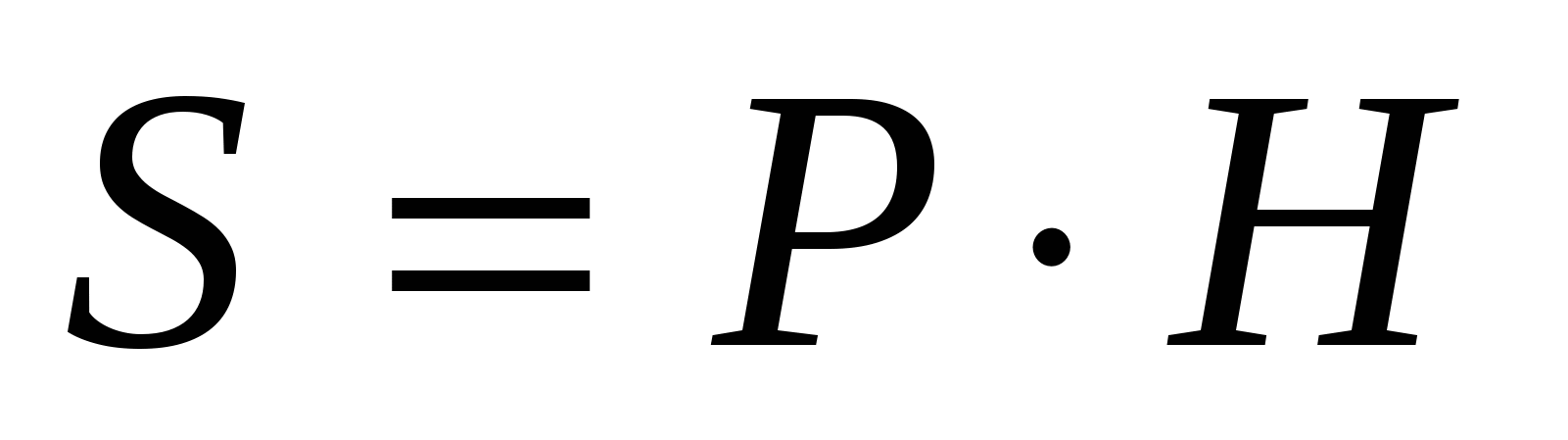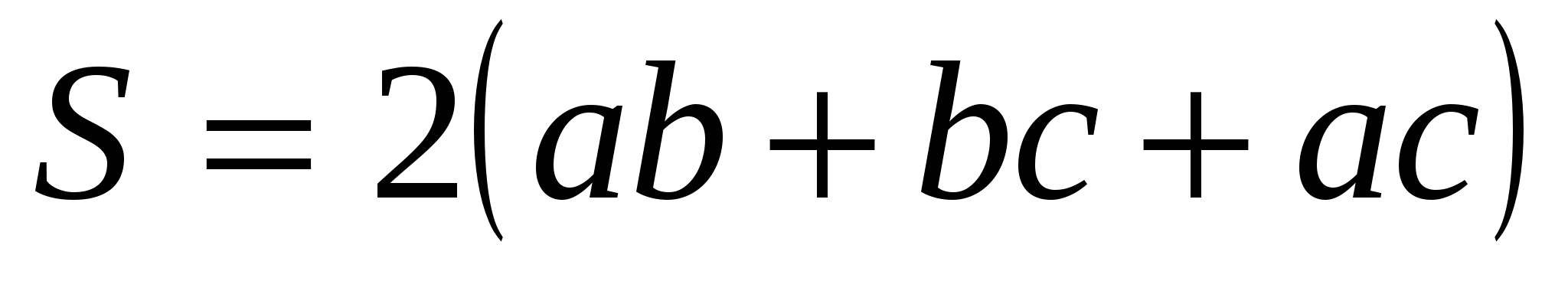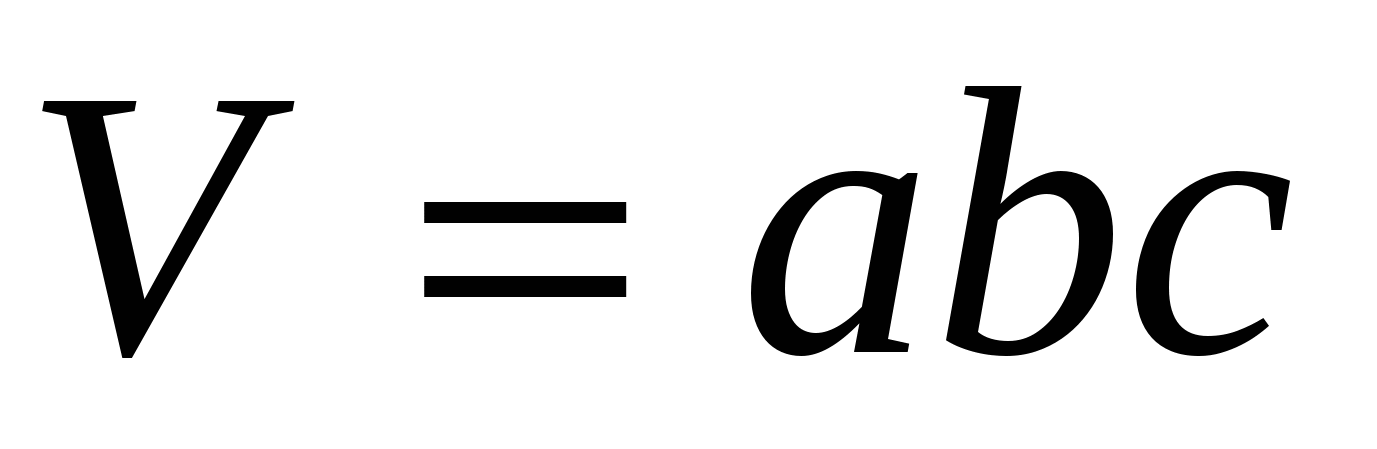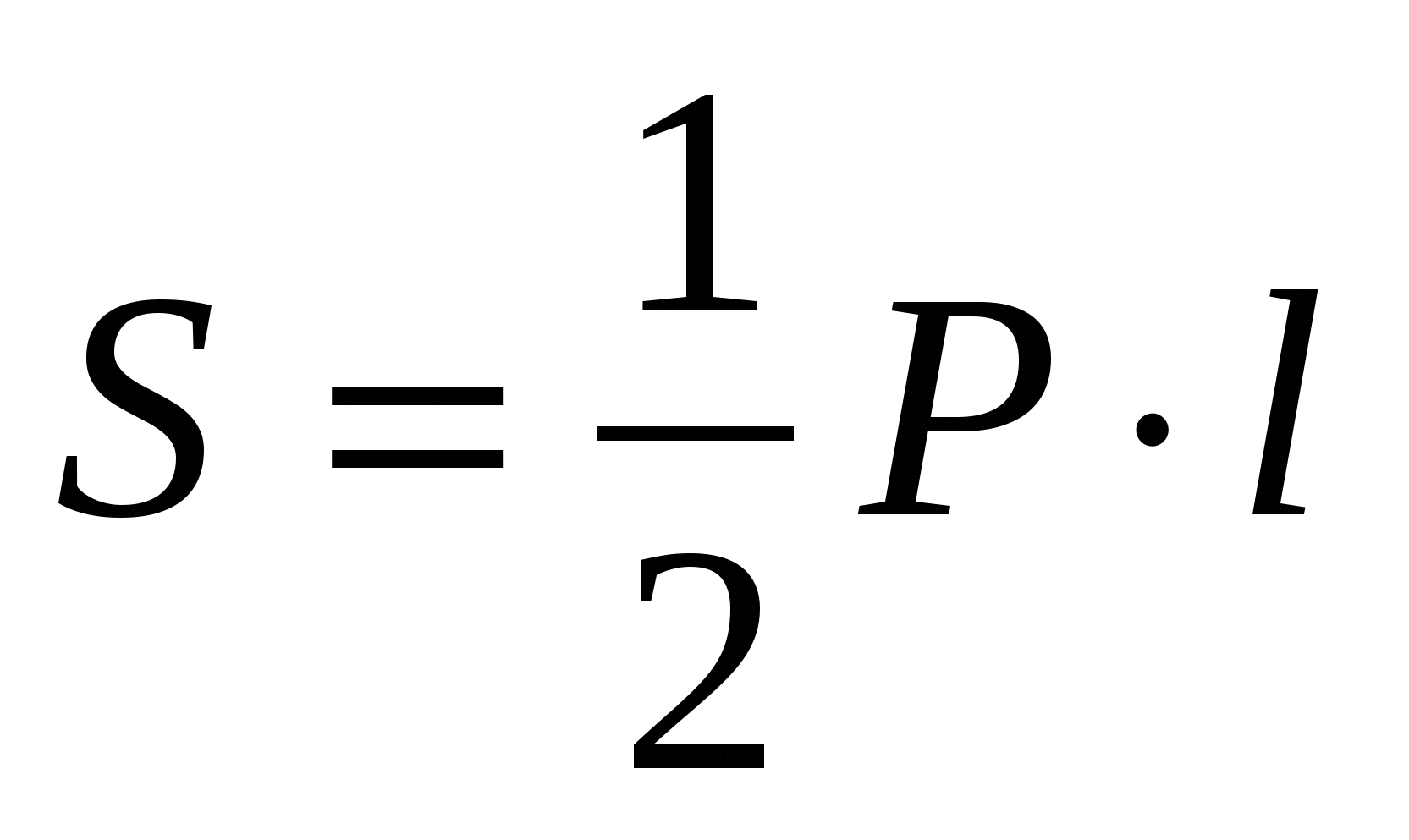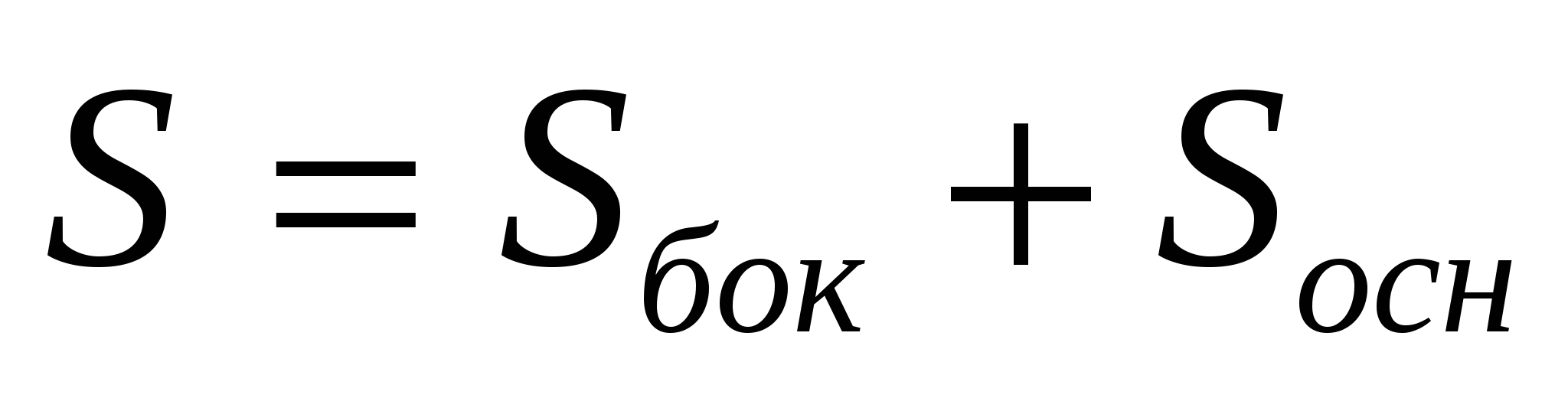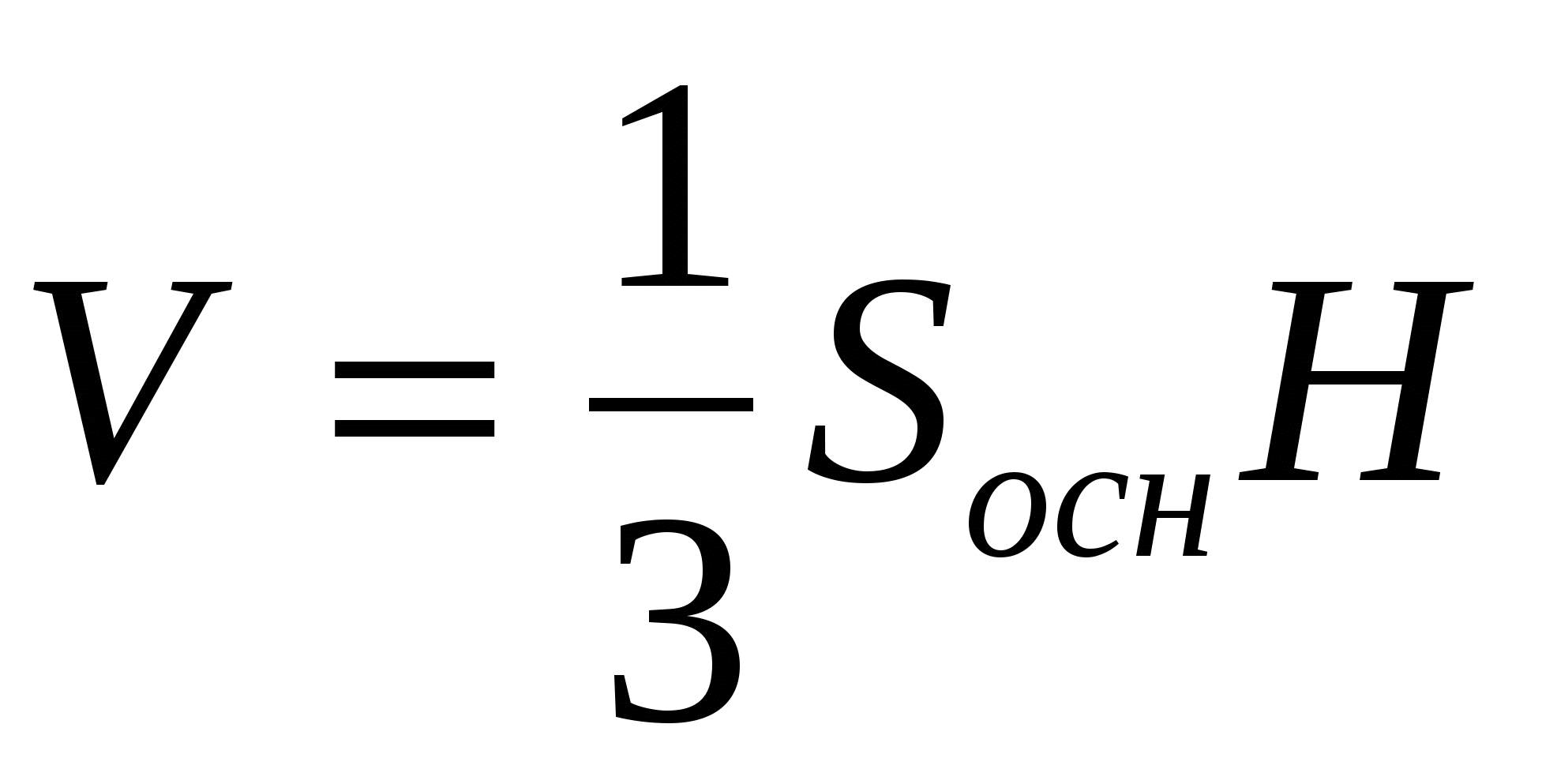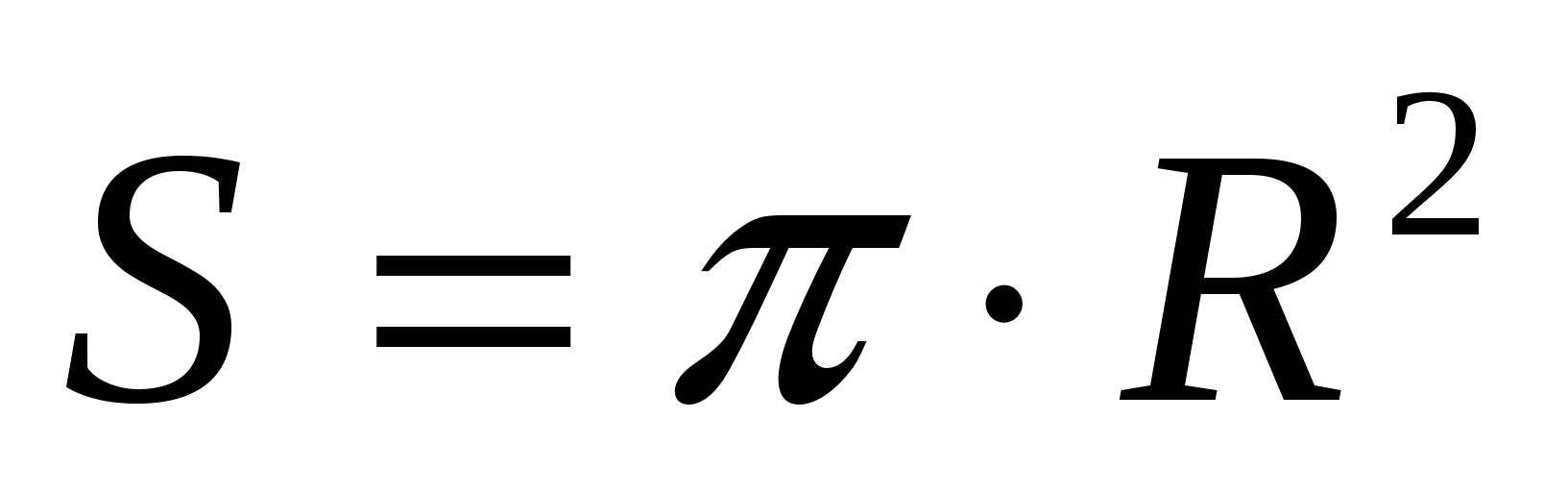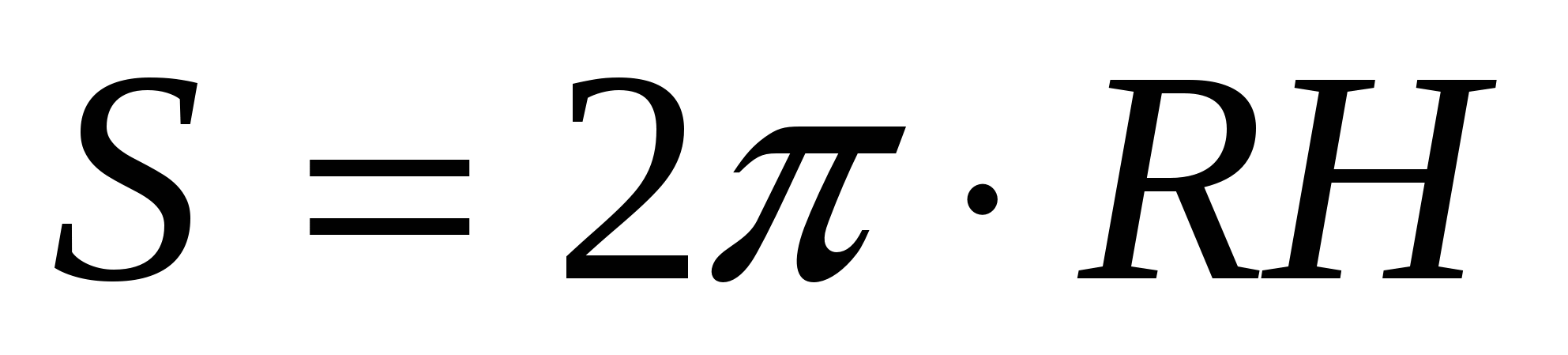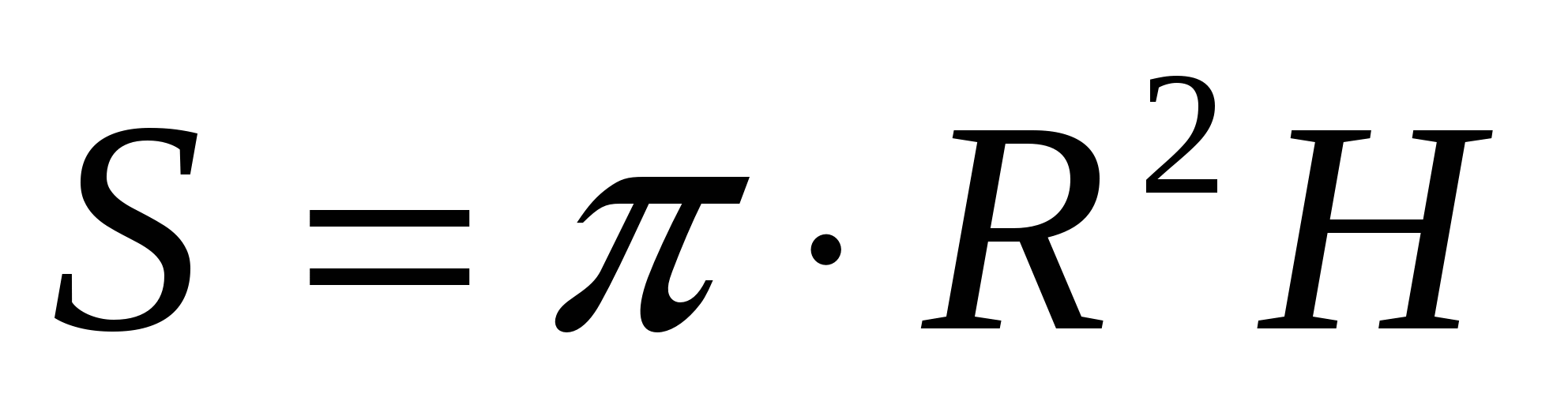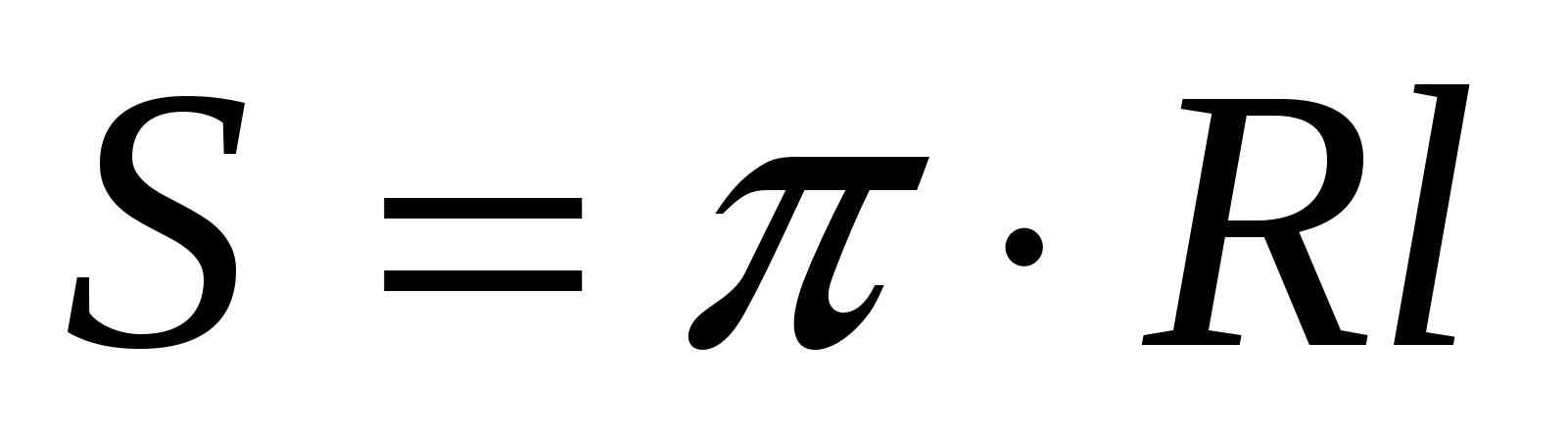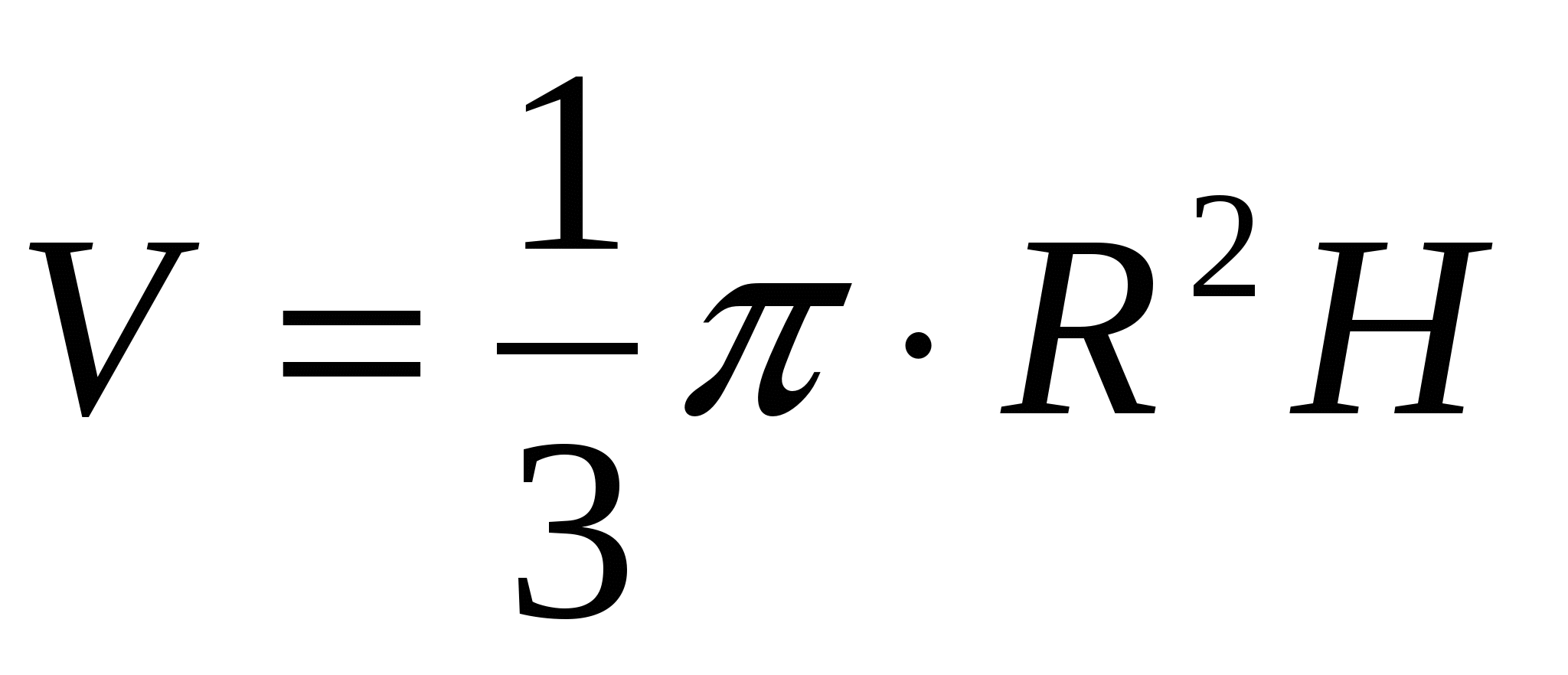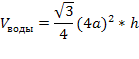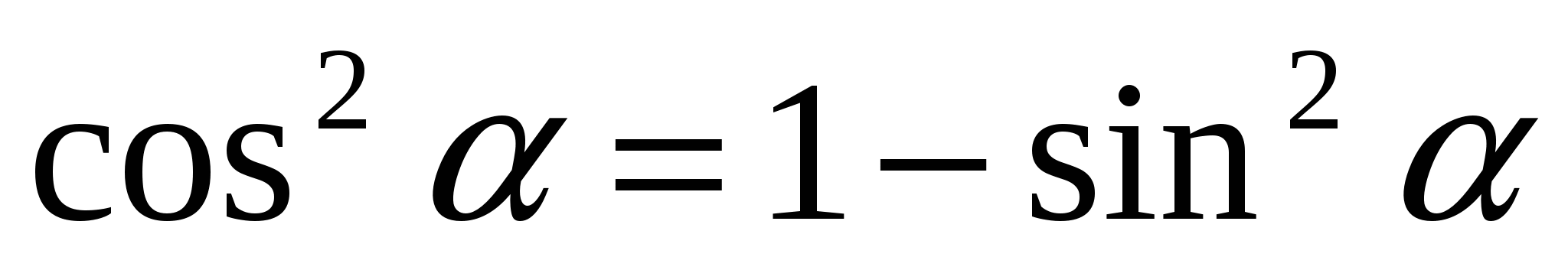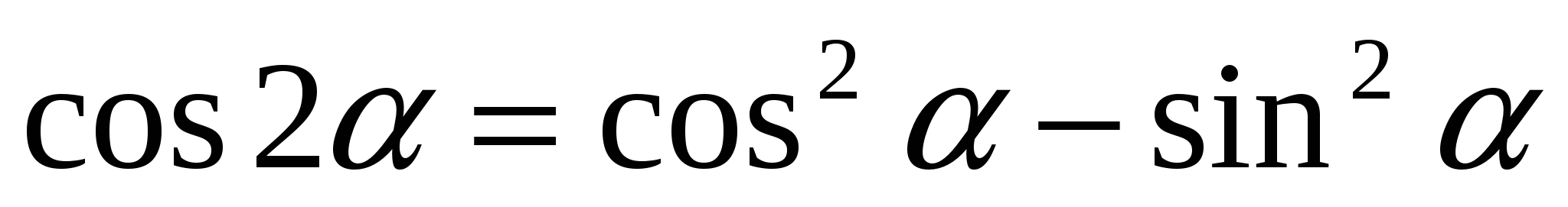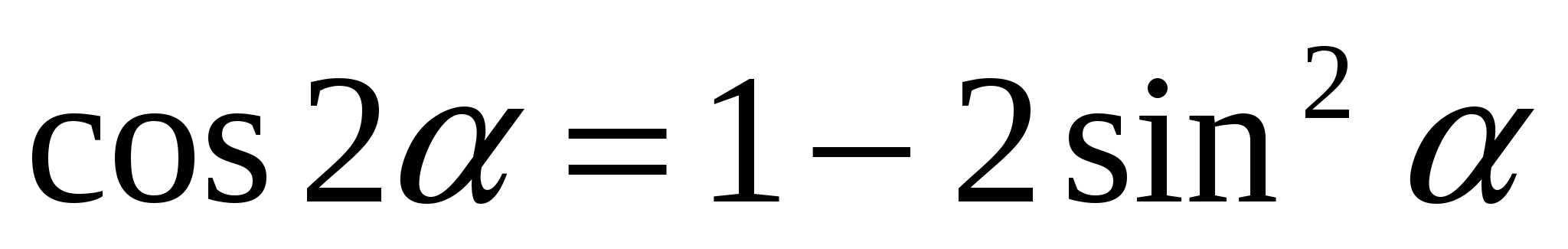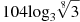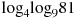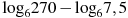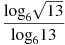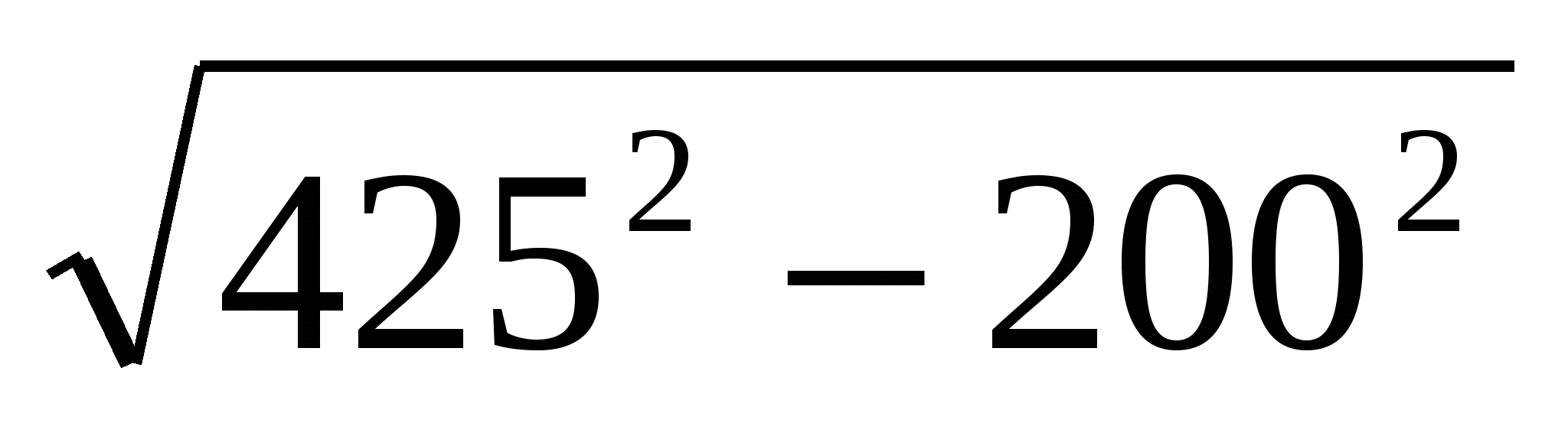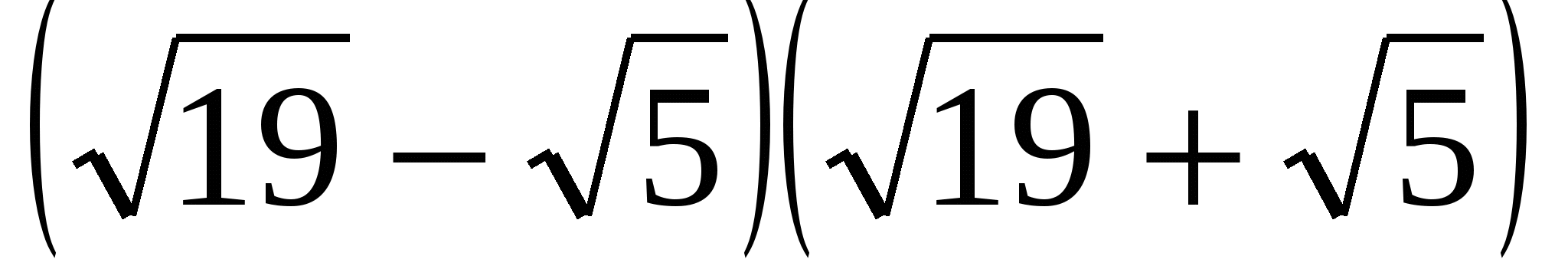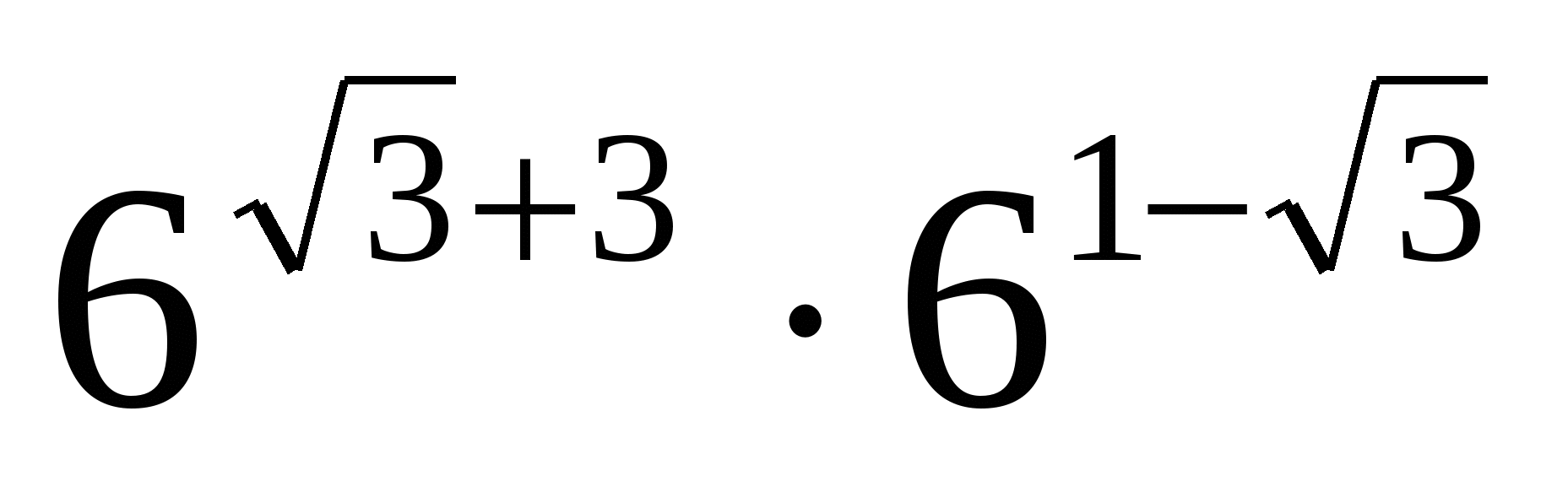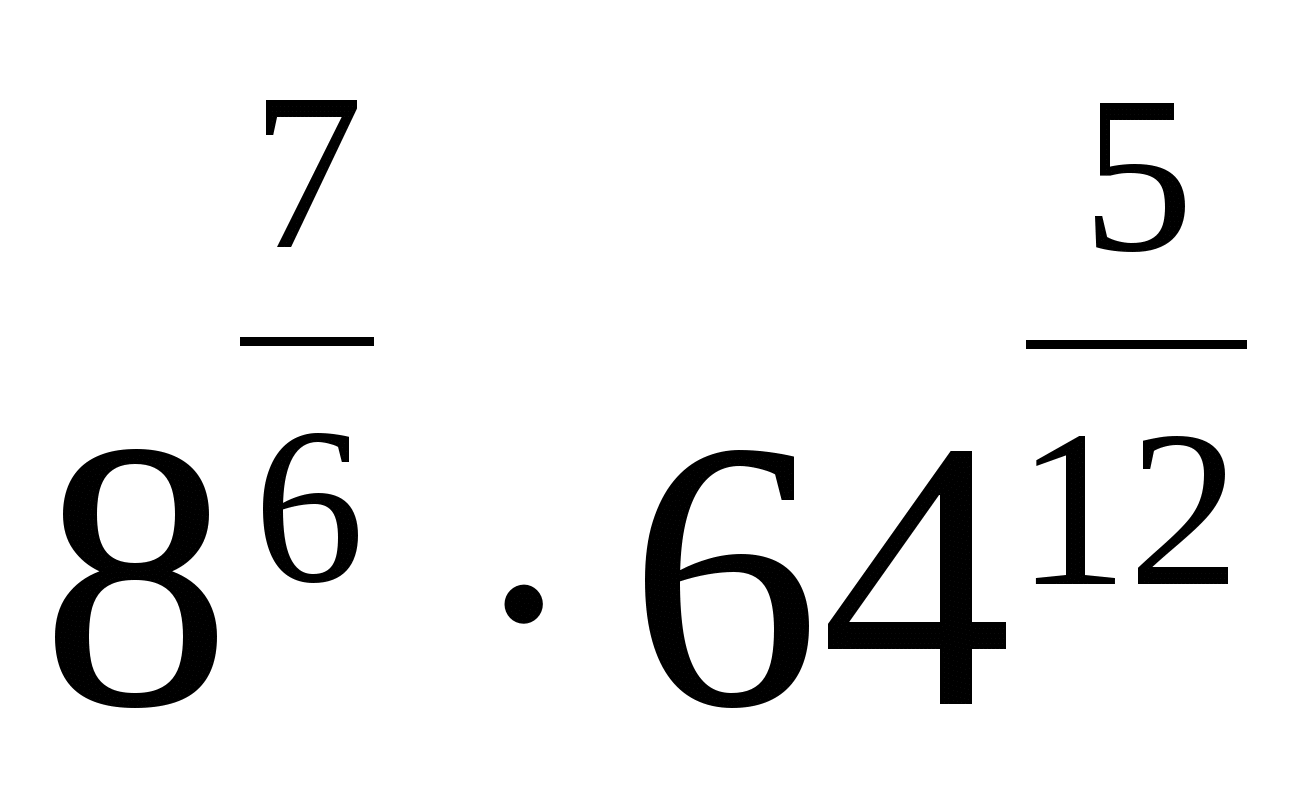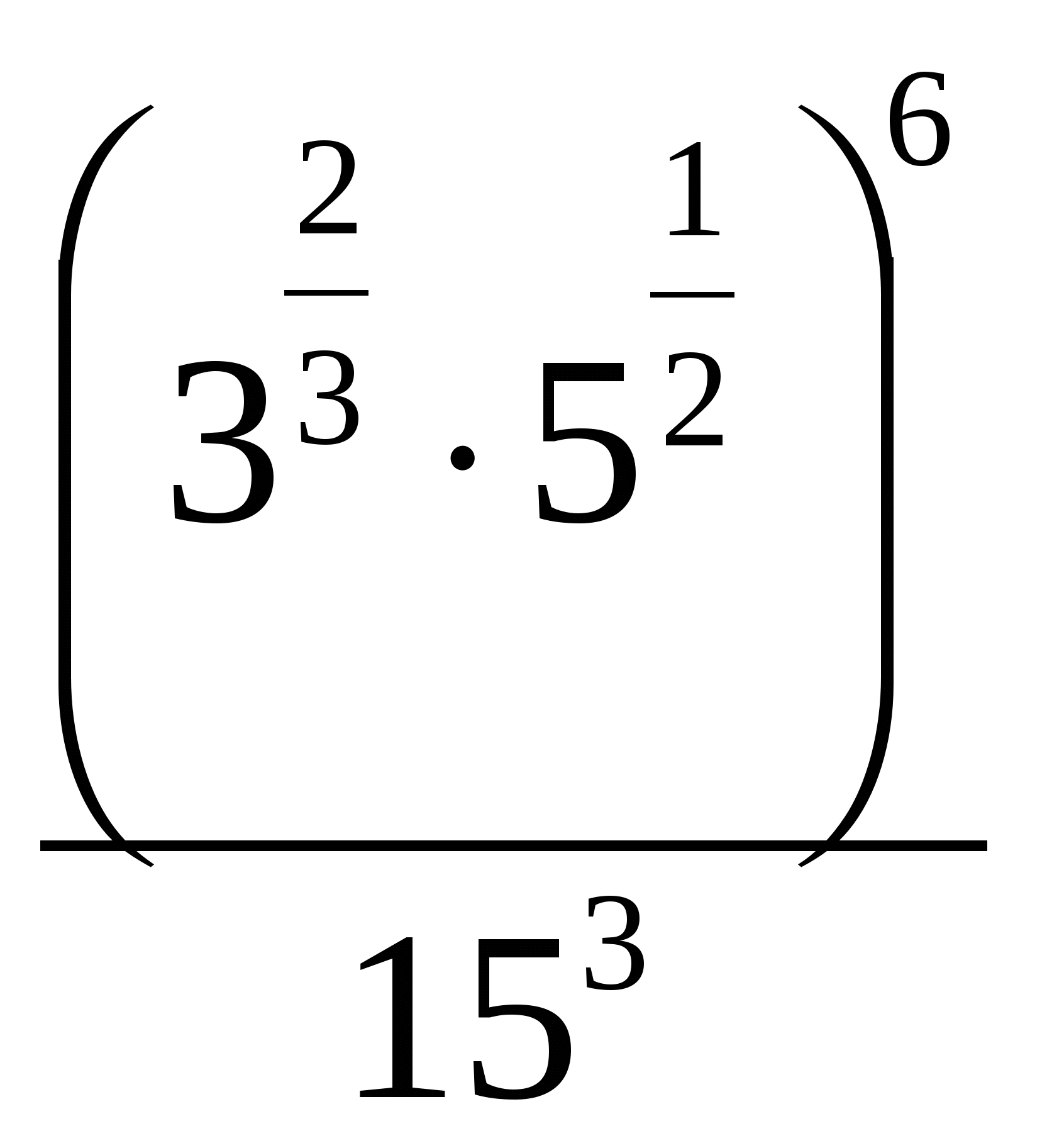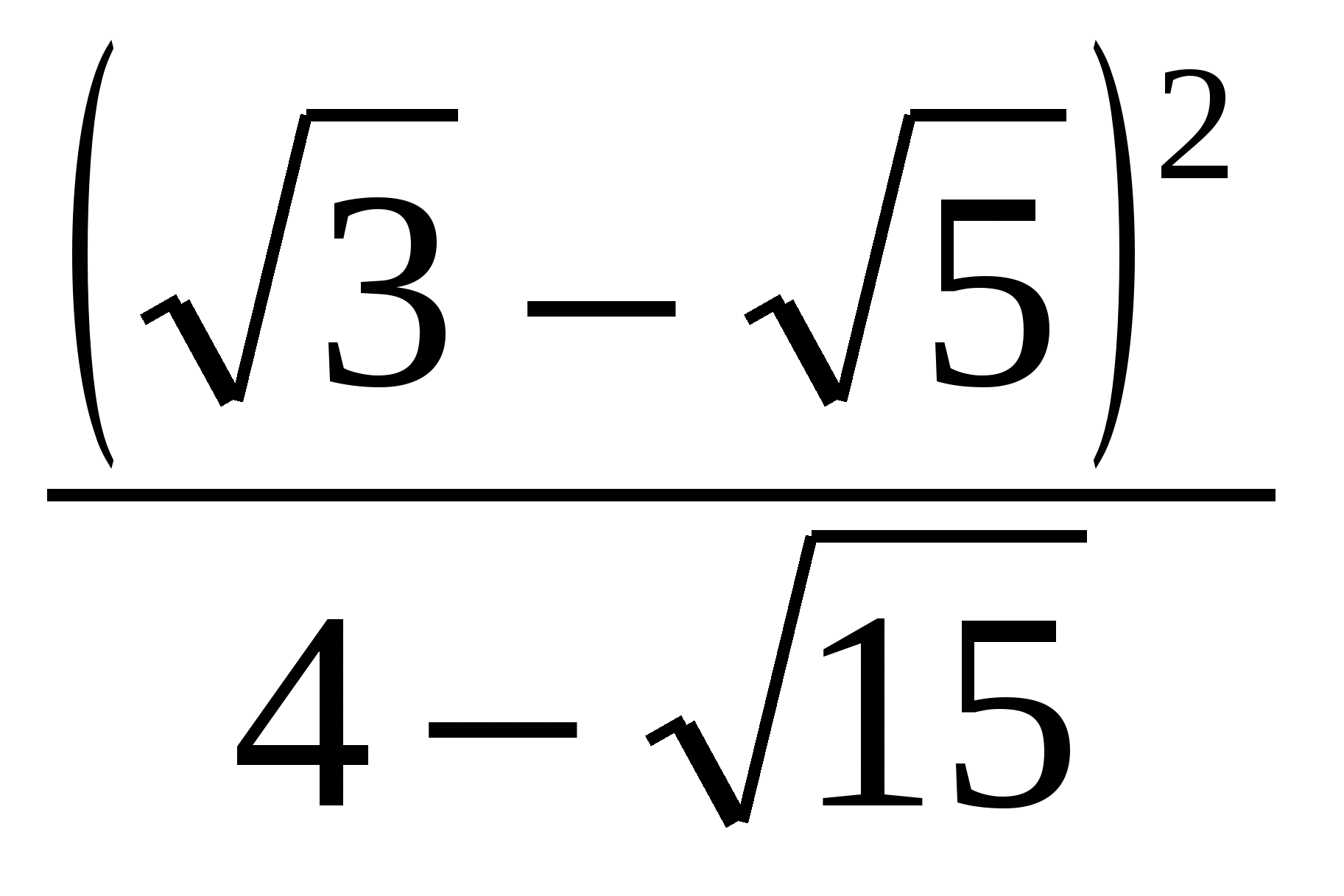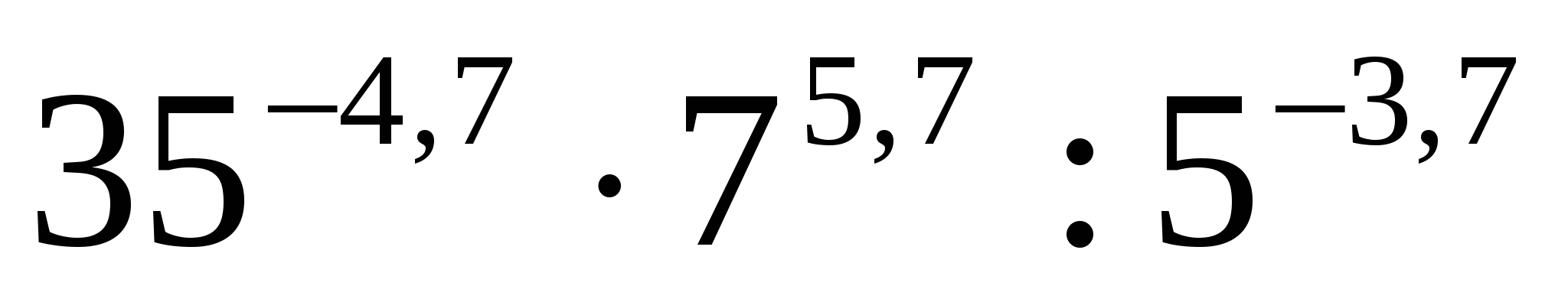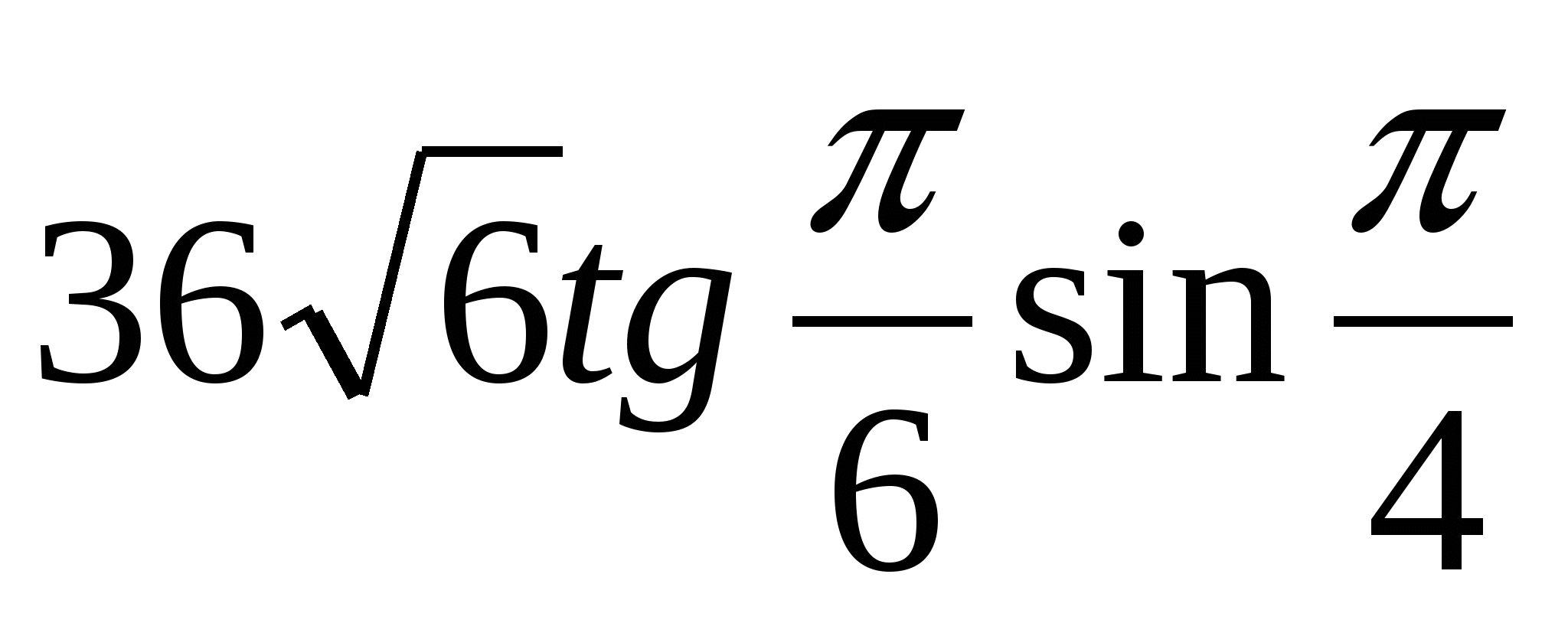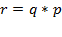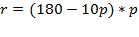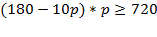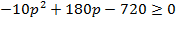В прямоугольном треугольнике случайно выбирается вершина найдите вероятность того что прямого угла
В прямоугольном треугольнике случайно выбирается вершина?
В прямоугольном треугольнике случайно выбирается вершина.
Найдите вероятность того, что выбрана вершина прямого угла.
Угол при вершине равнобедренного треугольника на 30 больше угла при основании найдите все углы треугольника?
Угол при вершине равнобедренного треугольника на 30 больше угла при основании найдите все углы треугольника.
Острые углы прямоугольного треугольника равны 84 и 6?
Острые углы прямоугольного треугольника равны 84 и 6.
Найдите угол между высотой и биссекрисой, проведенными из вершины прямого угла.
Острые углы прямоугольного треугольника равны 29о и 61о?
Острые углы прямоугольного треугольника равны 29о и 61о.
Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла.
Ответ дайте в градусах.
В прямоугольном треугольнике угол между высотой и биссектрисой проведенными из вершины прямого угла, равен 2?
В прямоугольном треугольнике угол между высотой и биссектрисой проведенными из вершины прямого угла, равен 2.
Найдите меньший угол данного треугольника.
Ответ дайте в градусах.
В прямоугольном треугольнике, катеты которого равны 8 и 6, из вершины прямого угла на гипотенузу опущена высота?
В прямоугольном треугольнике, катеты которого равны 8 и 6, из вершины прямого угла на гипотенузу опущена высота.
Найдите разность между площадями большего и меньшего треугольников, на которые высота делит заданный треугольник.
Найдите меньший угол прямоугольного треугольника.
Ответ дайте в градусах.
Высота прямоугольного треугольника проведённая из вершины прямого угла равна 17 см какую длину не может иметь гипотенуза этого треугольника?
Высота прямоугольного треугольника проведённая из вершины прямого угла равна 17 см какую длину не может иметь гипотенуза этого треугольника.
В прямоугольном треугольнике угол между высотой и медианой, проведёнными из вершины прямого угла, равен 39?
В прямоугольном треугольнике угол между высотой и медианой, проведёнными из вершины прямого угла, равен 39.
Найдите меньший из углов треугольника.
Высота прямоугольного треугольника проведенная из вершины прямого угла к гипотенузе, равна 2 √5?
Высота прямоугольного треугольника проведенная из вершины прямого угла к гипотенузе, равна 2 √5.
Полное решение надо
(СЛУЧАЙНО ПОСТАВИЛ АЛГЕБРА!
В прямоугольном треугольнике АВС с прямым углом С, АВ = 17, tgA = 5 / 3?
В прямоугольном треугольнике АВС с прямым углом С, АВ = 17, tgA = 5 / 3.
В прямоугольном треугольнике случайно выбирается вершина. Найдите вероятность того, что.
В 4:23 поступил вопрос в раздел Алгебра, который вызвал затруднения у обучающегося.
Вопрос вызвавший трудности
В прямоугольном треугольнике случайно выбирается вершина. Найдите вероятность того, что выбрана вершина прямого угла
Ответ подготовленный экспертами Учись.Ru
Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «Алгебра». Ваш вопрос звучал следующим образом:
В прямоугольном треугольнике случайно выбирается вершина. Найдите вероятность того, что выбрана вершина прямого угла
После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:
НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:
Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.
ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!
Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.
Деятельность компании в цифрах:
Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.
Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.
В прямоугольном треугольнике случайно выбирается вершина найдите вероятность того что прямого угла
В прямоугольном треугольнике угол между высотой и медианой, проведёнными из вершины прямого угла, равен 38°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
В прямоугольном треугольнике CHM угол C равен 38°, поэтому угол M равен 52°. Треугольник АСВ прямоугольный, CM — медиана, опущенная из вершины прямого угла, следовательно, CM = MB, и углы B и MCB равны как углы при основании равнобедренного треугольника. Тогда:
В прямоугольном треугольнике угол между высотой и медианой, проведёнными из вершины прямого угла, равен 26°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
В прямоугольном треугольнике CHM угол C равен 26°, поэтому угол M равен 64°. Треугольник АСВ прямоугольный, CM — медиана, опущенная из вершины прямого угла, следовательно, CM = MB, и углы B и MCB равны как углы при основании равнобедренного треугольника. Тогда:
В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
Это задание ещё не решено, приводим решение прототипа.
В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
В прямоугольном треугольнике CHM угол C равен 40°, поэтому угол M равен 50°. Треугольник АСВ прямоугольный, CM — медиана, опущенная из вершины прямого угла, следовательно, CM = MB, и углы B и MCB равны как углы при основании равнобедренного треугольника. Тогда:
В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
Это задание ещё не решено, приводим решение прототипа.
В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
В прямоугольном треугольнике CHM угол C равен 40°, поэтому угол M равен 50°. Треугольник АСВ прямоугольный, CM — медиана, опущенная из вершины прямого угла, следовательно, CM = MB, и углы B и MCB равны как углы при основании равнобедренного треугольника. Тогда:
В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
Это задание ещё не решено, приводим решение прототипа.
В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
В прямоугольном треугольнике CHM угол C равен 40°, поэтому угол M равен 50°. Треугольник АСВ прямоугольный, CM — медиана, опущенная из вершины прямого угла, следовательно, CM = MB, и углы B и MCB равны как углы при основании равнобедренного треугольника. Тогда:
В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
Это задание ещё не решено, приводим решение прототипа.
В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
В прямоугольном треугольнике CHM угол C равен 40°, поэтому угол M равен 50°. Треугольник АСВ прямоугольный, CM — медиана, опущенная из вершины прямого угла, следовательно, CM = MB, и углы B и MCB равны как углы при основании равнобедренного треугольника. Тогда:
Введение
Интенсивный курс по подготовке к ЕГЭ предназначен для подготовк и учащихся старших классов к успешной сдаче ЕГЭ по математике в 2014 году. С 2014 года в контрольно- измерительн ые материал ы по математике внесены изменения. Экзамен первой части В состоит из 15 заданий. Данный курс состоит из первой части В. Каждое задание состоит из теоретического материала: формул, правил и образцов решений заданий. К каждой теме подобраны типичные задания из открытого банка ЕГЭ для самостоятельного решения.
Теоретический материал и решенные задания изложены в доступной и краткой форме. Даже слабый ученик может пользоваться данным пособием.
Данный материал можно ис пользовать на уроке при повторении тем, для дополнительных занятий и для элективных курсов.
В1 Практико-ориентированные задачи 1
1. В летнем лагере на каждого участника полагается 70 г сахара в день. В лагере 172 человека. Какого наименьшего количества килограммовых пачек сахара достаточно на 7 дней?
1) Нужно узнать сколько граммов сахара полагается 172 человека в день: 172·70 = 12 040 г
2) Сколько будет на 7 дней: 12040 · 7 = 84 280г
3) Сколько будет килограммовых пачек: 84 280:1 000 = 84 кг 280г
4) Если будет 84 пачек, то нехватит 280 г, по этому берем 85 пачек Ответ 85
1 Больному прописано лекарство, которое нужно пить по 0,5 г 4 раза в день в течение 7 дней. Лекарство выпускается в упаковках по 8 таблеток по 0,25 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
2 На день рождения полагается дарить букет из нечетного числа цветов. Тюльпаны стоят 30 руб. за штуку. У Вани есть 450 руб. Из какого наибольшего числа тюльпанов он может купить букет Маше на день рождения?
3 В летнем лагере 230 детей и 27 воспитателей. В автобус помещается не более 49 пассажиров. Сколько автобусов требуется, чтобы перевезти всех из лагеря в город?
4 В супермаркете проходит рекламная акция: покупая 2 шоколадки, 3-ю шоколадку покупатель получает в подарок. Шоколадка стоит 35 рублей. Какое наибольшее число шоколадок получит покупатель на 200 рублей?
5 Для приготовления маринада для огурцов на 1 литр воды требуется 16 г лимонной кислоты. Хозяйка готовит 6 литров маринада. В магазине продаются пачки лимонной кислоты по 10 г. Какое наименьшее число пачек нужно купить хозяйке для приготовления маринада?
6 Аня купила месячный проездной билет на автобус. За месяц она сделала 44 поездки. Сколько рублей она сэкономила, если проездной билет стоит 600 рублей, а разовая поездка 20 рублей?
7 В пачке бумаги 250 листов формата А4. За неделю в офисе расходуется 1700 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 3 недели?
8. На автозаправке клиент отдал кассиру 1000 рублей и попросил залить бензин до полного бака. Цена бензина 31 руб. 20 коп. Сдачи клиент получил 1 руб. 60 коп. Сколько литров бензина было залито в бак?
9. В квартире, где проживает Алексей, установлен прибор учёта расхода холодной воды (счётчик). 1 сентября счётчик показывал расход 103 куб.м воды, а 1 октября — 114 куб.м. Какую сумму должен заплатить Алексей за холодную воду за сентябрь, если цена 1 куб.м холодной воды составляет 19 руб. 20 коп.? Ответ дайте в рублях.
10.В университетскую библиотеку привезли новые учебники по геометрии для 3 курсов, по 360 штук для каждого курса. Все книги одинаковы по размеру. В книжном шкафу 9 полок, на каждой полке помещается 25 учебников. Сколько шкафов можно полностью заполнить новыми учебниками?
11.На счету Машиного мобильного телефона было 53 рубля, а после разговора с Леной осталось 8 рублей. Сколько минут длился разговор с Леной, если одна минута разговора стоит 2 рубля 50 копеек.
12.Выпускники 11 «А» покупают букеты цветов для последнего звонка: из 3 роз каждому учителю и из 7 роз классному руководителю и директору. Они собираются подарить букеты 15 учителям (включая директора и классного руководителя), розы покупаются по оптовой цене 35 рублей за штуку. Сколько рублей стоят все розы?
13.Поезд Новосибирск-Красноярск отправляется в 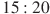
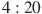
14.В школе есть трехместные туристические палатки. Какое наименьшее число палаток нужно взять в поход, в котором участвует 20 человек?
15.В общежитии института в каждой комнате можно поселить четырех человек. Какое наименьшее количество комнат необходимо для поселения 83 иногородних студентов?
16.Каждый день во время конференции расходуется 70 пакетиков чая. Конференция длится 6 дней. Чай продается в пачках по 50 пакетиков. Сколько пачек нужно купить на все дни конференции?
17.В доме, в котором живет Петя, один подъезд. На каждом этаже по шесть квартир. Петя живет в квартире 50. На каком этаже живет Петя?
18.Спидометр автомобиля показывает скорость в милях в час. Какую скорость (в милях в час) показывает спидометр, если автомобиль движется со скоростью 36 км в час? (Считайте, что 1 миля равна 1,6 км.)
19.Для ремонта квартиры требуется 63 рулона обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 6 рулонов?
20.В розницу один номер еженедельного журнала стоит 24 рубля, а полугодовая подписка на этот журнал стоит 460 рублей. За полгода выходит 25 номеров журнала. Сколько рублей можно сэкономить за полгода, если не покупать каждый номер журнала отдельно, а получать журнал по подписке?
21.Установка двух счётчиков воды (холодной и горячей) стоит 3300 рублей. До установки счётчиков Александр платил за воду (холодную и горячую) ежемесячно 800 рублей. После установки счётчиков оказалось, что в среднем за месяц он расходует воды на 300 рублей при тех же тарифах на воду. За какое наименьшее количество месяцев при тех же тарифах на воду установка счётчиков окупится?
В2 Задачи на проценты
Чтобы найти процент от данного числа, нужно перевести процент в десятичную дробь и умножить на данное число.
Пример: Найти 35% от числа 120. Решение: 35%=0,35 120∙0,35=42
Чтобы найти число по данному значению его процента, надо перевести процент в десятичную дробь и это значение разделить на дробь.
Пример: 70% от данного числа составляет 21. Найти данное число.
Решение: 70%=0,7 21:0,7=210:7=30
Задача: Флакон шампуня стоит 200 рублей Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 15%?
1) Сколько рублей составит 15%: 15% = 0,15 200 · 0,15 = 30р
2) 30 р это количество скидки, тогда 200 – 30 = 170р стоимость флакона шампуня после скидки.
3) Чтобы узнать сколько флаконов можно купить на 1000р: 1000 : 170 = 5 ( остаток 150) 150р сдача
1 Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена цена на футболку?
2 Цена на электрический чайник была повышена на 21% и составила 3025 рублей. Сколько рублей стоил товар до повышения цены?
3 Магазин закупает цветочные горшки по оптовой цене 90 рублей за штуку. Торговая наценка составляет 15%. Какое наибольшее число таких горшков можно купить в этом магазине на 700 рублей?
4 В городе N живет 200000 жителей. Среди них 10 % детей и подростков. Среди взрослых 45% не работает (пенсионеры, домохозяйки, безработные). Сколько взрослых работает?
5. Держатели дисконтной карты книжного магазина получают при покупке скидку 5%. Книга стоит 200 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
6. При оплате услуг через платежный терминал взимается комиссия 5%. Терминал принимает суммы кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не меньше 300 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала?
7. В сентябре 1 кг винограда стоил 60 рублей, в октябре виноград подорожал на 25%, а в ноябре еще на 20%. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?
8. Мобильный телефон стоил 3500 рублей. Через некоторое время цену на эту модель снизили до 2800 рублей. На сколько процентов была снижена цена?
В3 Чтение графиков
1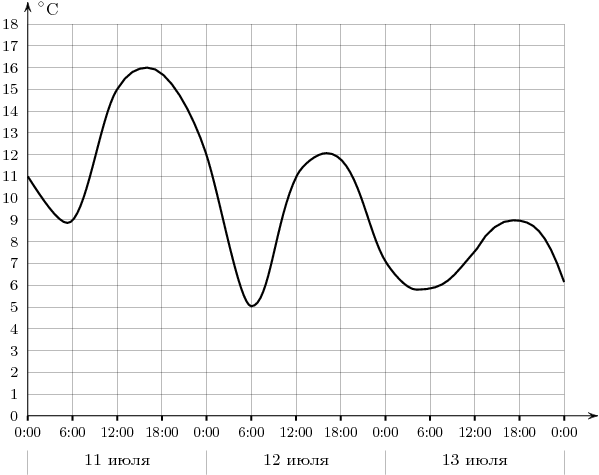
Решение : 1) Рассмотрим график только на третьи сутки то есть 13 июля с 0:00 до 0:00 следующего дня
2
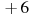
2) На оси ординат найдем +6 º и по оси абцисс определим сколько дней график функции выше или равно 6 º
это от 9 до 19, значит 10 дней. Ответ: 10
1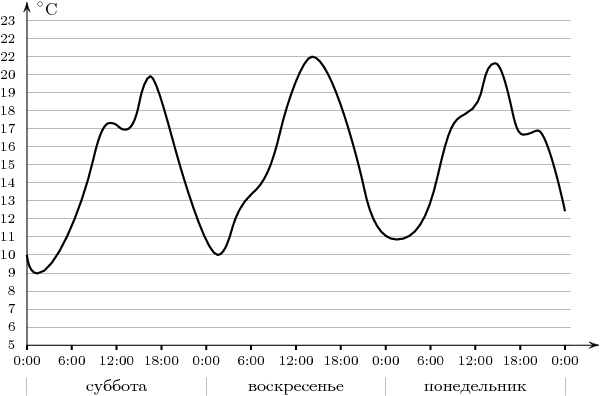
2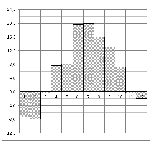
В4 Практико-ориентированные задачи 2
1. Телефонная компания предоставляет на выбор три тарифных плана.
Плата за 1 минуту разговора
200 р. за 360 минут в месяц
Свыше 360 минут в месяц — 0,4 р. за каждую минуту.
Абонент выбрал наиболее дешевый тарифный план, исходя из предположения, что общая длительность телефонного разговора составляет 700 минут в месяц. Какую сумму он должен заплатить за месяц, если общая длительность разговоров в этом месяце действительно будет равна 700 мин? Ответ дайте в рублях.
Решение: 1 тариф: 700·0,5 = 350 р в месяц
2 тариф: за 360 мин 200р. а за 340мин: 340·0,4 = 136р всего: 336р в месяц
3 тариф: 397р в месяц Ответ: 350
Решение: 1 каменный: 8 · 1600 = 12 800р 8 · 250 = 2 000р всего 12800+2000 = 14 800р
2 бетонный: 6 · 690 = 4 140р 43 · 250 = 10 750р всего 4140+10750 = 14 890р
1. Строительной фирме нужно приобрести 73 кубометров пенобетона. У неё есть 3 поставщика. Сколько рублей придется заплатить за самую дешевую покупку с доставкой? Цены и условия доставки приведены в таблице
Стоимость пенобетона (р. за м3 )
При заказе на сумму больше 150000 р. доставка бесплатно
При заказе более 75 м3 доставка бесплатно
2. Для изготовления книжных полок требуется заказать 20 одинаковых стекол в одной из трех фирм. Площадь каждого стекла 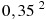
Стоимость стекла
(руб. за 1 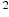
Резка и шлифовка
(руб. за одно стекло)
3. Семья из трех человек едет из Москвы в г.Чебоксары. Можно ехать поездом, а можно — на своей машине. Билет на поезд стоит 850 рублей на одного человека. Автомобиль расходует 15 литров бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина равна 20 руб. за литр. Сколько рублей придется заплатить за наиболее дешевую поездку на троих?
Стоимость перевозки одним автомобилем (р. на 100 км)
Грузоподъемность автомобилей (тонн)
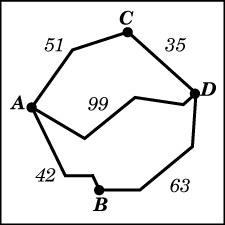
5. Из пункта А в пункт D ведут три дороги. Через пункт В едет грузовик со средней скоростью 42 км/ч, через пункт С едет автобус со средней скоростью 43 км/ч. Третья дорога — без промежуточных пунктов, и по ней движется легковой автомобиль со средней скоростью 66 км/ч. На рисунке показана схема дорог и расстояние между пунктами по дорогам.
Все три автомобиля одновременно выехали из А. Какой автомобиль добрался до D позже других? В ответе укажите, сколько часов он находился в дороге.
7. В таблице даны оценки каждого показателя для нескольких новостных сайтов. Определите наивысший рейтинг новостных сайтов, представленных в таблице. Запишите его в ответ, округлив до целого числа.
8. В среднем гражданин А. в дневное время расходует 120 кВт 




10. При строительстве сельского дома можно использовать один из двух типов фундамента: каменный или бетонный. Для каменного фундамента необходимо 9 тонн природного камня и 9 мешков цемента. Для бетонного фундамента необходимо 7 тонн щебня и 50 мешков цемента. Тонна камня стоит 1600 рублей, щебень стоит 780 рублей за тонну, а мешок цемента стоит 230 рублей. Сколько рублей будет стоить материал для фундамента, если выбрать наиболее дешевый вариант?
Процент от выручки, поступающий в доход салона
Изделия ценой до 
Изделия ценой свыше 
В прейскуранте приведены цены на четыре дивана. Определите, продажа какого дивана наиболее выгодна для салона. В ответ запишите, сколько рублей поступит в доход салона от продажи этого дивана.
Задания В 5 : Площад и плоских фигур
Ф
S = a · b S = a · h 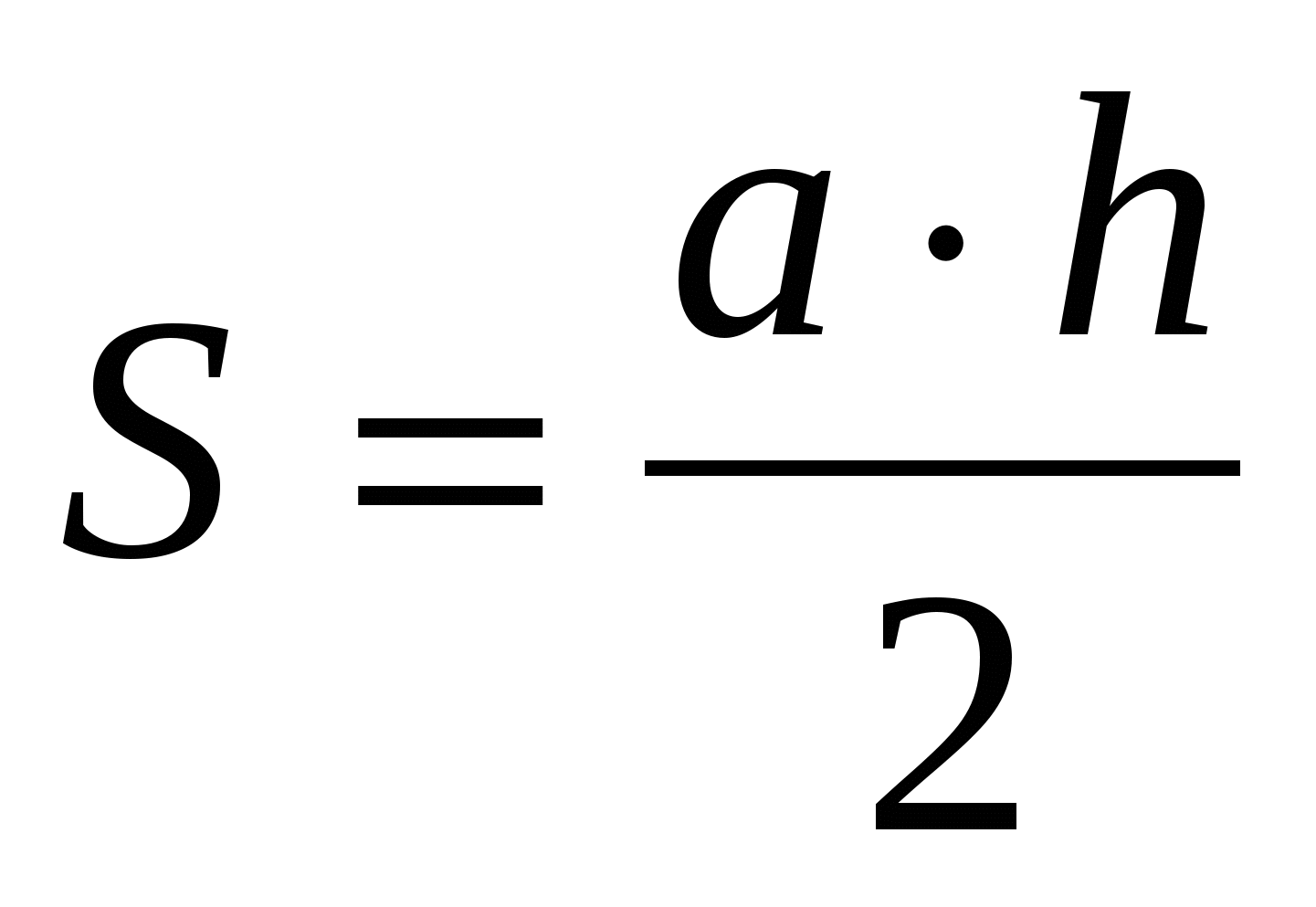
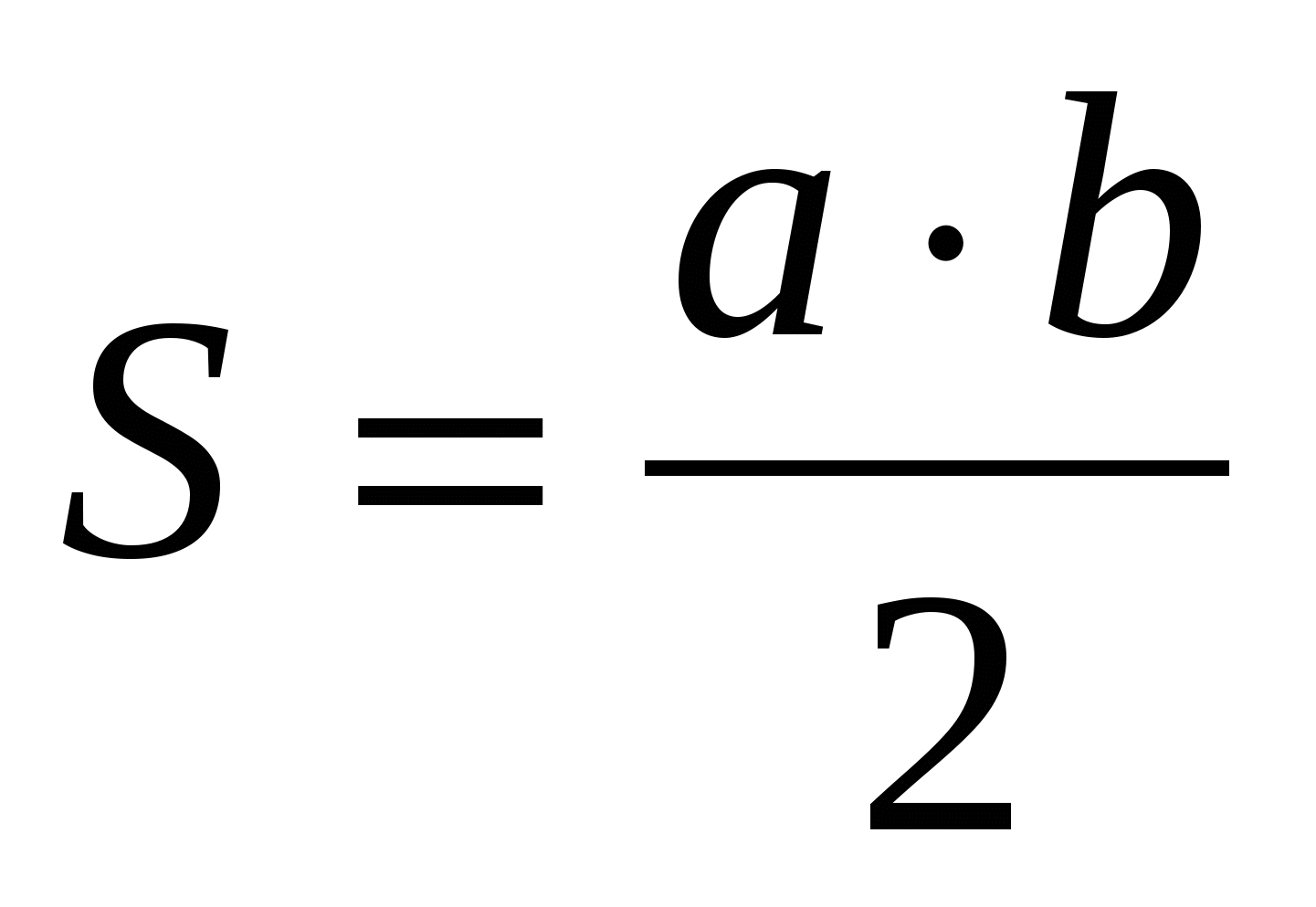

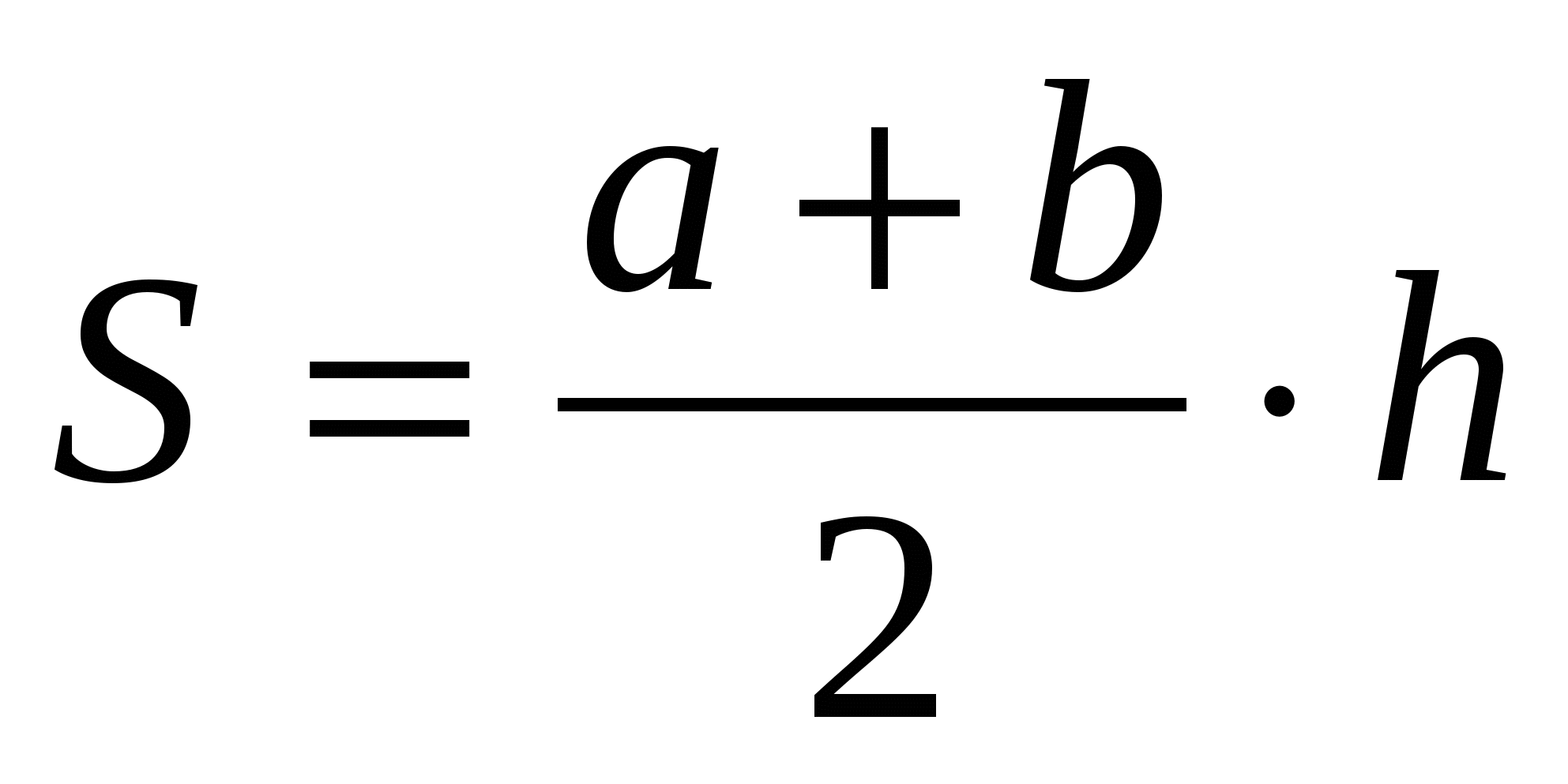
1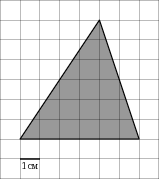

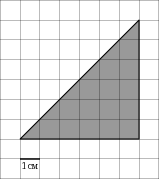
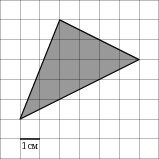
2. На клетчатой бумаге с клетками размером 1 см 
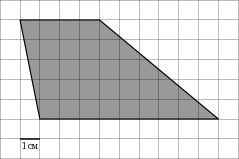
3. На клетчатой бумаге с клетками размером 1 см 
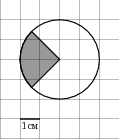
4. На клетчатой бумаге с клетками размером 1 см 
5. На клетчатой бумаге с клетками размером 1 см 
6. На клетчатой бумаге с клетками размером 1 см 

7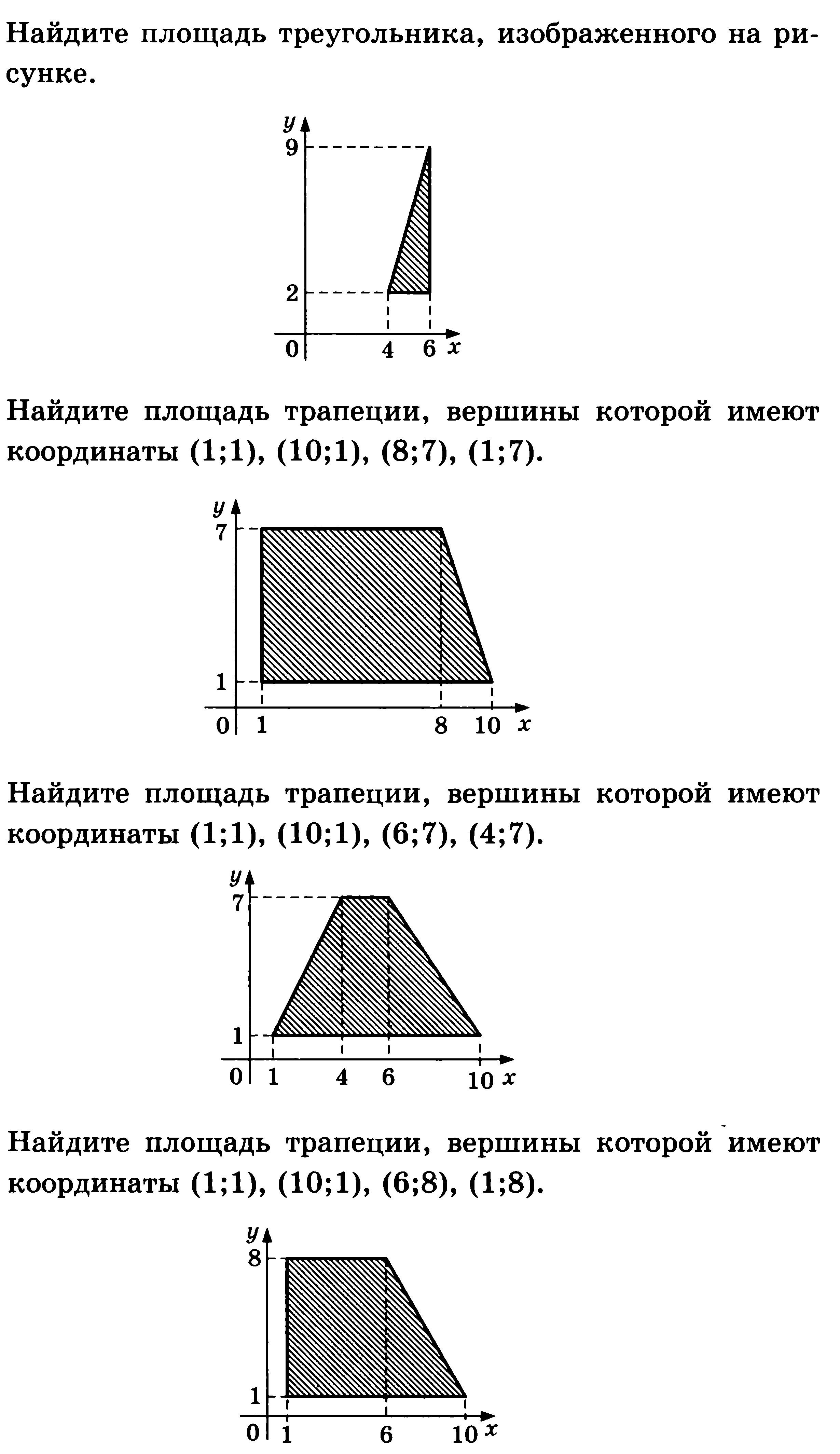
8. Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (8;7), (1;7)
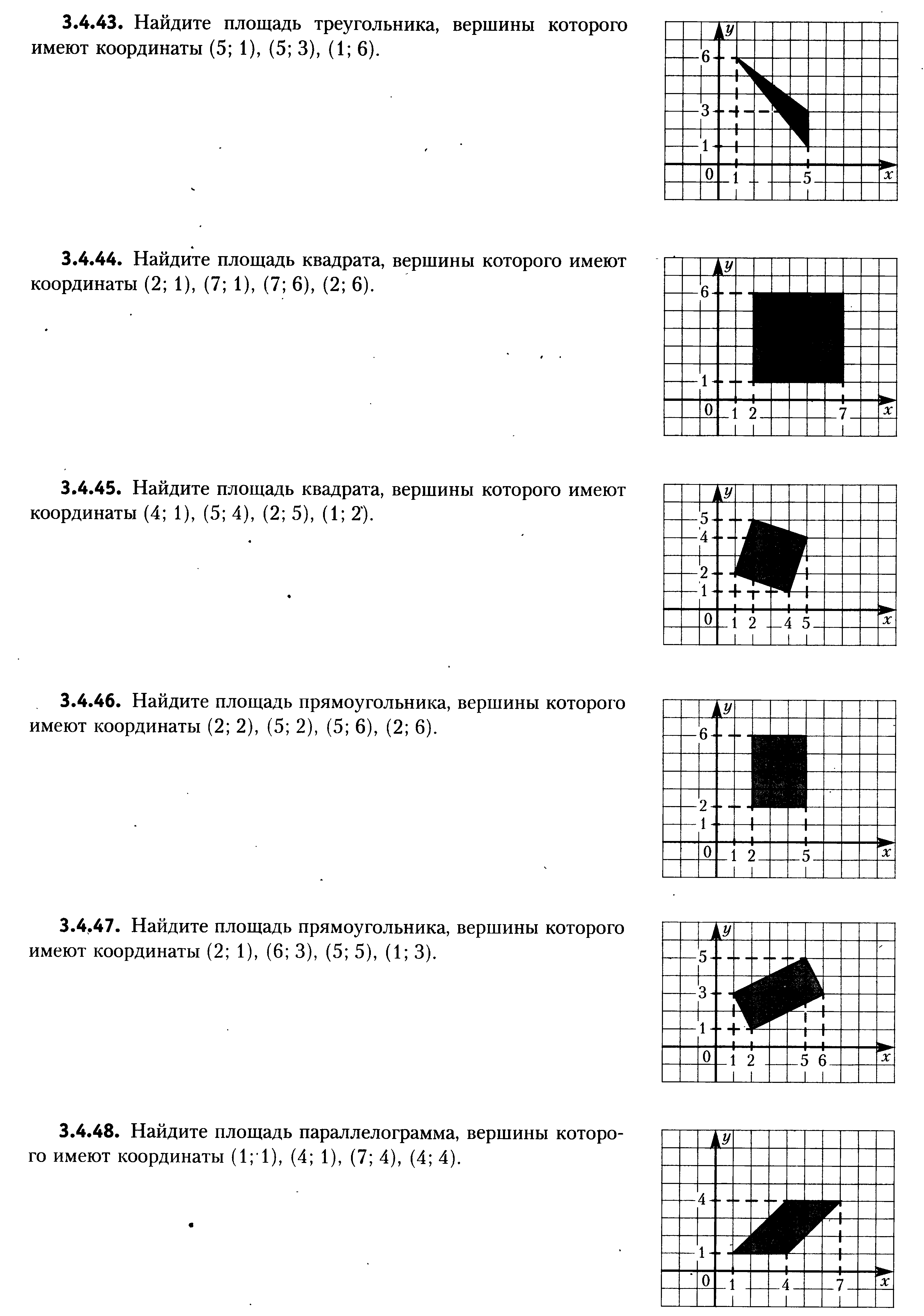
9. Найдите площадь треугольника, вершины которого имеют координаты (5;1), (5;3), (1;6)
10. Найдите площадь параллелограмма, вершины которого имеют координаты (1;1), (4;1), (7;4), (4;4)
В6 : Т еори я вероятностей
Определить в чем состоит случайный эксперимент и какие у него элементарные события (исходы). Убедится, что они равновозможны.
Определить какие элементарные события благоприятствуют интересующему нас событию А, и найти их число N (А).
Найти вероятность событий А по формуле Р(А) =
1. Вася, Петя, Коля и Лёша бросили жребий – кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.
Решение. Случайный эксперимент – бросание жребия. Элементарное событие в этом эксперименте – участник, который вы и грал жребий. Перечислим их: (Вася), (Петя), (Коля) и (Леша). Общее число элементарных событий N равно 4. Жребий подразумевает, что элементарные события равновозможны. Событию А= <жребий выйграл Петя>благоприятствует только одно элементарное событие (Петя). Поэтому N( A )=1. Тогда 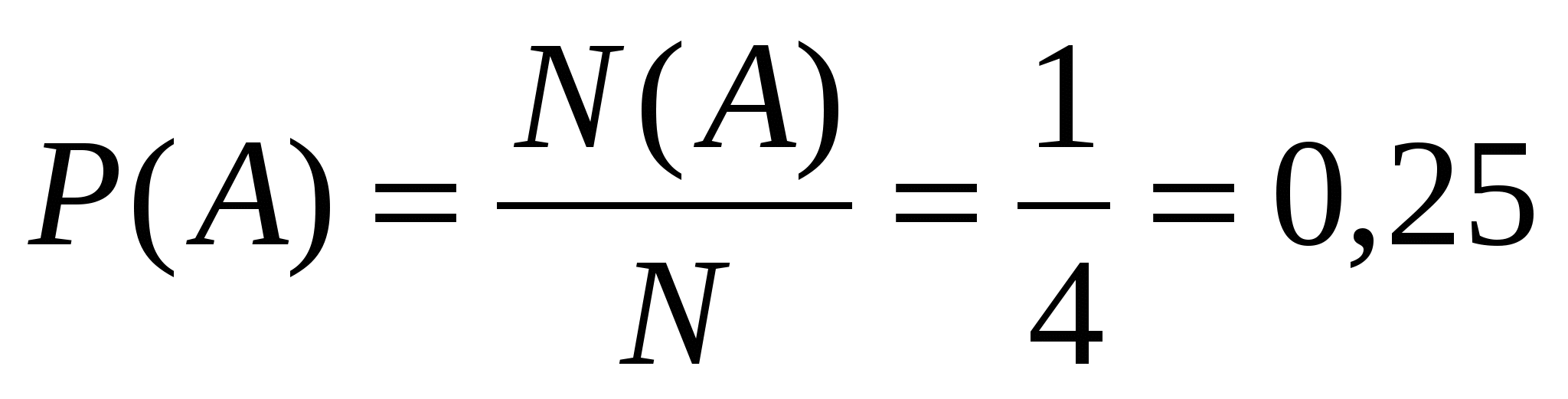
Решение. Здесь случайный эксперимент – бросание кубика. Элементарное событие – число выпавшей грани. Граней всего шесть. Перечислим все элементарные события: 1, 2, 3, 4, 5 и 6. Значит, N=6.
Событию А= <выпало больше чем 4>благоприятствуют два элементарных события: 5 и 6. Поэтому N( A )=2. Элементарные события равновозможны, поскольку подразумевается, что кубик честный. Поэтому
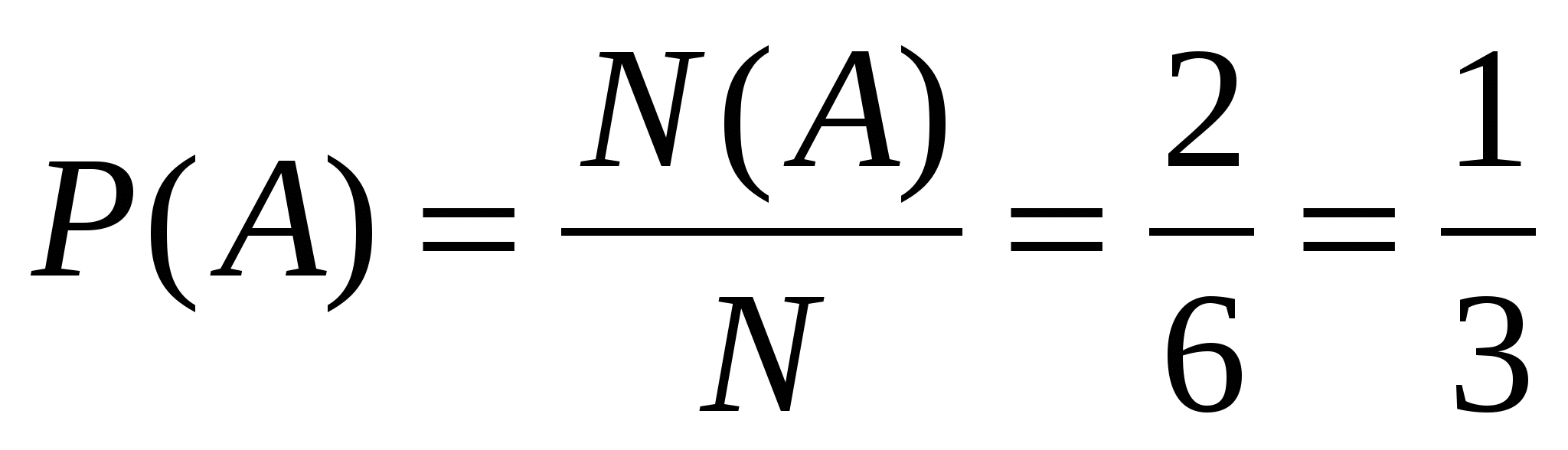
1.В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Решение: Элементарный исход в это опыте – упорядоченная пара чисел. Первое число выпадает на первом кубике, а второе – на втором. Множествотэлементарных исходов удобно представить таблицей. Строки соответствуют результату первого броска, столбцы – результату второго броска. Всего элементарных событий N =36.
Сумма выпавших очков равное 8 таких пять, значит событию А благоприятствует пять элементарных исходов. Следовательно, N (А) = 5. Поэтому 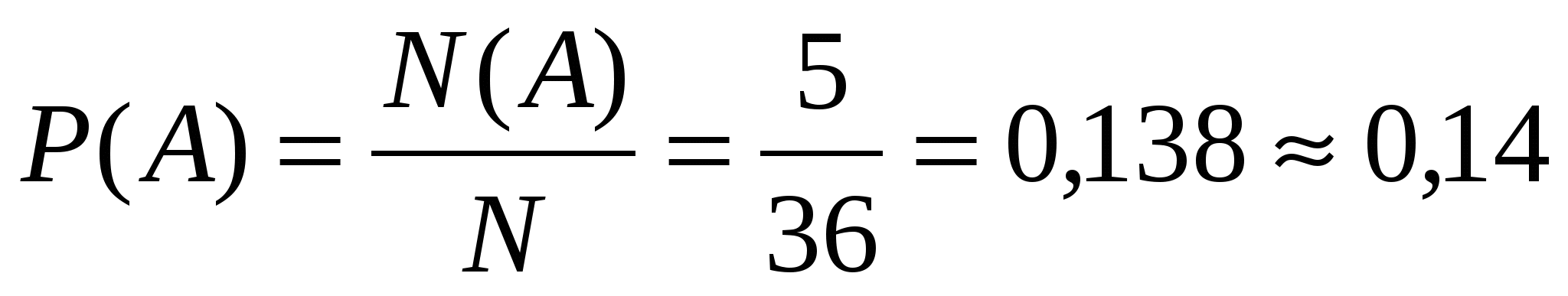
3. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадает ровно один раз.
Решение. Орел обозначим одной буквой О. Решку – буквой Р. В описанном эксперименте могут быть следующие элементарные сходы: ОО, ОР, РО и РР.
Значит, N=4. Событию А= <выпал ровно один орел>благоприятствуют элементарные события: ОР и РО. Поэтому N( A )=2. Тогда 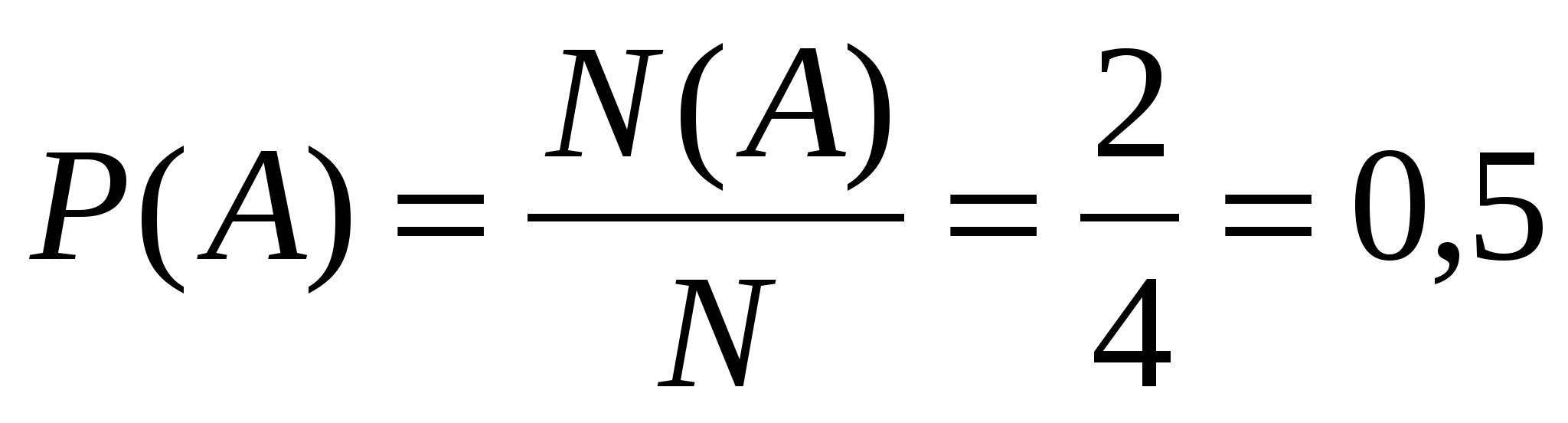
4. Максим с папой решили покататься на колесе обозрения. Всего на колесе тридцать кабинок, из них 11 – синие, 7 – зеленые, остальные – оранжевые. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Максим прокатится в оранжевой кабинке.
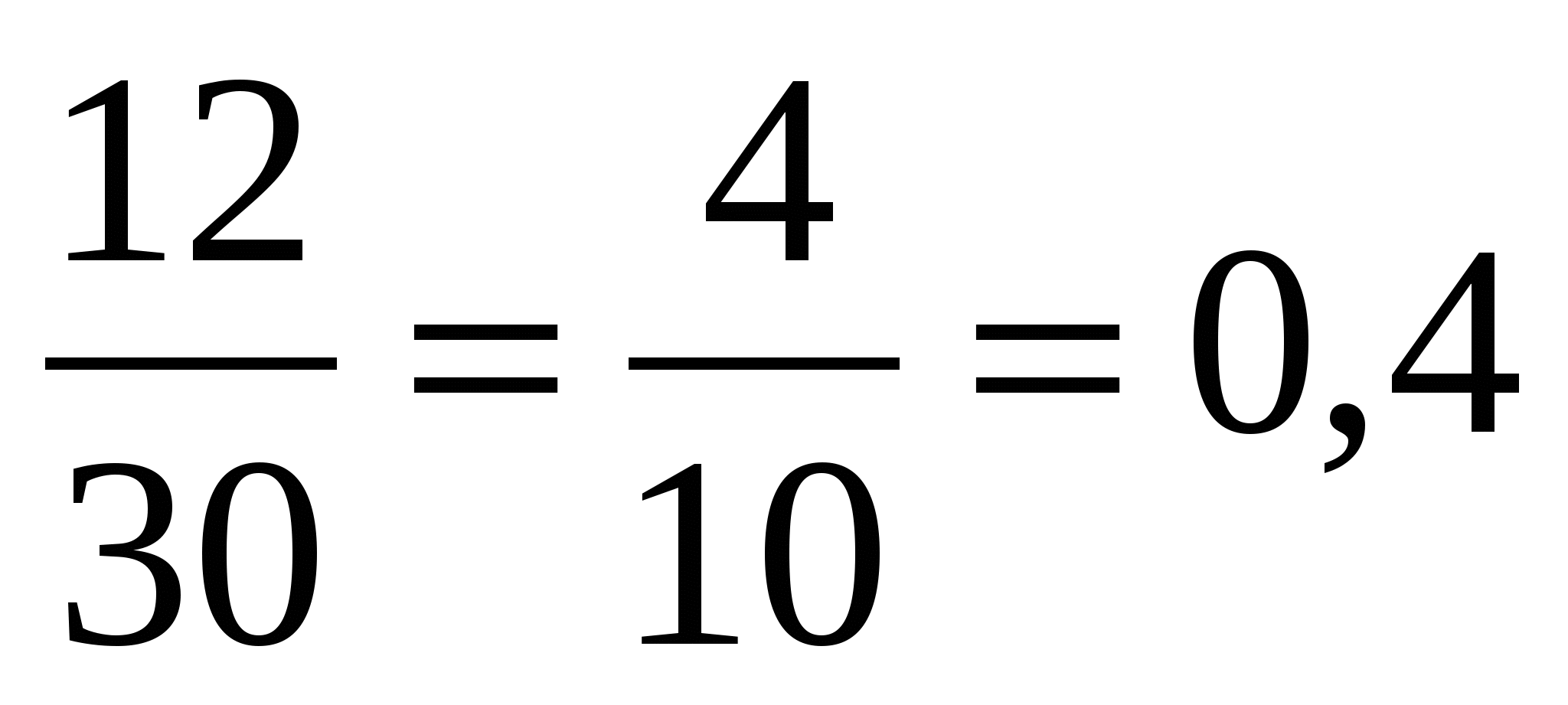
1. Игральный кубик бросают один раз один раз. Найдите вероятность того, что выпадет четное число.
10.На столе лежат 10 карточек, на которых написаны числа от 1 до 10. Миша случайно вытягивает одну карточку. С какой вероятностью число на выбранной карточке является составным?
11. Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые три дня по 15 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
12. В кармане у Миши было четыре конфеты – «Грильяж», «Белочка», «Коровка» и «Ласточка», а так же ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Грильяж».
14. На столе лежат 10 карточек, на которых написаны числа от 1 до 10. Дима случайно вытягивает одну карточку. С какой вероятностью число на выбранной карточке кратно 3?
15. Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три? 0,3
В 7 теория: Простейшие уравнения
Решение логарифмических уравнений:
Чтобы решить логарифмическое уравнение нужно:
Привести обе части уравнения к логарифму одного основания: 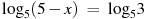
Если логарифмы равны, то подлагорифмические выражения тоже равны: 5 – х = 3
Найти ОДЗ: Подлагорифмическое выражения всегда положительны : 5 – х > 0
Решение показательных уравнений:
Чтобы решить показательные уравнения нужно:
Привести обе части уравнения к одному основанию. 4
Если основания равны, то равны их показатели степени 1 – 2х = 3
Решение иррациональных уравнений :
Чтобы решить иррациональное уравнение нужно
О бе части возвести в квадрат :
Решить уравнение: 5х – 4 = 81 
Проверить решение: 5·15 – 4 > 0
1. Решите уравнение:
2. Решите уравнение:
3. Решите уравнение:
5. Решите уравнение: (2х + 7)² = (2х – 5)²
6. Решите уравнение: х² = (х – 5)²
7. Найдите корень уравнения.
10. Найдите корень уравнения 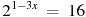
11. Найдите корень уравнения 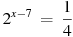
14. Найдите корень уравнения 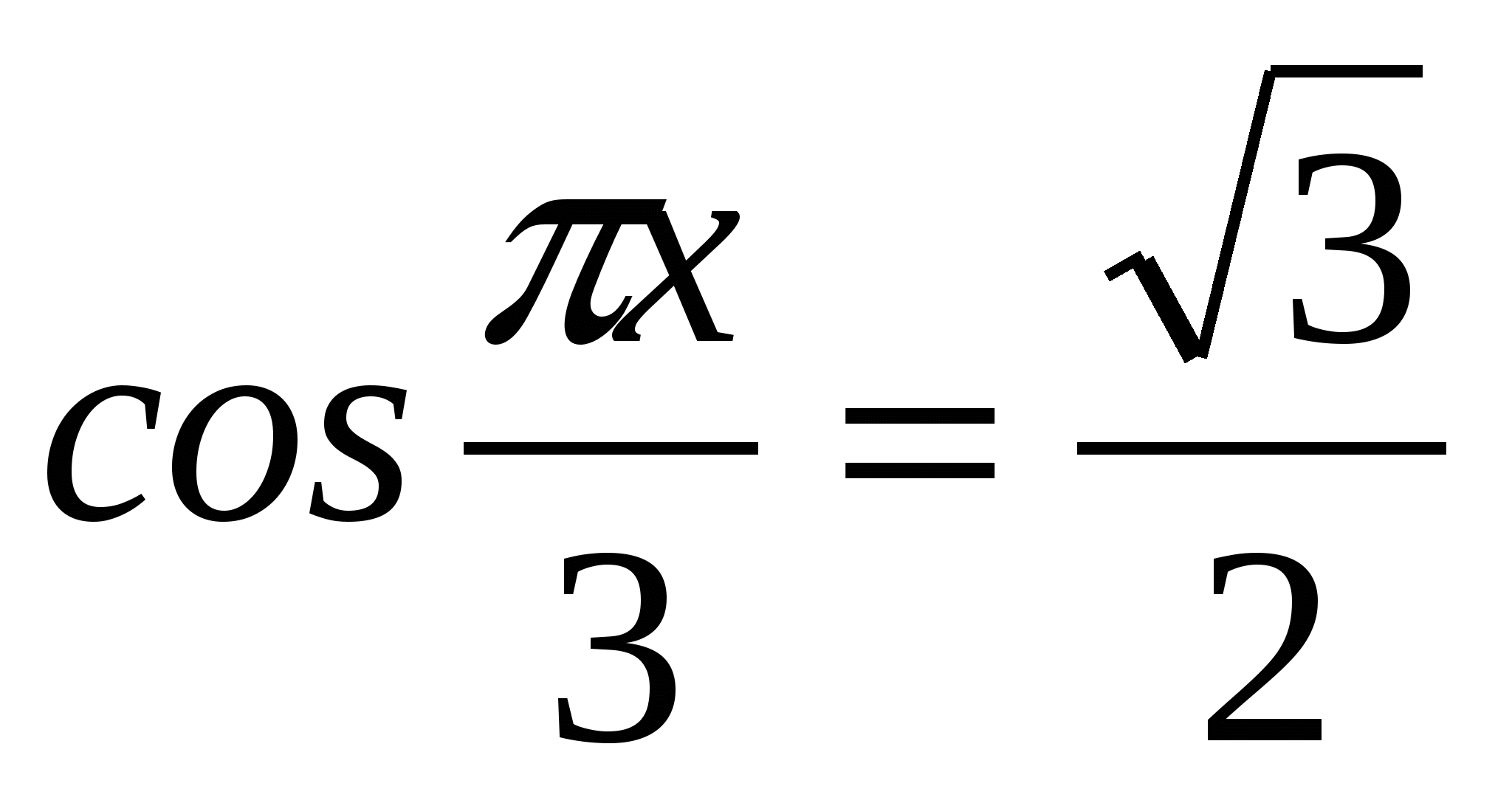
В 8 Углы на плоскости
Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.

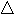
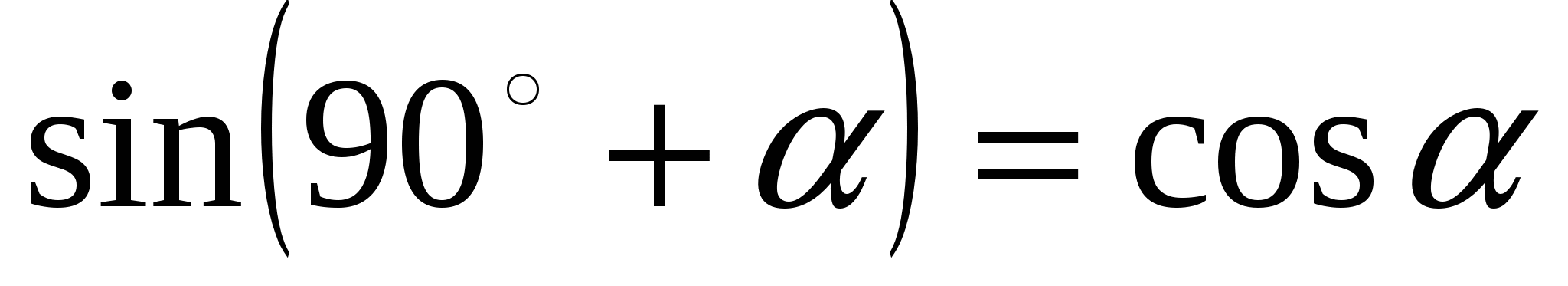
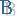
Биссектрисой треугольника, проведенной из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющей эту вершину с точкой на противолежащей стороне.
Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведенный из этой вершины к прямой, которая содержит противолежащую сторону прямоугольника.
Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны треугольника.
Углы треугольника: Сумма углов треугольника равна 180°.
Свойтво равнобедреннего треугольника: Углы равнобедренного треугольника равны.
Углы параллелограмма: Противолежащие углы равны. Сумма односторонних углов равна 180º.
Углы равнобедренной трапеции : Углы при основании ранобедренной трапеции равны.
Вписанный угол равен половине центрального угла.
1. В равнобедренном треугольнике ABC с основанием AC боковая сторона AB равна 8, а 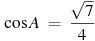
2. В равнобедренном треугольнике ABC с основанием AC боковая сторона AB равна 25, а высота, проведенная к основанию, равна 20. Найдите косинус угла 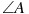
3. В треугольнике ABC угол C равен 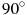
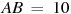
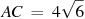
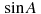
6. В треугольнике ABC угол C равен 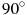
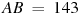
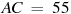
14. Найдите вписанный угол опирающийся на дугу, которая составляет 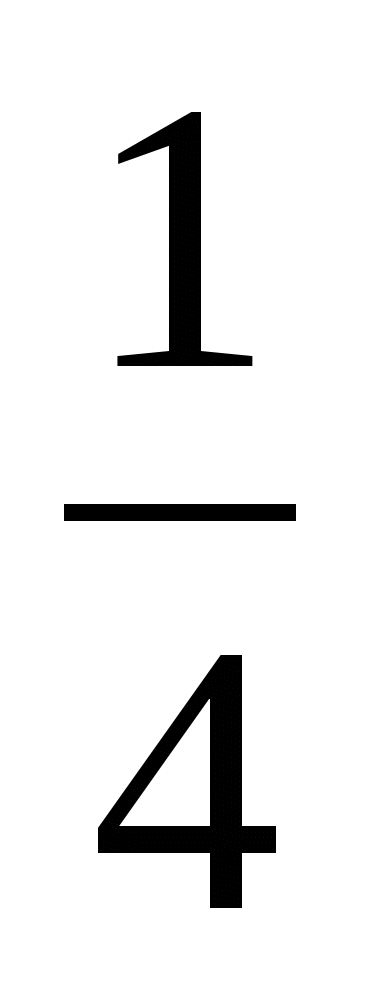
16. Центральный угол на 48 º больше вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный уголэ Ответ дайте в градусах.
17. Найдите центральный угол АОВ, если он 81 º больше вписанного угла АСВ, опирающегося на ту же дугу. Ответ дайте в градусах.
Задания В9: Геометрический смысл производной.
Теория: Геометрический смысл производной.
Производная функции в точке х равна угловому коэффиенту касательной (к):
Производная функции в точке х ровна тангенсу угла наклона касательной:
У параллельных прямых угловые коэффициенты равны (к) Например: у=3х+5 у=3х-1
Промежуток в котором производная положительна, то на этом промежутке функция ворастает.
Промежуток в котором производная отрицательна, то на этом промежутке функция убывает.
Чтобы найти наибольшее (наименьшее) значение функции, нужно сравнить значение функции в критических точках (это точки в которых производная равна 0 или не существует) и на концах данного отрезка.
Задание 1. Прямая 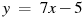
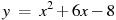
Решение: Найдем производную второй функции: у´= 2х + 6 2х + 6 = 7 х = 0,5
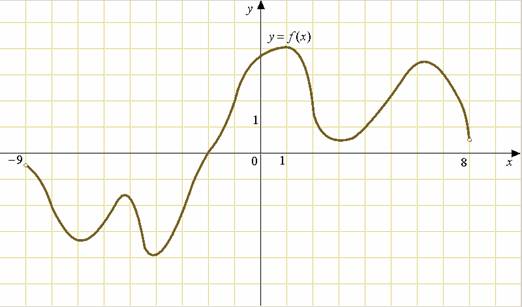
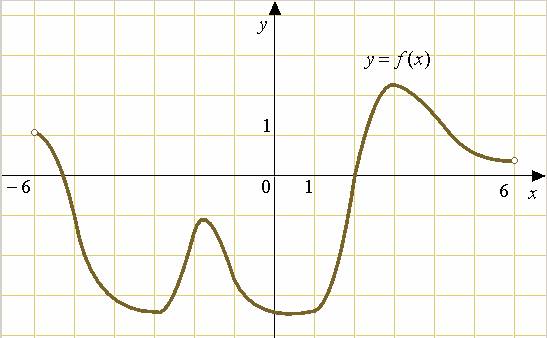
Задание 2. На рисунке изображен график функции 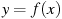
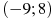
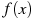
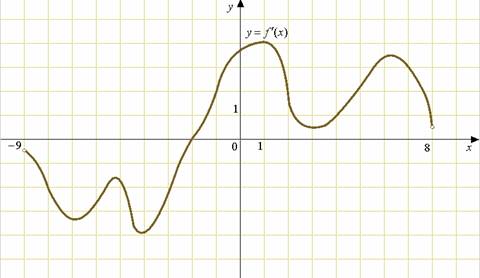
1. На рисунке изображен график производной функции 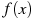
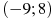
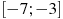
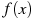
2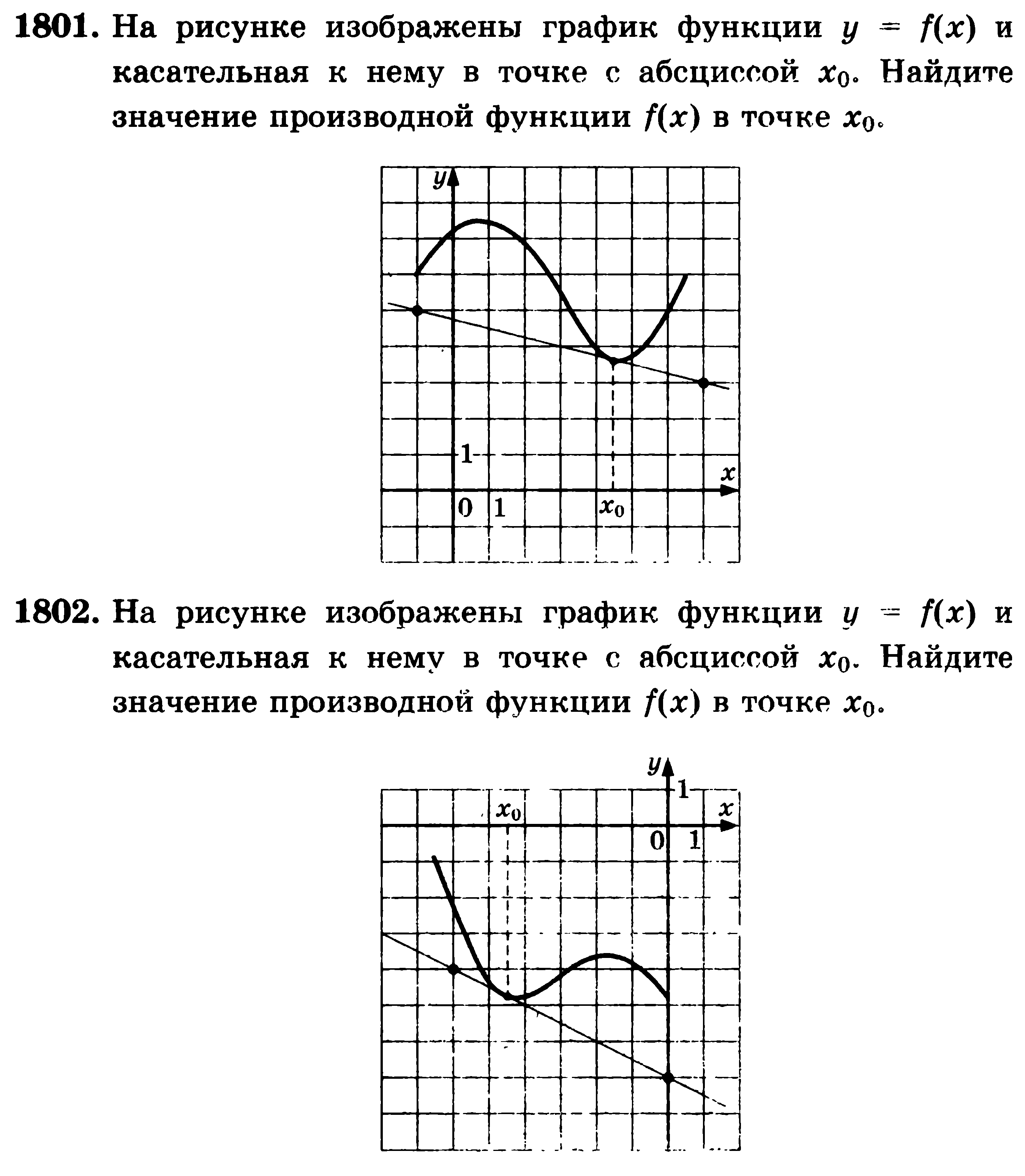
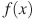
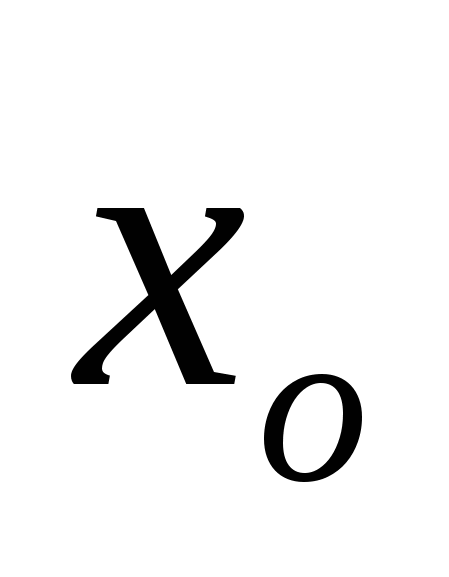
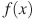
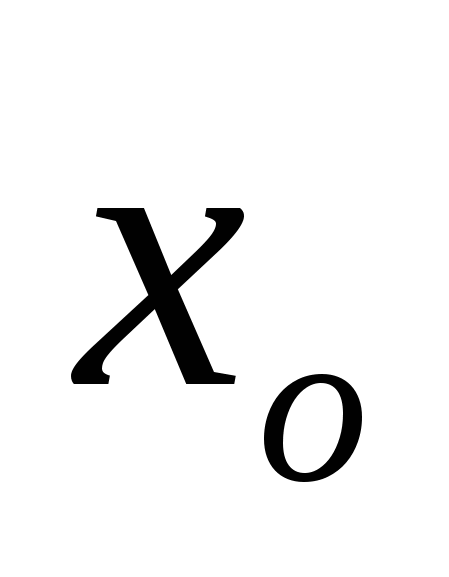
3.На рисунке изображены график функции у= 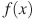
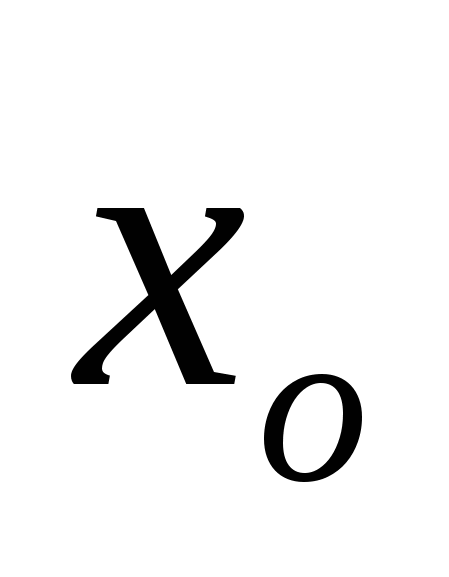
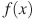
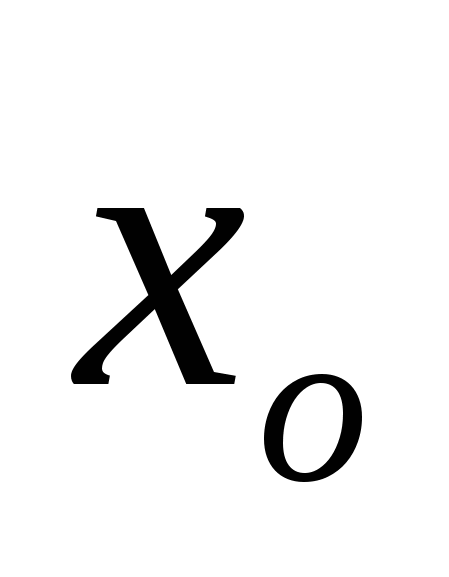
4. На рисунке изображен график производной функции 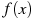
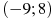
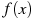
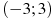
5. На рисунке изображен график функции 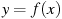
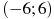
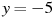
Задания В 10 Элементы стереометрии
Площадь основ ания
Пл ощадь бок ов поверхн ости
Полная поверхн ость
Формула площадей и объемов подобных фигур
Площади подобных фигур относятся как квадраты их соответствующих линейных размеров. Объемы подобных фигур относятся, как квадраты их соответствующих линейных размеров.
Задача1: Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника п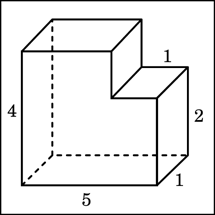
Решение: Объем параллелепипеда:
где a,b,c – линейные измерения прямоугольного параллелепипеда. Найдем объем вырезанного (маленького) параллелепипеда. Его стороны 1, 1, 2, значит объем равен: Vм = 1*1*2=2
Найдем объем большого параллелепипеда (если бы он был целым). Его стороны 5, 4, 1, значит объем равен: 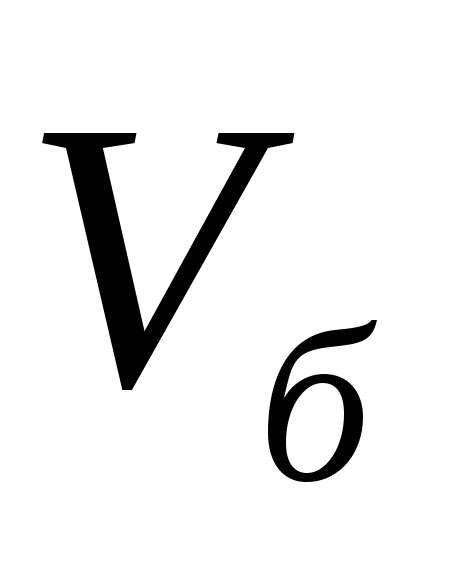
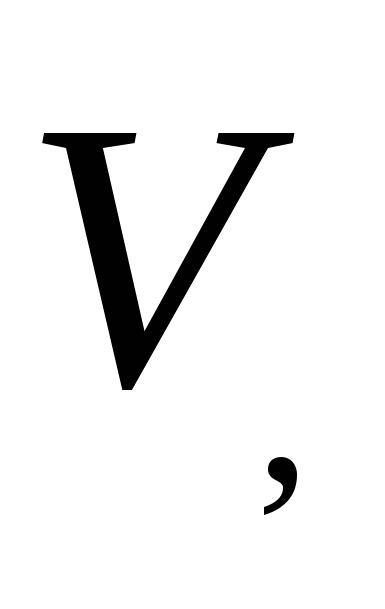
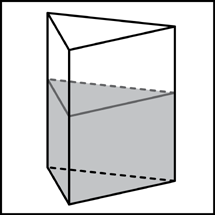
Задача2: В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первог
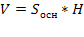
где Sосн – площадь основания призмы, а h-высота призмы.
Пусть сторона основания исходного сосуда a.
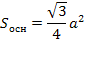
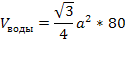
Пусть теперь сторона основания сосуда равна 4a. Найдем объем налитой воды.
Приравняем о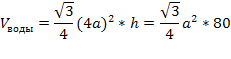
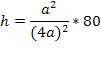
Задача3: В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SC=5, AC=6. Найдите длину отрезка SO.

1. О – точка пересечения диагоналей квадрата, то О D = 3.
2. Из прямоугольного треугольника S О D нужно найти SO по теореме Пифагора: 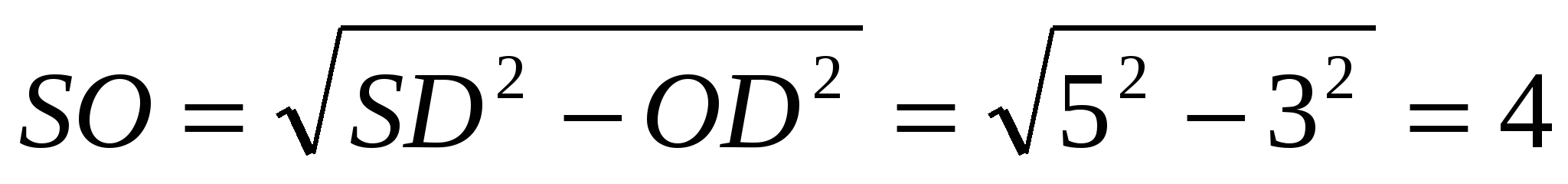
2. Площадь боковой поверхности цилиндра равна 2π, а диаметр основания — 1. Найдите высоту цилиндра.
10. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO=4, AC=6. Найдите боковое ребро SC
11. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SC=5, AC=6. Найдите длину отрезка SO.
12. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO=4, SC=5. Найдите длину отрезка AC.
13. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BD1=3, CD=2,AD=2. Найдите длину ребра AA1.
14. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что DD1=1, CD=2, AD=2. Найдите длину диагонали CA1.
16.Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
17.Во сколько раз уменьшится объем конуса, если его высота уменьшится в 3 раза, а радиус основания останется прежним?
18.Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
Задания В11 Вычисления выражений
Свойства логарифмов : 1.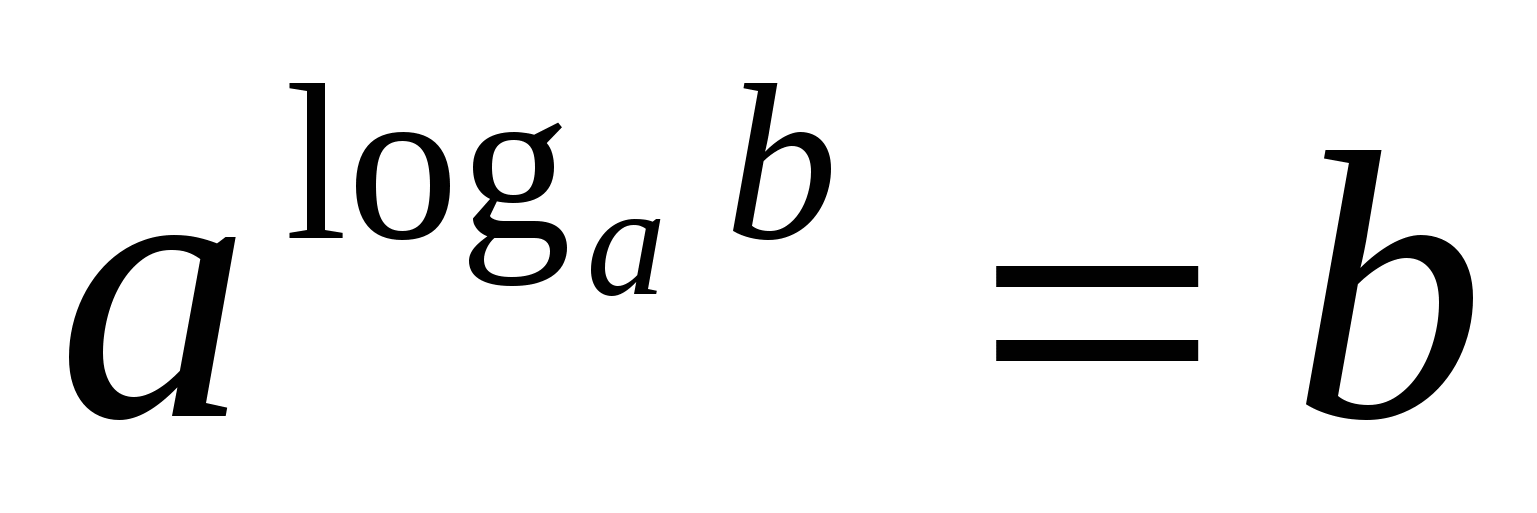
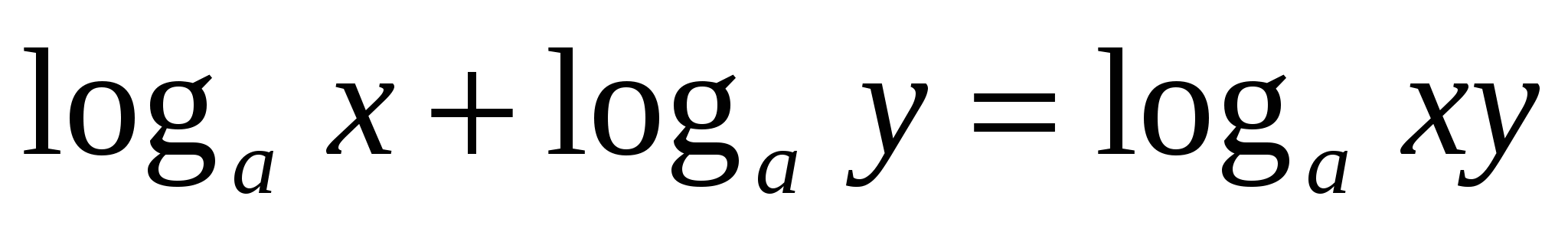
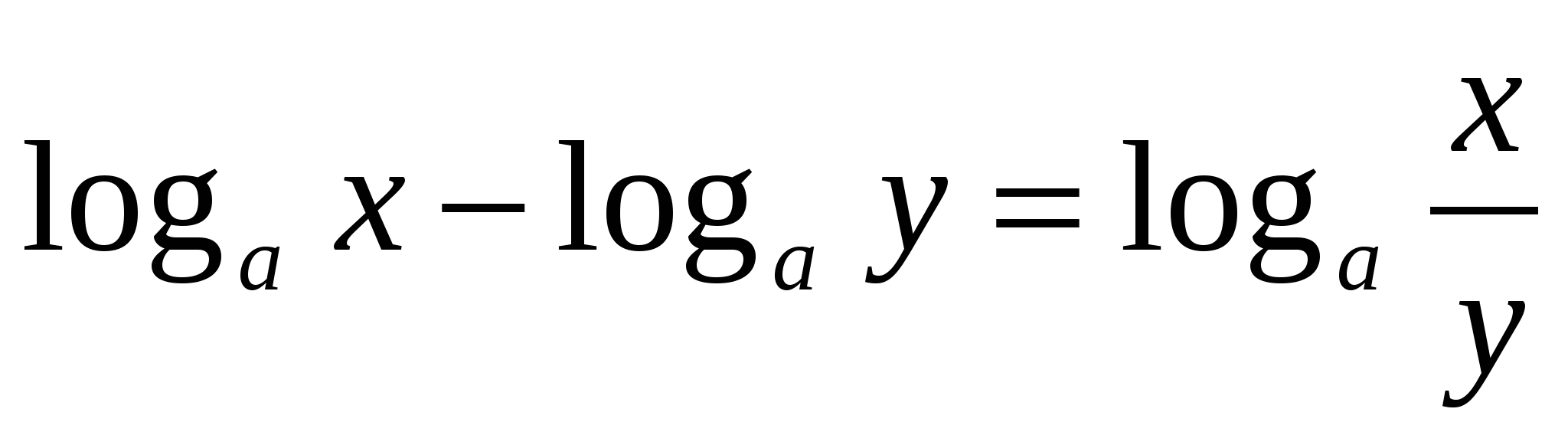
4. 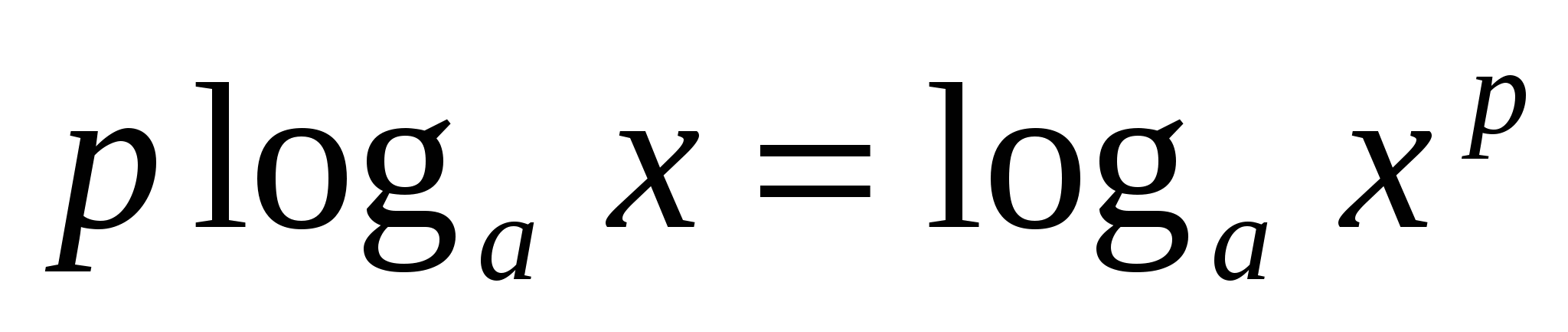
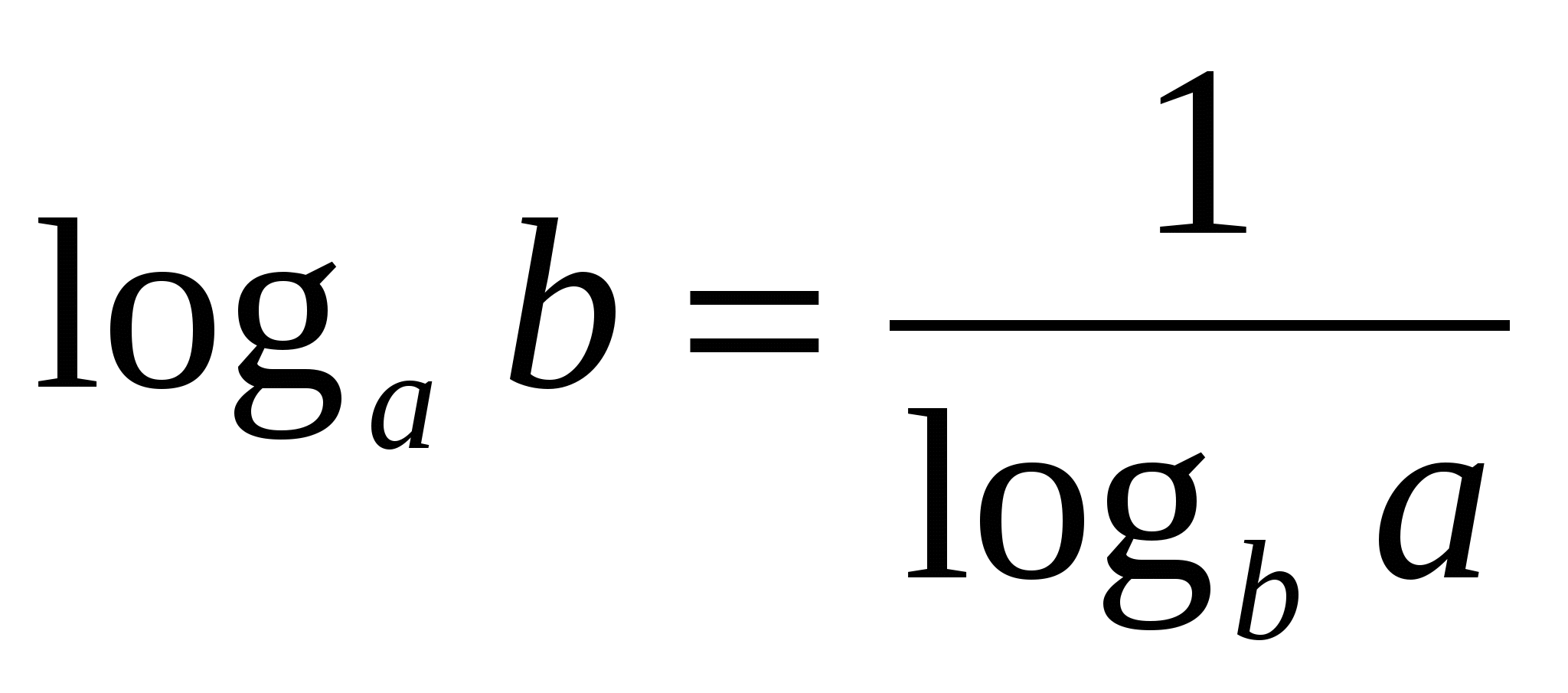
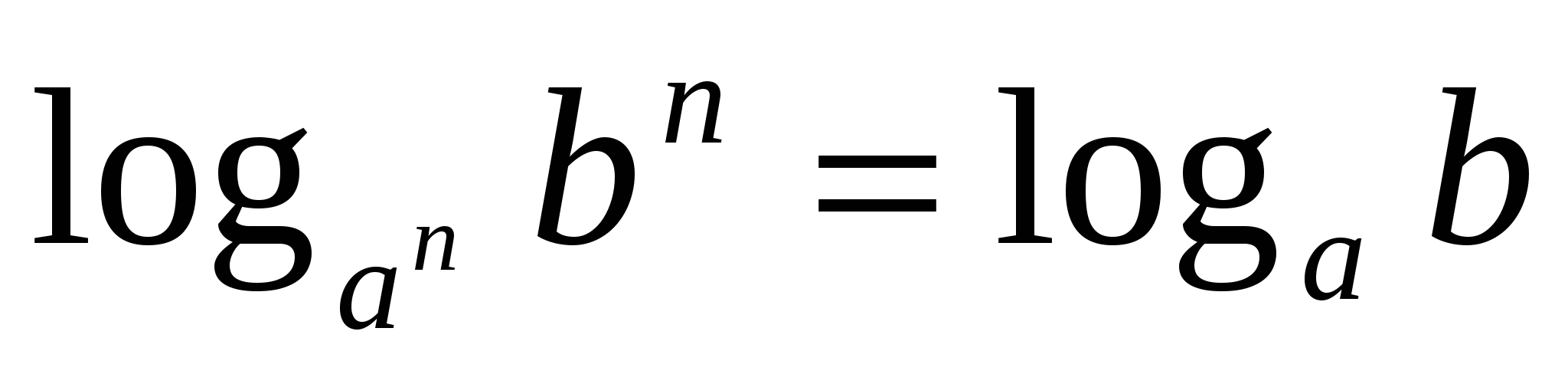
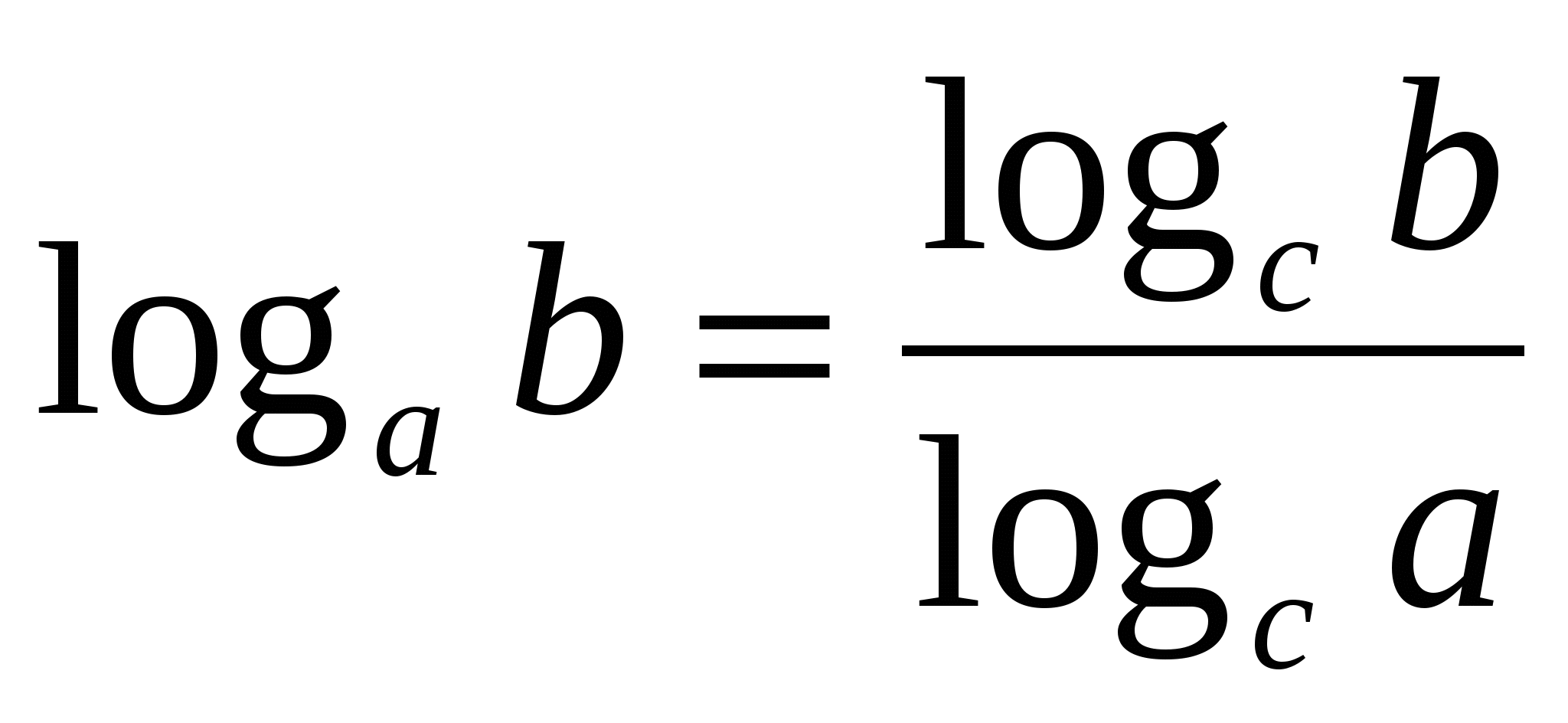
Теория 2: Степень: 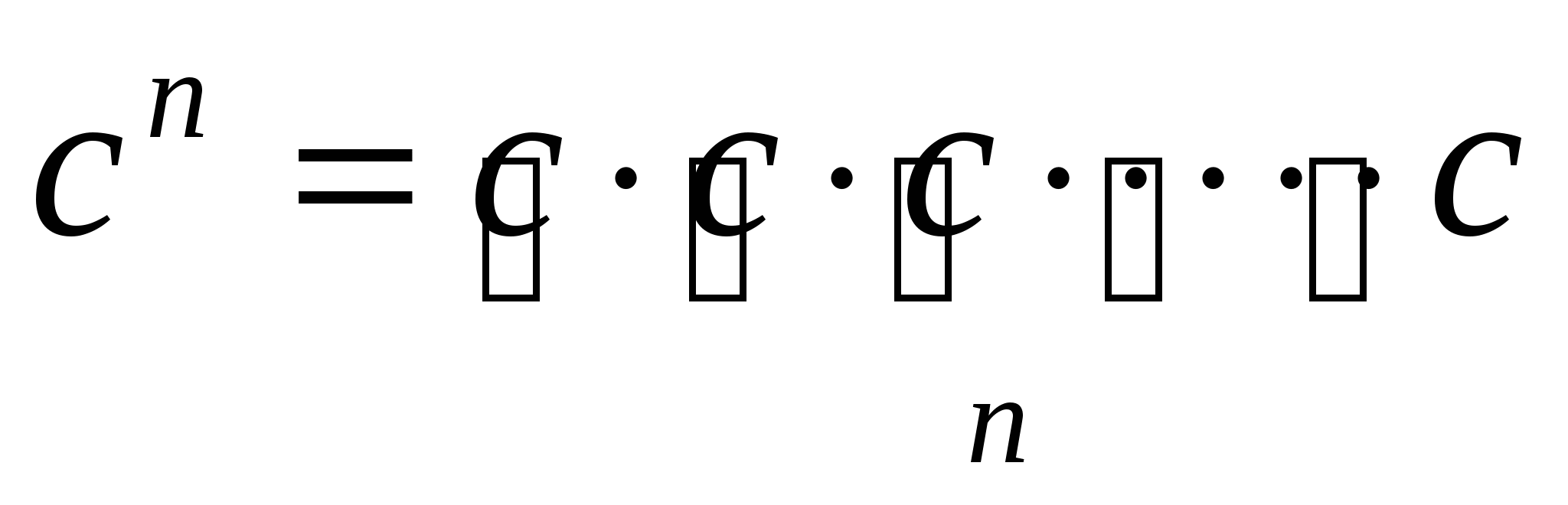

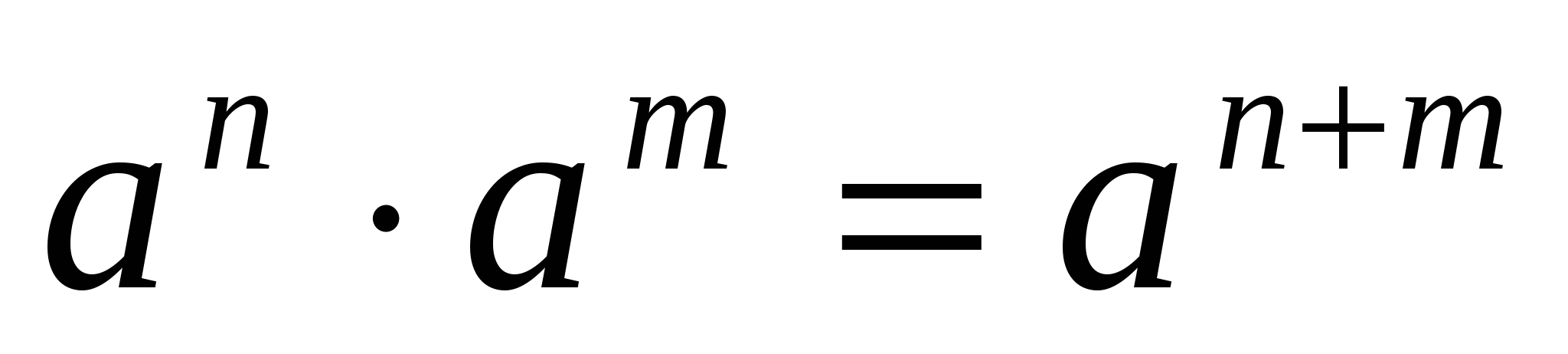
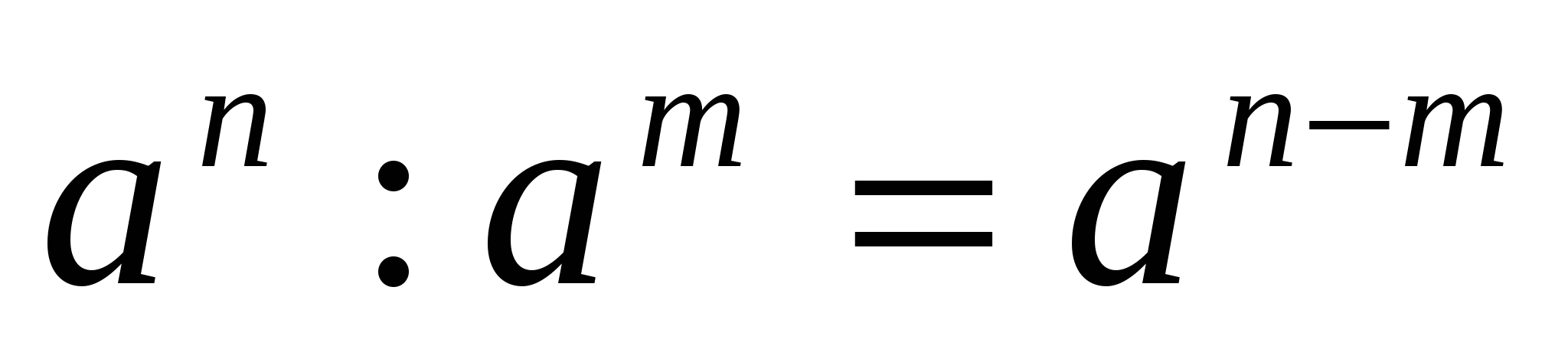
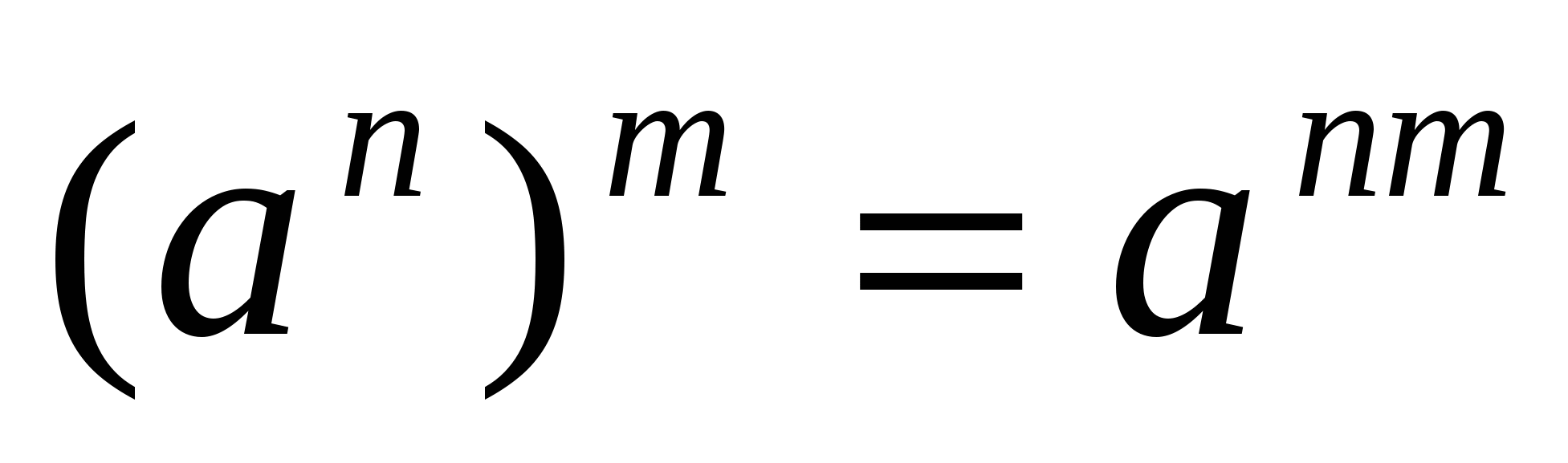
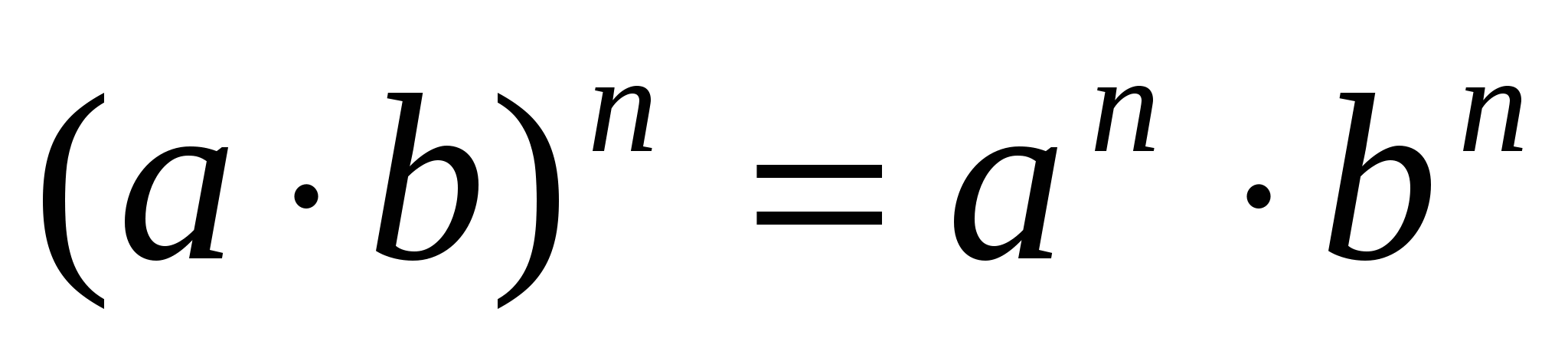
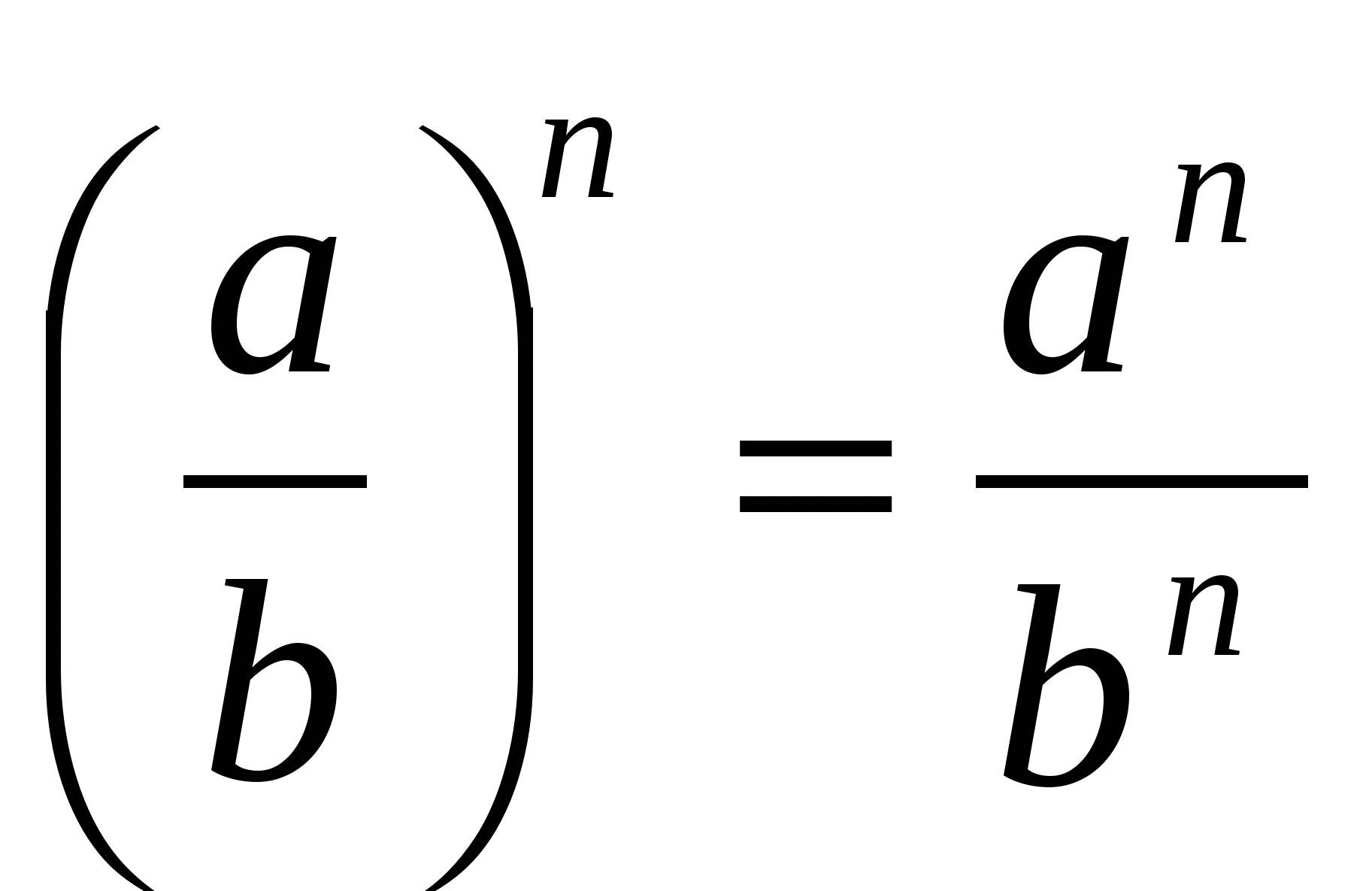
Тригон-ие тождества: 1. 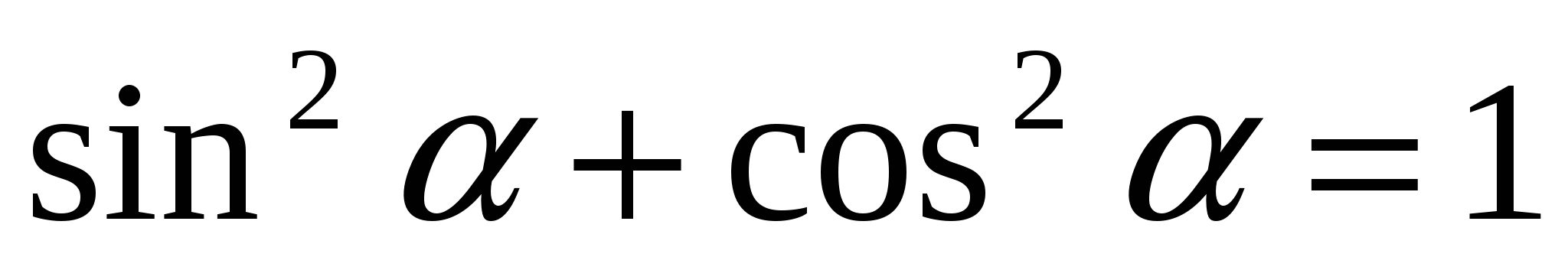
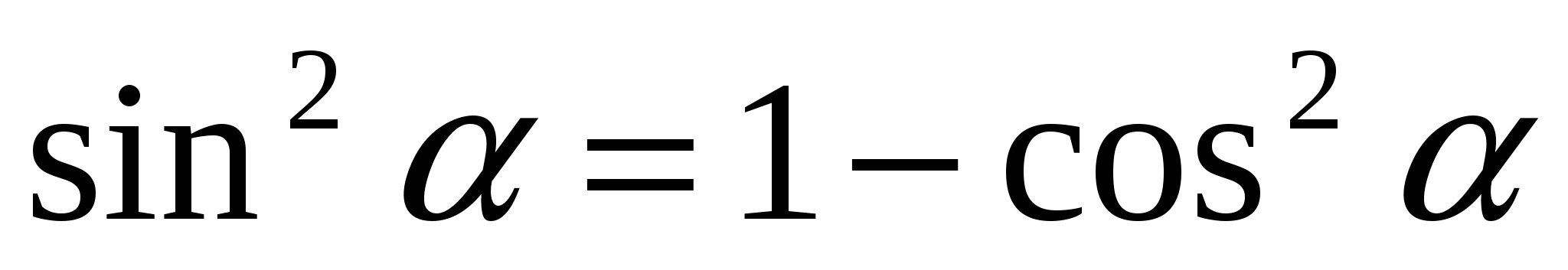
4. 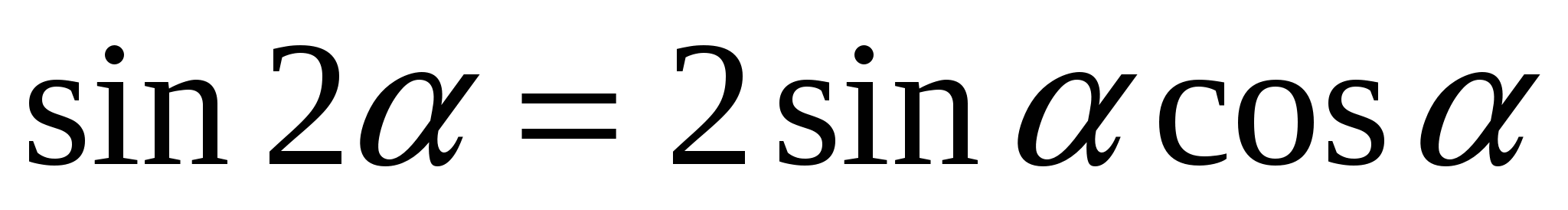
6. 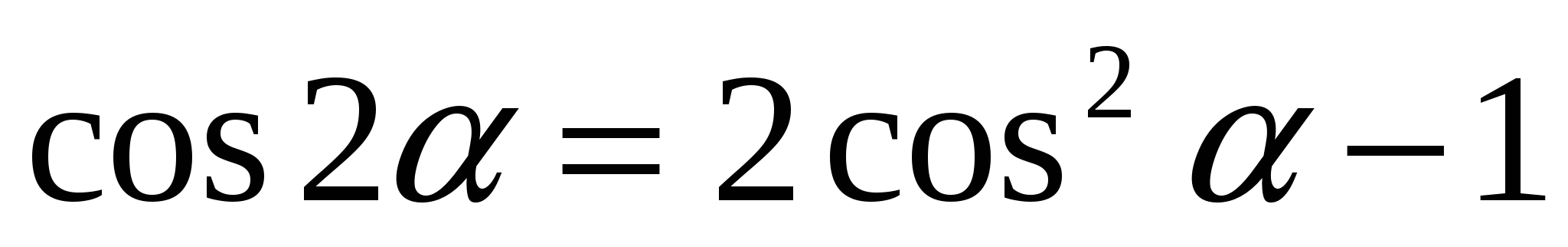
1. Найдите значение выражения 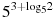
2. Найдите значение выражения 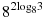
3. Найдите значение выражения 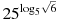
4. Найдите значение выражения 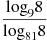
5. Найдите значение выражения 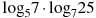
6. Найдите значение выражения
7. Найдите значение выражения
8. Найдите значение выражения 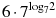
9. Найдите значение выражения
10. Найдите значение выражения 
11. Найдите значение выражения 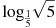
12. Найдите значение выражения 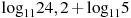
13. Найдите значение выражения 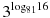
14. Найдите значение выражения
15.Найдите значение выражения
16. Найдите значение выражения
17. Найдите значение выражения
18. Найдите значение выражения
19. Найдите значение выражения
20. Найдите значение выражения
21.Найдите значение выражения
22. Найдите значение выражения
Задание B1 2 Задачи п рикладн ого содержания
Теория: Чтобы найти наибольше е или наименьше е значения нужно составить и решить по условию задачи линейное или квадратное неравенство.
1. Для одного из предприятий-монополистов зависимость объёма спроса на продукцию q (единиц в месяц) от её цены p (тыс. руб.) задаётся формулой: 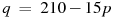
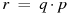
Решение: Подставим в значение выручки:
зависимость объёма спроса на продукцию q от её цены p:
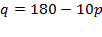
По условию задачи выручка больше 720 тыс. руб.
Корни квадратного уравнения: 12 и 6
1. Модель камнеметательной машины выстреливает камни под определенным углом к горизонту с фиксированной начальной скоростью. Её конструкция такова, что траектория полета камня описывается формулой 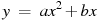
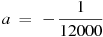
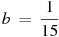
2. В боковой стенке цилиндрического бака вблизи дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём меняется по закону 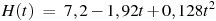
3. В боковой стенке цилиндрического бака вблизи дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём меняется по закону 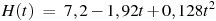
4. Зависимость температуры (в градусах Кельвина) от времени (в минутах) для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур задаётся выражением 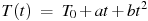
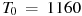
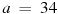
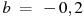
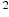
5. Коэффициент полезного действия некоторого двигателя определяется формулой 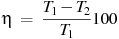

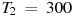
6. В розетку электросети подключены приборы, общее сопротивление которых составляет 100Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите (в омах) наименьшее возможное сопротивление электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями 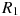
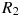
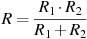
7. Для определения эффективной температуры звёзд используют закон Стефана — Больцмана, согласно которому мощность излучения нагретого тела вычисляется по формуле: 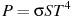
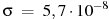
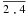
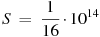
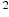
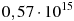
8. Модель камнеметательной машины, выстреливает камни под определенным углом к горизонту с фиксированной начальной скоростью. Её конструкция такова, что траектория полета камня описывается формулой 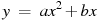
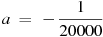
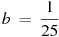
9. Если достаточно быстро вращать ведерко с водой на веревке в вертикальной плоскости, то вода не будет выливаться. При вращении ведерка сила давления воды на дно не остается постоянной: она максимальна в нижней точке и минимальна в верхней. Вода будет выливаться, если сила ее давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна