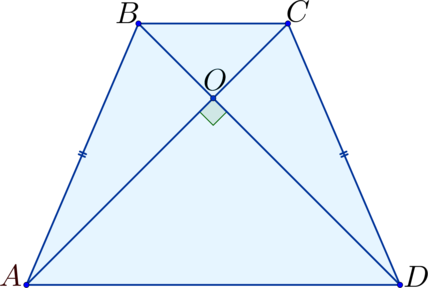
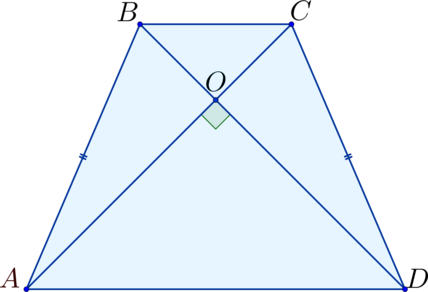
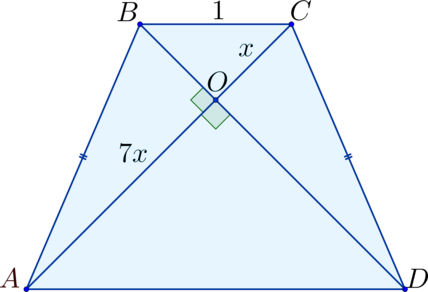
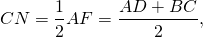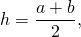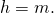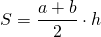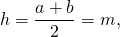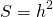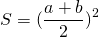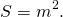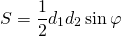В равнобокой трапеции диагонали перпендикулярны боковым сторонам чему равна площадь 36 60
Узнать ещё
Знание — сила. Познавательная информация
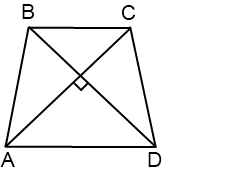
В равнобедренной трапеции диагонали перпендикулярны
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
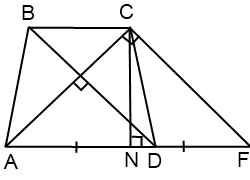
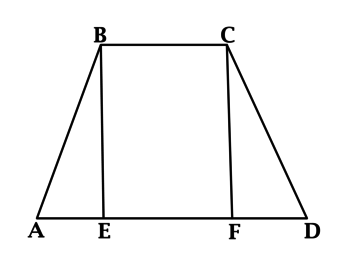
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
Четырехугольник BCFD — параллелограмм ( BC ∥ DF как основания трапеции, BD ∥ CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
что в общем виде можно записать как
где h — высота трапеции, a и b — ее основания.
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
sin 90 º =1, и диагонали равнобедренной трапеции равны, то площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна
Признаки и свойства равнобедренной трапеции
\(\blacktriangleright\) Равнобедренная трапеция – трапеция, у которой боковые стороны равны.
Свойства равнобедренной трапеции:
\(\blacktriangleright\) Углы при каждом основании равны;
\(\blacktriangleright\) Диагонали равны;
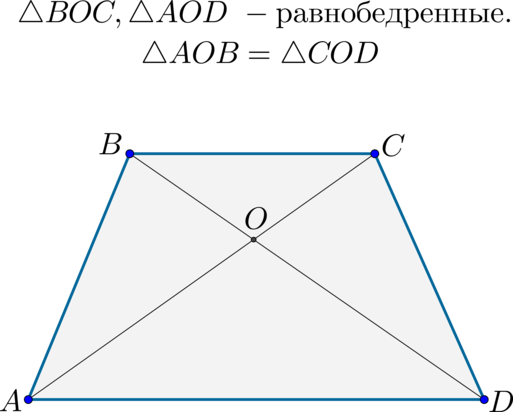
\(\blacktriangleright\) Два треугольника, образованные диагоналями и одним из оснований, являются равнобедренными;
\(\blacktriangleright\) Два треугольника, образованные диагоналями и боковой стороной, равны.
\[\begin
В равнобедренной трапеции \(ABCD\) основание \(AD\) вдвое длиннее основания \(BC\) и боковой стороны. Найдите острый угол трапеции.
Учащимся старших классов, которые готовятся сдавать ЕГЭ по математике, в обязательном порядке стоит повторить тему «Равнобедренная трапеция» и освежить в памяти ее основные свойства и признаки. Многолетняя практика показывает, что подобные задания ежегодно встречаются в программе аттестационного испытания. Поэтому, если вы хотите успешно решить задачи ЕГЭ на применение основных свойств диагоналей или углов равнобедренной трапеции, вам непременно стоит разобраться в этой теме.
Образовательный портал «Школково» предлагает новый подход к подготовке к аттестационному испытанию. Наш ресурс позволяет учащимся определить наиболее сложные темы и ликвидировать имеющиеся пробелы в знаниях. Специалисты «Школково» подготовили и изложили весь материал в максимально доступной форме.
Чтобы выпускники могли успешно справляться с геометрическими задачами, мы рекомендуем вспомнить определение равнобедренной трапеции, свойства ее сторон, углов и диагоналей, а также формулу для вычисления площади. Эта информация представлена в разделе «Теоретическая справка».
Вспомнив основные свойства углов, диагоналей и сторон равнобедренной трапеции, учащиеся имеют возможность закрепить усвоенный материал, выполнив практические задания. Упражнения различного уровня сложности представлены в разделе «Каталог». В каждом из них вы найдете подробный алгоритм решения и правильный ответ.
Практиковаться в выполнении заданий по теме «Трапеция» при подготовке к ЕГЭ выпускники могут в режиме онлайн, находясь не только в Москве, но и в любом другом городе России. В случае необходимости любое упражнение можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.
Высота равнобокой трапеции равна 10 см а ее диагонали перпендикулярны?
Высота равнобокой трапеции равна 10 см а ее диагонали перпендикулярны.
Найдите боковую сторону трапеции если ее периметр равен 48 см.
Если в равнобокой трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Значит, BE = ½ (BC + AD).
Следовательно, BC + AD = BE * 2.
AB = 28 см : 2 = 14 см.
AB = CD = 14см, так как трапеция равнобокая.
Найдите длину диагонали трапеции.
Основания равнобедренной трапеции равны 16 и 96, боковая сторона равна 58?
Основания равнобедренной трапеции равны 16 и 96, боковая сторона равна 58.
Найдите длину диагонали трапеции.
Основания равнобедренной трапеции равны 12 и 42, боковая сторона равна 39?
Основания равнобедренной трапеции равны 12 и 42, боковая сторона равна 39.
Найдите длину диагонали трапеции.
В равнобокой трапеции боковая сторона равна средней линии, а периметр = 40?
В равнобокой трапеции боковая сторона равна средней линии, а периметр = 40.
Найдите длину средней линии трапеции.
Диагональ равнобокой трапеции перпендикулярна боковой стороне и образует с основанием трапеции угол а?
Диагональ равнобокой трапеции перпендикулярна боковой стороне и образует с основанием трапеции угол а.
Найдите высоту трапеции, если радиус окружности, описанной около трапеции, равен h.
Периметр трапеции равен 60, а одна боковая сторона равна 5?
Периметр трапеции равен 60, а одна боковая сторона равна 5.
Найдите среднюю линию трапеции, если трапецию можно вписать в окружность.
Если в равнобокой трапеции острый угол равен 30, меньшее основание равно боковой стороне и равно 4 см, то площадь трапеции равна?
Если в равнобокой трапеции острый угол равен 30, меньшее основание равно боковой стороне и равно 4 см, то площадь трапеции равна?
Если периметр равнобокой трапеции равен 40, радиус вписанной в трапецию окружности равен 3 см, то площадь трапеции равна?
Если периметр равнобокой трапеции равен 40, радиус вписанной в трапецию окружности равен 3 см, то площадь трапеции равна?
Периметр равнобокой трапеции 18см?
Периметр равнобокой трапеции 18см.
Найдите боковую сторону трапеции.
Докажите что если в равнобокой трапеции высота равна средней линии то диагонали трапеции взаимно перпендикулярны?
Докажите что если в равнобокой трапеции высота равна средней линии то диагонали трапеции взаимно перпендикулярны.