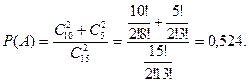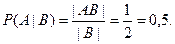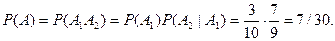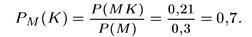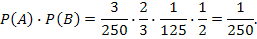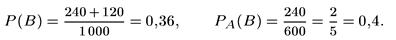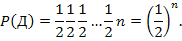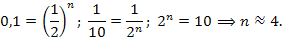В семье 2 детей какова вероятность что старший ребенок мальчик

Основные формулы теории вероятностей

Задача 1. В ящике 10 красных и 5 синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность, что пуговицы будут одноцветными?

Решение. Событие A= <вынуты пуговицы одного цвета>можно представить в виде суммы , где события и означают выбор пуговиц красного и синего цвета соответственно. Вероятность вытащить две красные пуговицы равна , а вероятность вытащить две синие пуговицы . Так как события и не могут произойти одновременно, то в силу теоремы сложения

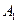
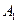
Задача 2. Среди сотрудников фирмы 28% знают английский язык, 30% – немецкий, 42% – французский; английский и немецкий – 8%, английский и французский – 10%, немецкий и французский – 5%, все три языка – 3%. Найти вероятность того, что случайно выбранный сотрудник фирмы: а) знает английский или немецкий; б) знает английский, немецкий или французский; в) не знает ни один из перечисленных языков.

Решение. Обозначим через A, B и С события, заключающиеся в том, что случайно выбранный сотрудник фирмы владеет английским, немецким или французским соответственно. Очевидно, доли сотрудников фирмы, владеющих теми или иными языками, определяют вероятности этих событий. Получаем:

Задача 3.В семье – двое детей. Какова вероятность, что старший ребенок – мальчик, если известно, что в семье есть дети обоего пола?

Решение. Пусть А=<старший ребенок – мальчик>, B=<в семье есть дети обоего пола>. Будем считать, что рождение мальчика и рождение девочки – равновероятные события. Если рождение мальчика обозначить буквой М, а рождение девочки – Д, то пространство всех элементарных исходов состоит из четырех пар: 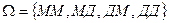. В этом пространстве лишь два исхода (МД и ДМ) отвечают событию B. Событие AB означает, что в семье есть дети обоего пола. Старший ребенок – мальчик, следовательно, второй (младший) ребенок – девочка. Этому событию AB отвечает один исход – МД. Таким образом, |AB|=1, |B|=2 и

Задача 4. Мастер, имея 10 деталей, из которых 3 – нестандартных, проверяет детали одну за другой, пока ему не попадется стандартная. Какова вероятность, что он проверит ровно две детали?

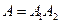
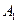
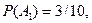
Решение. Событие А= <мастер проверил ровно две детали>означает, что при такой проверке первая деталь оказалась нестандартной, а вторая – стандартная. Значит, , где = < первая деталь оказалась нестандартной >и =<вторая деталь – стандартная>. Очевидно, что вероятность события А₁ равна кроме того, , так как перед взятием второй детали у мастера осталось 9 деталей, из которых только 2 нестандартные и 7 стандартных. По теореме умножения

Задача 5.В одном ящике 3 белых и 5 черных шаров, в другом ящике – 6 белых и 4 черных шара. Найти вероятность того, что хотя бы из одного ящика будет вынут белый шар, если из каждого ящика вынуто по одному шару.

Решение. Событие A= <хотя бы из одного ящика вынут белый шар>можно представить в виде суммы , где события и означают появление белого шара из первого и второго ящика соответственно. Вероятность вытащить белый шар из первого ящика равна , а вероятность вытащить белый шар из второго ящика . Кроме того, в силу независимости и имеем: . По теореме сложения получаем: .

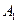
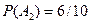
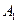
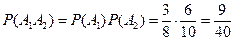
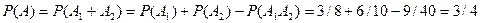
Задача 6. Три экзаменатора принимают экзамен по некоторому предмету у группы в 30 человек, причем первый опрашивает 6 студентов, второй — 3 студентов, а третий — 21 студента (выбор студентов производится случайным образом из списка). Отношение трех экзаменаторов к слабо подготовившимся различное: шансы таких студентов сдать экзамен у первого преподавателя равны 40%, у второго — только 10%, у третьего — 70%. Найти вероятность того, что слабо подготовившийся студент сдаст экзамен.

Решение. Обозначим через гипотезы, состоящие в том, что слабо подготовившийся студент отвечал первому, второму и третьему экзаменатору соответственно. По условию задачи

, , .

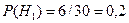
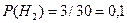
Пусть событие A=<слабо подготовившийся студент сдал экзамен>. Тогда снова в силу условия задачи

, , .

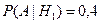
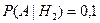
По формуле полной вероятности получаем:

.

Задача 7. Фирма имеет три источника поставки комплектующих – фирмы А, B, С. На долю фирмы А приходится 50% общего объема поставок, В – 30% и С – 20%. Из практики известно, что среди поставляемых фирмой А деталей 10% бракованных, фирмой В – 5% и фирмой С – 6%. Какова вероятность, что взятая наугад деталь окажется годной?

Решение. Пусть событие G – появление годной детали. Вероятности гипотез о том, что деталь поставлена фирмами А, B, С, равны сответственно Р(А)=0,5, Р(В)=0,3, Р(С)=0,2. Условные вероятности появления при этом годной детали равны Р(G|A)=0,9, P(G|B)=0,95, P(G|C)=0,94 (как вероятности противоположных событий к появлению бракованной). По формуле полной вероятности получаем:

Задача 8 (см. задачу 6). Пусть известно, что студент не сдал экзамен, т.е. получил оценку «неудовлетворительно». Кому из трех преподавателей вероятнее всего он отвечал?

Решение. Вероятность получить «неуд» равна . Требуется вычислить условные вероятности. По формулам Байеса получаем:

, и аналогично,

, .

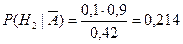
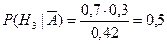
Отсюда следует, что, вероятнее всего, слабо подготовившийся студент сдавал экзамен третьему экзаменатору.

Дата добавления: 2015-01-29 ; просмотров: 316 ; Нарушение авторских прав

Источник

Теория Вероятности: две простые и интересные задачи

Как утверждал Цицерон: «Вероятностные знания — вот предел человеческого разумения». Действительно, как показывает мой опыт именно с этим разделом математики связаны наибольшие затруднения у студентов, да и не только, даже у отцов основателей этой науки нередко возникали проблемы с пониманием некоторых моментов.
Рассмотрим две задачи, для начало попробуйте решить их самостоятельно, ниже я приведу решение и пояснения к ним.

Задача 1.
Какова вероятность того, что в семье из двух детей оба ребенка будут мальчиками?

Задача 2.
В семье из двух детей младший ребенок мальчик, какова вероятность того, что старший тоже мальчик?

Давай те рассмотрим решения данных задач, но для начала вспомним элементарное определение вероятности.

Вероятностью наступления события А называется отношение n — числа благоприятных исходов, к m — общему числу исходов.

Каково множество всех исходов для первой задачи?
1 – M M
2 – М Д
3 – Д М
4 – Д Д
m=4

Каково множество благоприятных исходов?
1 – М М
n=1
Нетрудно видеть, что ответ для первой задачи будет P(A)=n/m =1/4

Для второй задачи множество исходов будет составлять:
1 – Д М
2 – М М
m=2

Множество благоприятных событий всего одно М и М. Итого: ответ для второй задачи будет P(b)=n/m=1/2

Резюме.
Задачи, казалось бы, имеют очень схожий смысл, но необходимо внимательно относиться к условиям. Подобного типа задачи вызывают «ужас» у многих людей тем, что после оглашения результатов складывается ощущение, что в них был заложен подвох. Хочу закончить простыми советами:

1) Пытайтесь дробить задачу на простые части, в данном случае это определение множеств (благоприятных и всех).
2) Перепроверяйте себя, ответ который пришел в вашу голову за первые секунды скорее всего не верный.
3) Верьте в себя.

Источник

Условная вероятность, закон умножения вероятностей

Условная вероятность события В – это вероятность события В, найденная при условии, что событие А произошло. Обозначается Р(В|А).

В коробке содержится 3 белых и 3 желтых таблетки. Из коробки дважды вынимают наугад по одной таблетке, не возвращая их в коробку. Найти вероятность появления белых таблеток при втором испытании (событие В), если при первом испытании была извлечена желтая таблетка (событие А).

Решение: После первого испытания в коробке осталось 5 таблеток, из них 3 белых. Искомое условие вероятности: Р(В/А) = 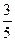= 0,6.

В коробке находится 8 красных и 6 белых таблеток. Из коробки последовательно без возвращения извлекают 3 таблетки. Найти вероятность того, что все 3 таблетки белые.

Обозначим; А₁ – первая таблетка белая, А₂ – вторая таблетка белая, А₃ – третья таблетка белая.

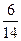
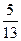
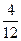
Р(A₁A₂A₃)=P(A₁)P(A₂/A₁) P(A₃/A₁A₂);

P(A₁)= ; P(A₂/A₁)= ; P(A₃/A₁A₂)= ;

P(A) = P(A₁A₂A₃)= .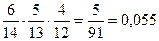

Произведение двух событий – это событие, состоящее в совместном появлении этих событий А и В.

Событие В называются независимым от события А, если появление события А не изменяет вероятности появления события В.

Вероятность появления нескольких независимых событий равна произведению вероятностей этих событий:

Р(А В)=Р(А) Р(В).

Для зависимых событий:

Р(АВ)=Р(А) Р(В/А).

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло.

Вероятность того, что у взрослого пациента все зубы сохранились равна 0,67. Какова вероятность того, что у двух не имеющих отношения друг к другу больных, ожидающих приема в кабинете стоматолога, есть все зубы?

Решение: Р(А В) = Р(А) Р(В) = 0,67 0,67 = 0,45.

В терапевтическом отделении больницы 70 % пациентов — женщины, а 21 % — курящие мужчины. Наугад выбирают пациента. Он оказывается мужчиной. Какова вероятность, что он курит?

Решение: Пусть М означает, что пациент — мужчина, а К — что пациент курит. Тогда в силу условия задачи Р(М) = 0,3, а Р(МК) = 0,21. Поэтому условная вероятность

Р(ММ) = Р(М) 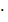Р(М) = 0,515 0,515 = 0,265;

Р(ДД) = 0,485 0,485 = 0,235;

Р(МД) = 0,515 0,485 = 0,25.

Решение: Вероятность иметь дизиготных близнецов равна:

P(A)= ;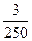

1–P(B)= .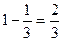

Вероятность того, что студент в летнюю сессию сдаст первый экзамен, равна 0,9; второй – 0,9; третий – 0,8. Найти вероятность того, что студентом будут сданы: 1) только второй экзамен; 2) все три экзамена.

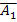
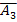
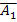
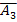
Решение: l) P(B) = P( A₂ ) = P( ) P(A₂) P( ) = 0,1 0,9 0,2 = 0,018;

2) Р(A₁A₂A₃)=P(A₁) P(A₂) P(A₃) = 0,9 0,9 0,8 = 0,648.

В группе обследуемых 1000 человек. Из них 600 курящих и 400 некурящих. Среди курящих 240 человек имеют те или иные заболевания легких. Среди некурящих легочных больных 120 человек. Являются ли курение и заболевание легких независимыми событиями?

Решение. Пусть событие А – обследуемый курит, событие В – обследуемый страдает заболеванием легких.

Тогда согласно условию задачи

Так как 0,36 ≠ 0,4, события А и В зависимы.

Вероятность выживания одного организма в течение 20 минут Р = 0,7. В пробирке с благоприятными для существования этих организмов условиями находятся только что родившиеся 2 организма. Какова вероятность того, что через 20 минут они будут живы?

Решение. Пусть событие А — первый организм жив через 20 мин, событие В — второй организм жив через 20 мин. Будем считать, что между организмами нет внутривидовой конкуренции, т. е. события А и В независимы. Событие, что оба организма живы, есть событие АВ. Получаем:

Решение: Вероятность того, что в мишень попадет первый стрелок и не попадет второй, равна:

P(A₁ 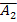) = 0,7 (1 – 0,8) = 0,7 0,2 = 0,14.

Вероятность того, что попадет второй стрелок в мишень и не попадет первый, равна:

P( 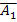A₂ ) = (1 – 0,7) 0,8 = 0,3 0,8 = 0,24.

Вероятность того, что в мишень попадет только один стрелок, равна сумме этих вероятностей:

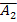
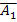
P(A₁ ) + P( A₂ ) = 0,14 + 0,24 = 0,38.

Сколько должна планировать пара иметь детей, чтобы вероятность хотя бы одного мальчика была выше 90% (вероятность рождения мальчика и девочки 0,5).

Решение: Пусть вероятность того, что все девочки:

Вероятность того, что не все девочки:

P(хотя бы один мальчик) = .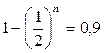

Варианты заданий

№ 12.1. В одном аквариуме находятся: 3 белые, 3 красные и 3 голубые рыбки. Трех случайно выбранных рыбок переносят в другой аквариум. Какова вероятность того, что все 3 рыбки белые?

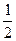
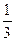
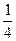
№ 12.2. Студент изучает биологию, химию и физику. Он оценивает, что вероятность получить «пятерку» по этим предметам равна соответственно: Р(Б) = ; Р(X) = ; Р(Ф) = . Предположим, что оценки студента по трем предметам независимы. Какова вероятность, что он: 1) Не получит ни одной «пятерки»? 2) Получит «пятерку» только по биологии?

№ 12.4. На лекции по биофизике во втором семестре присутствуют 124 студента. Из них на экзамене по высшей математике в зимнюю сессию получили оценку «отлично» 19 человек, «хорошо» – 50 человек, «удовлетворительно» – 24 и не сдали экзамен 31 человек. Какова вероятность того, что вызванные наугад один за другим два студента из числа присутствующих на лекции не имеют задолженности по высшей математике?

№ 12.5. Студент пришел на зачет, зная из 30 вопросов только 24. Какова вероятность сдать зачет, если после отказа отвечать на вопрос преподаватель задает еще один вопрос?

№ 12.6. Вероятность того, что в течение одного рабочего дня возникнет неполадка в определенном медицинском приборе равна 0,05. Какова вероятность того, что не произойдет ни одной неполадки за 3 рабочих дня?

№ 12.8. В коробке содержится 3 белых и 3 желтых таблетки. Из коробки дважды вынимают наудачу по одной таблетке, не возвращая в коробку. Найти вероятность появления белой таблетки при втором испытании (событие В), если при первом испытании была извлечена желтая таблетка (событие A).

№ 12.9. В коробке содержится 8 красных и 6 белых таблеток. Из коробки последовательно без возвращения извлекаются 3 таблетки. Найти вероятность того, что все таблетки белые.

№ 12.12. Отдел технического контроля проверяет медицинское изделие на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартное.

№ 12.13. Какова вероятность того, что у девочки, о которой известно, что она растет в семье, где четыре ребенка, есть старший брат?

№ 12.14. а) Сколько должна планировать супружеская пара иметь детей, чтобы вероятность хотя бы одного мальчика была выше 90%?

б) Сколько должна планировать супружеская пара иметь детей, чтобы вероятность хотя бы одного мальчика и одной девочки была выше 70%?

№ 12.15. а) Найдите вероятность того, что в семье из шестерых детей три мальчика и три девочки.

б) Найдите вероятность того, что в семье из шестерых детей все дети одного и того же пола.

№ 12.16. Представим, что в одной семье есть восемь детей — четыре мальчика и четыре девочки. Какова вероятность того, что старший ребенок – мальчик? Какова вероятность того, что все четыре мальчика старше четырех девочек?

№ 12.17. У пары три ребенка. Определим события А (первый ребенок – девочка), В (второй ребенок – мальчик), С (третий ребенок – мальчик), D (первые два ребенка – мальчики) и Е (хотя бы один ребенок –мальчик).

а) Вычислите вероятности этих пяти событий.

б) Являются ли независимыми А и D; А и Е; В и E?

в) Являются ли независимыми события В, С и E?

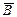
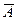
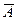
№ 12.18. Некоторая вакцина эффективна на 75% в формировании иммунитета. Вакцинировалось два человека. Пусть А и В — события, состоящие в том, что соответственно первый и второй человек приобретает иммунитет. Являются ли независимыми А и В; А и ; и В; и ? Найти вероятности этих пар событий.

№ 12.19. Три врача независимо друг от друга осмотрели одного и того же больного. Вероятность того, что 1-ый врач допустит ошибку при установлении диагноза, равна 0,01. Для 2-го и 3-го – 0,015 0,02 соответственно. Найти вероятность того, что хотя бы один из врачей допустит ошибку в диагнозе.

№ 12.20. Три крысы обучаются выполнению трех различных заданий (по одной крысе на каждое задание). Вероятности того, что крысы выполняют свои задания за 1 мин, составляют соответственно 2/3, 1/2 и 1/3. Какова вероятность того, что все три крысы выполнят свои задания за 1 мин? Что выполнят только две? Что выполнят хотя бы две?

№ 12.21. В одном городе вероятность грозы в любой данный день в течение августа составляет 0,25, а вероятность града — 0,1. Вероятность града во время грозы равна 0,3.

а) Являются ли независимыми события «град» и «гроза»?

б) Какова вероятность града в такой день, когда нет грозы?

№ 12.22. На трех фермах A, В и С произошла вспышка заболевания ящуром. Доля зараженного скота составляют соответственно 1/6, 1/4 и 1/3. Из каждой фермы случайным образом выбирают по одной корове.

а) Какова вероятность того, что заболевание имеется только у одной коровы?

б) Если заражена только одна корова, то какова вероятность, что эта корова выбрана из фермы A?

№ 12.23. Медицинский прибор проходит 3 стадии обработки. Вероятность получения брака на первой стадии равна 0,02; на второй – 0,03; на третьей – 0,02. Найдите вероятность получения прибора без брака после 3 стадий, предполагая, что получения брака на отдельных стадиях являются независимыми событиями.

№ 12.24. Студент успел подготовить к экзаменам 20 вопросов из 25. Какова вероятность того, что из 3 наудачу выбранных вопросов студент знает не менее 2?

№ 12.25. Студент разыскивает нужную ему формулу в трех справочниках. Вероятность того, что формула содержится в первом, втором и третьем справочниках, равна соответственно 0,6, 0,7 и 0,8. Найти вероятность того, что эта формула содержится не менее чем в двух справочниках.

Источник