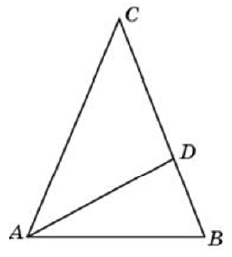
В треугольнике abc проведена биссектриса ad найдите bd если известно что

Решение №1966 В треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найдите меньший угол треугольника ABC.

В треугольнике 𝐴𝐵𝐶 проведена биссектриса 𝐴𝐷 и 𝐴𝐵 = 𝐴𝐷 = 𝐶𝐷. Найдите меньший угол треугольника 𝐴𝐵𝐶. Ответ дайте в градусах.

∠САD = ∠DCA = α

AD = АВ, тогда ΔAВD равнобедренный, углы при основании равны, сумма углов 180°, ∠ВАD = α, найдём ∠В :

Весь угол А равен:

∠А = α + α = 2α

Все три угла треугольника АВС обозначили, зная что сумма равна 180º, составим уравнение:

Найдём другие два угла:

Наименьший угол равен 36º.

Источник

В треугольнике abc проведена биссектриса ad найдите bd если известно что

В треугольнике ABC проведены BK — медиана, BE — биссектриса, AD — высота. Известно, что прямые BK и BE делят отрезок AD на три равные части.

а) Докажите, что треугольник ABC — тупоугольный.

б) Найти длину стороны AC, если AB = 4.

а) Пусть треугольник ABC не является тупоугольным. Тогда его высота AD лежит внутри треугольника или совпадает с его стороной. Тогда BD ⩽ AB. Пусть прямая BE пересекает AD в точке F, прямая BK пересекает AD в точке G. По свойству биссектрисы Тогда Применим к треугольнику ACD и секущей BG теорему Менелая: откуда что невозможно. Получаем противоречие, значит, треугольник ABC тупоугольный.

б) По свойству биссектрисы откуда BD = 2, поэтому угол ABC = 60°. Применим к треугольнику ACD и секущей BG теорему Менелая:

Осталось применить для треугольника ABC теорему косинусов:

Ответ: б)

Источник

Рациональные методы решения задач повышенной сложности. Биссектрисы и медианы треугольника

В данной презентации рассматриваются малоизвестные свойства биссектрисы и медианы треугольника, на примере задач ОГЭ и ЕГЭ показано их применение.

Содержимое разработки

Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.

Рациональные методы решения задач повышенной сложности. Биссектрисы и медианы треугольника

Что мы знаем о биссектрисе треугольника из школьного учебника?

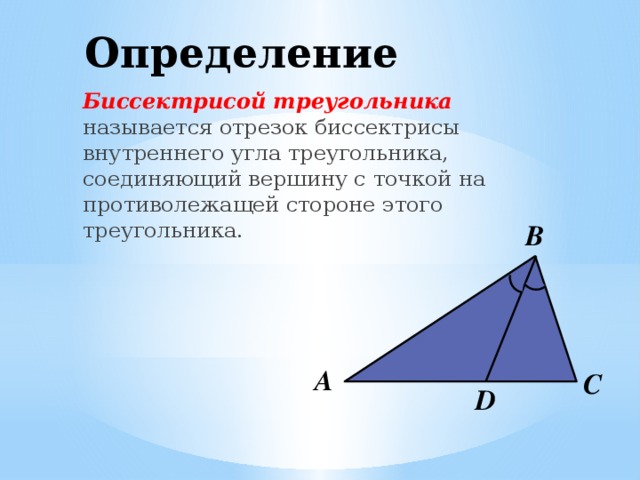
Биссектрисой треугольника называется отрезок биссектрисы внутреннего угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.

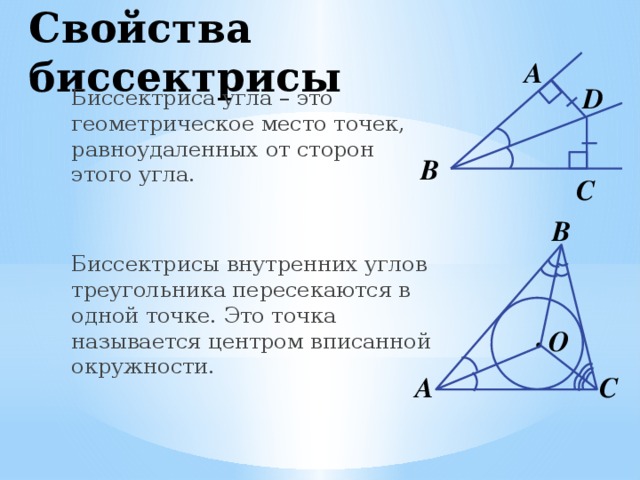
Биссектриса угла – это геометрическое место точек, равноудаленных от сторон этого угла.

Биссектрисы внутренних углов треугольника пересекаются в одной точке. Это точка называется центром вписанной окружности.

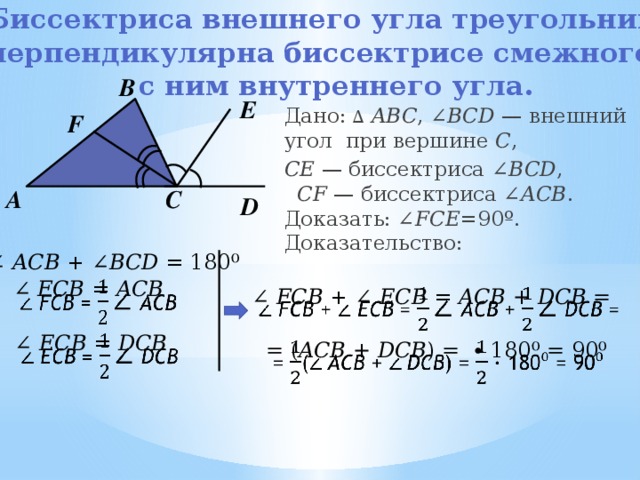
Биссектриса внешнего угла треугольника

перпендикулярна биссектрисе смежного

с ним внутреннего угла.

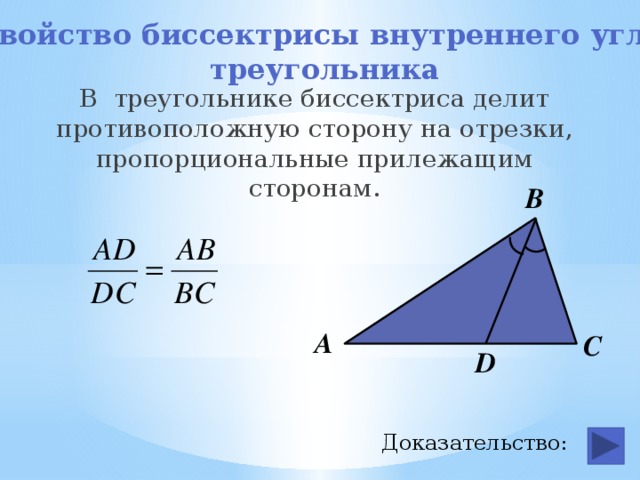
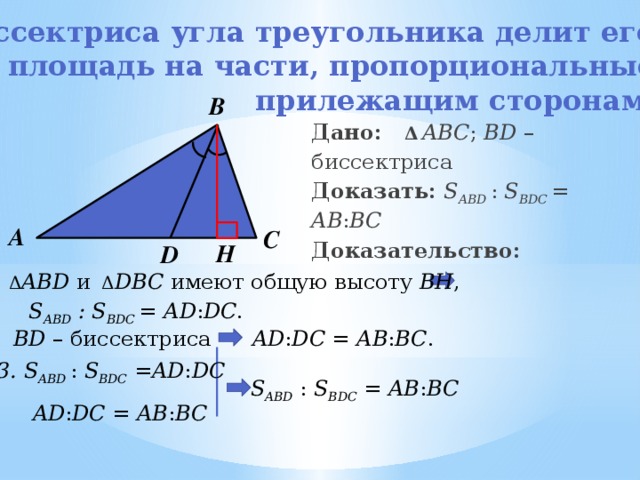
Свойство биссектрисы внутреннего угла

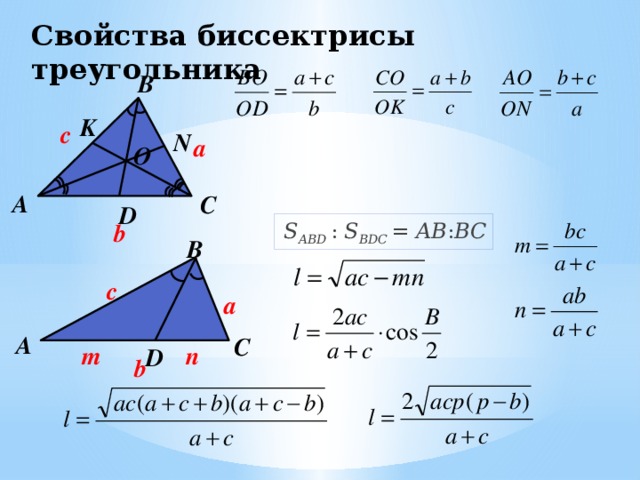
В треугольнике биссектриса делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.

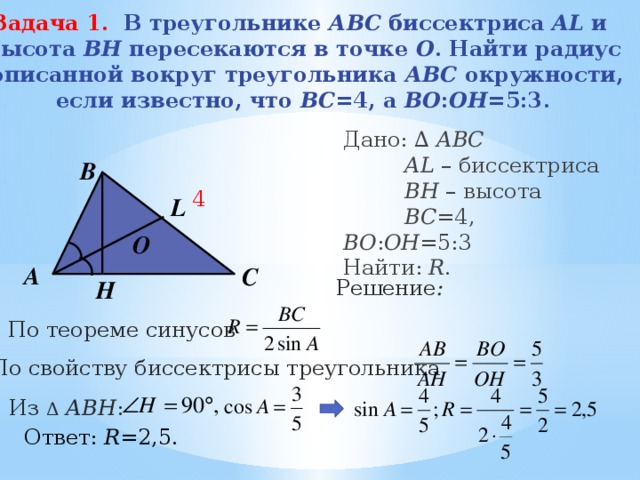
описанной вокруг треугольника АВС окружности,

По теореме синусов

По свойству биссектрисы треугольника

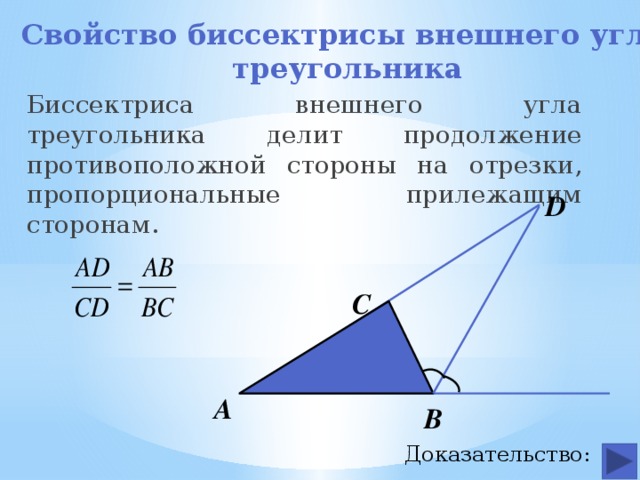
Свойство биссектрисы внешнего угла

Биссектриса внешнего угла треугольника делит продолжение противоположной стороны на отрезки, пропорциональные прилежащим сторонам.

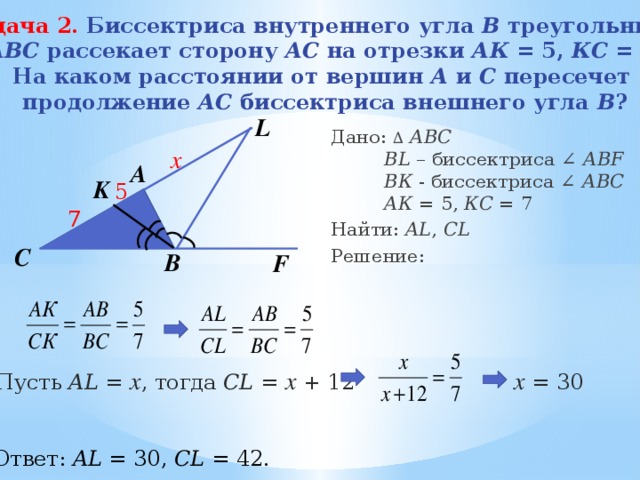
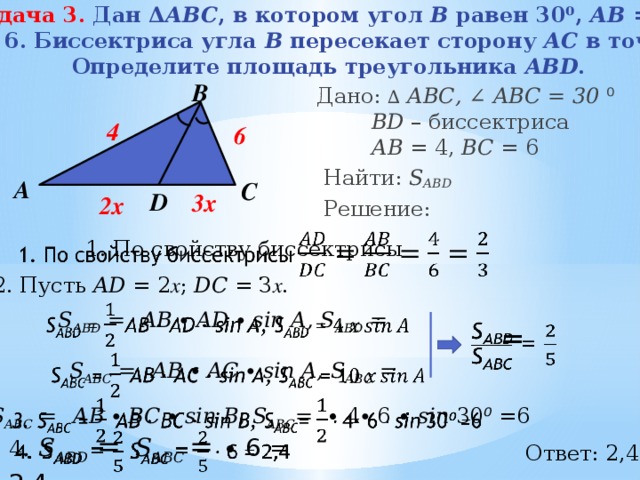
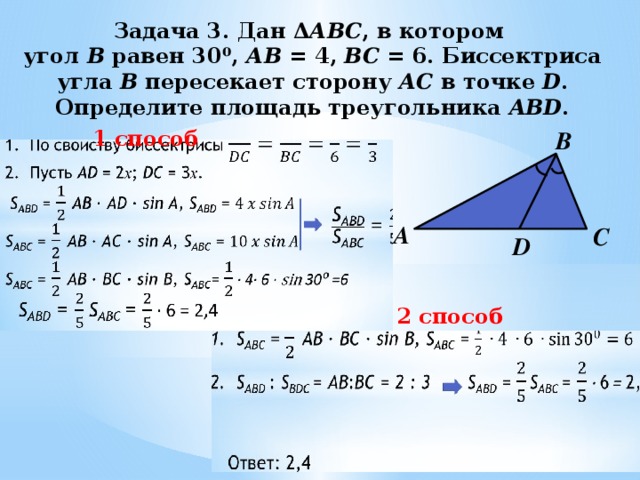
Задача 2. Биссектриса внутреннего угла В треугольника

Определите площадь треугольника ABD .

Дано: ∆ АВС, ∠ ABC = 30 ⁰ BD – биссектриса АB = 4, BС = 6

1. По свойству биссектрисы

Биссектриса угла треугольника делит его

площадь на части, пропорциональные

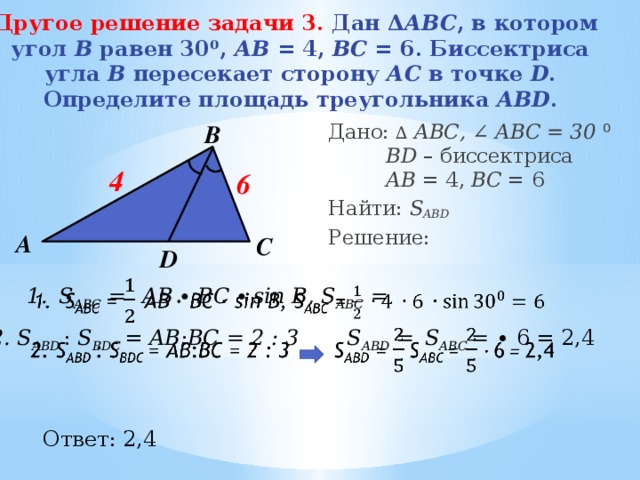
Другое решение задачи 3. Дан Δ АВС , в котором

Определите площадь треугольника ABD .

Дано: ∆ АВС, ∠ ABC = 30 ⁰ BD – биссектриса АB = 4, BС = 6

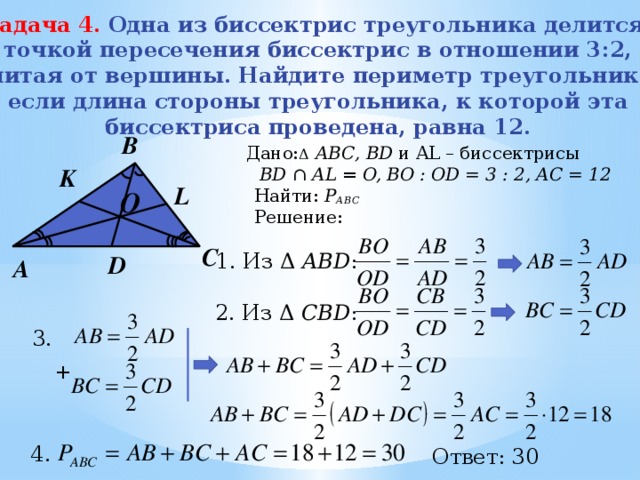
Задача 4. Одна из биссектрис треугольника делится

точкой пересечения биссектрис в отношении 3:2,

считая от вершины. Найдите периметр треугольника,

если длина стороны треугольника, к которой эта

биссектриса проведена, равна 12.

Дано: Δ АВС, BD и AL – биссектрисы

BD ∩ AL = O, BО : OD = 3 : 2, АС = 12

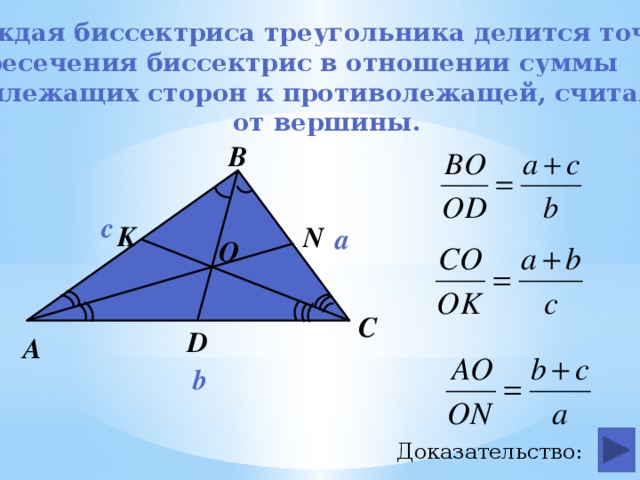
Малоизвестные свойства биссектрисы треугольника

Каждая биссектриса треугольника делится точкой

пересечения биссектрис в отношении суммы

прилежащих сторон к противолежащей, считая

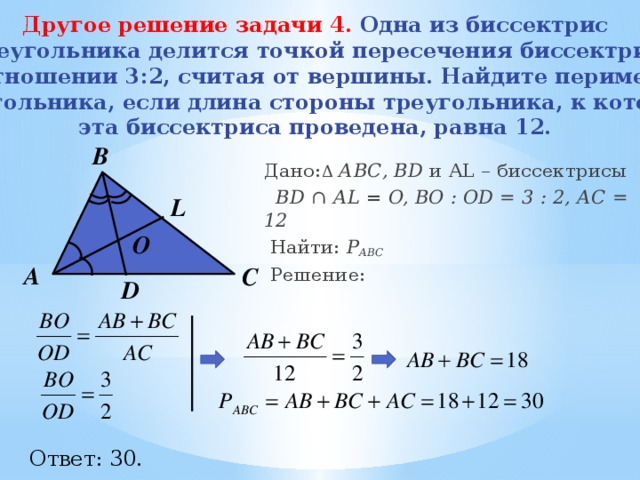
Другое решение задачи 4. Одна из биссектрис

треугольника делится точкой пересечения биссектрис

в отношении 3:2, считая от вершины. Найдите периметр

треугольника, если длина стороны треугольника, к которой

эта биссектриса проведена, равна 12.

Дано: Δ АВС, BD и AL – биссектрисы

BD ∩ AL = O, BО : OD = 3 : 2, АС = 12

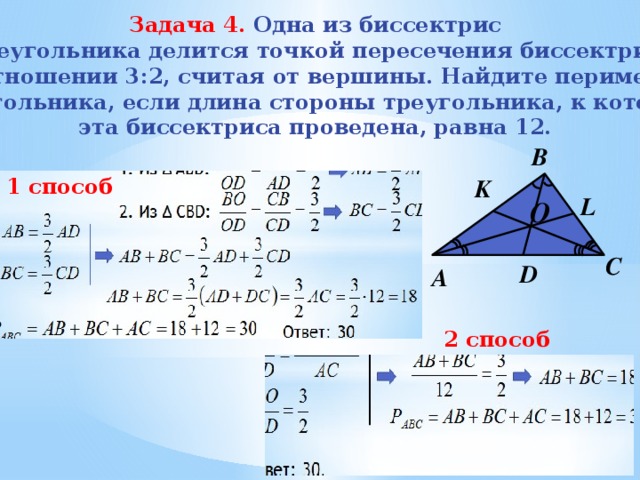
Задача 4. Одна из биссектрис

треугольника делится точкой пересечения биссектрис

в отношении 3:2, считая от вершины. Найдите периметр

треугольника, если длина стороны треугольника, к которой

эта биссектриса проведена, равна 12.

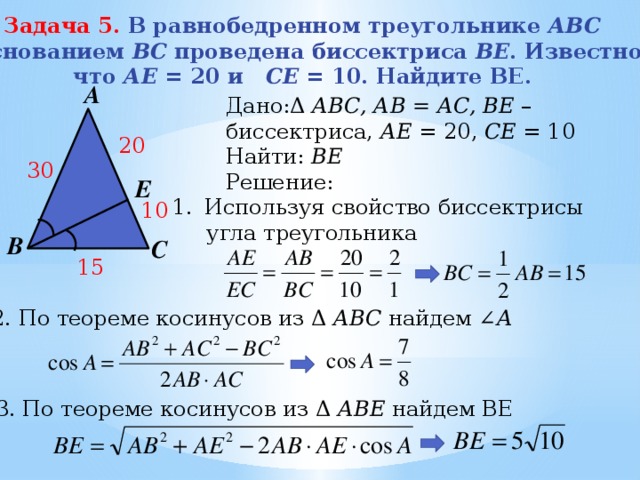
Задача 5. В равнобедренном треугольнике АBC

Дано:Δ АВС, АВ = АС, BE – биссектриса, АЕ = 20, СЕ = 10

2. По теореме косинусов из Δ АВС найдем ∠ А

3. По теореме косинусов из Δ АВЕ найдем ВЕ

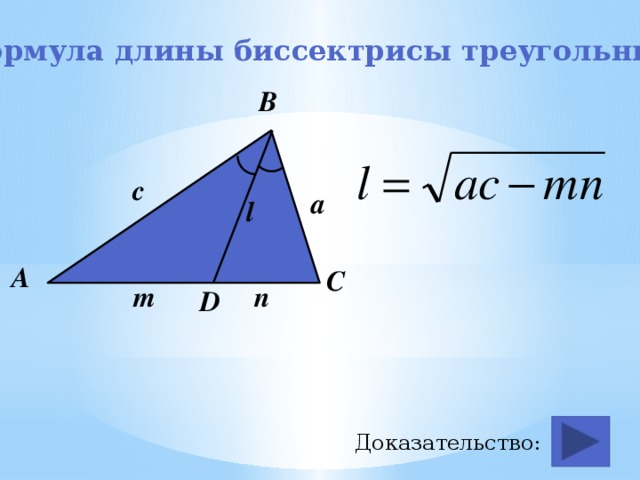
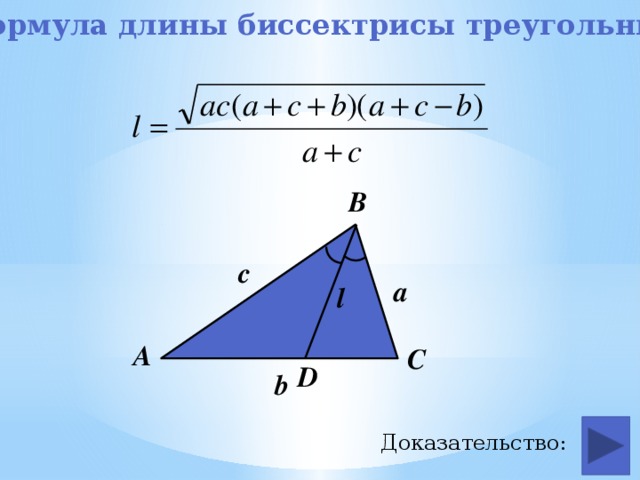
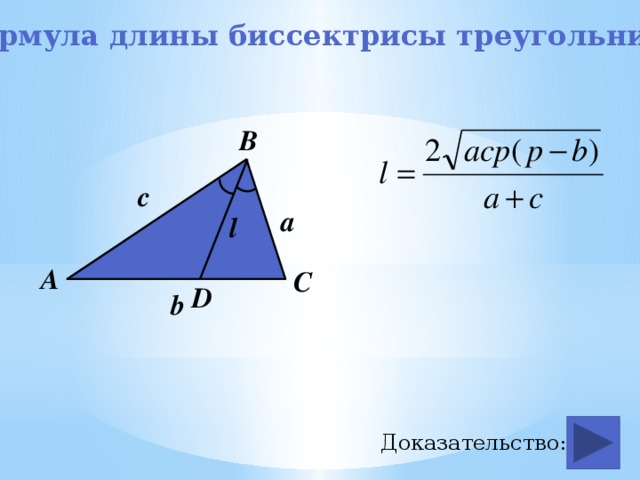
Формула длины биссектрисы треугольника

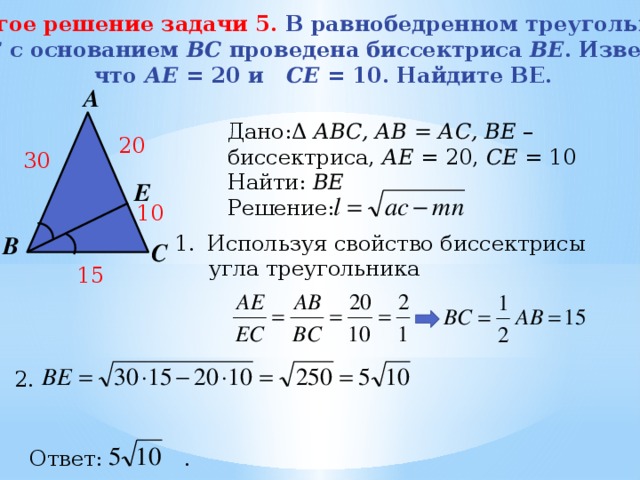
Другое решение задачи 5. В равнобедренном треугольнике

Дано:Δ АВС, АВ = АС, BE – биссектриса, АЕ = 20, СЕ = 10

Задача 5. В равнобедренном треугольнике

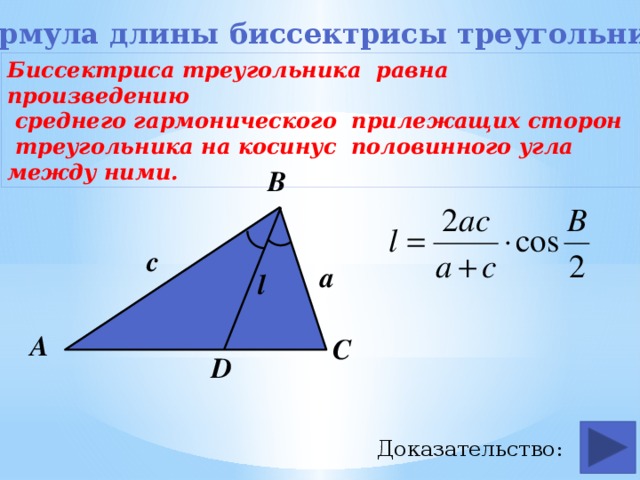
Формула длины биссектрисы треугольника

Биссектриса треугольника равна произведению

среднего гармонического прилежащих сторон

треугольника на косинус половинного угла между ними.

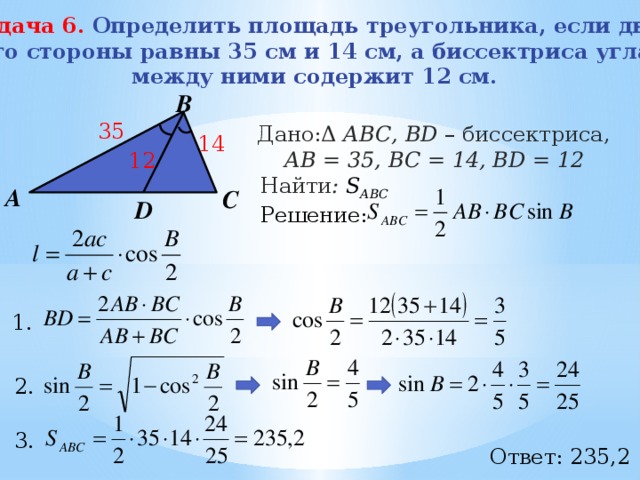
Задача 6. Определить площадь треугольника, если две

его стороны равны 35 см и 14 см, а биссектриса угла

между ними содержит 12 см.

Дано:Δ АВС, BD – биссектриса, АB = 35, BC = 14, ВD = 12

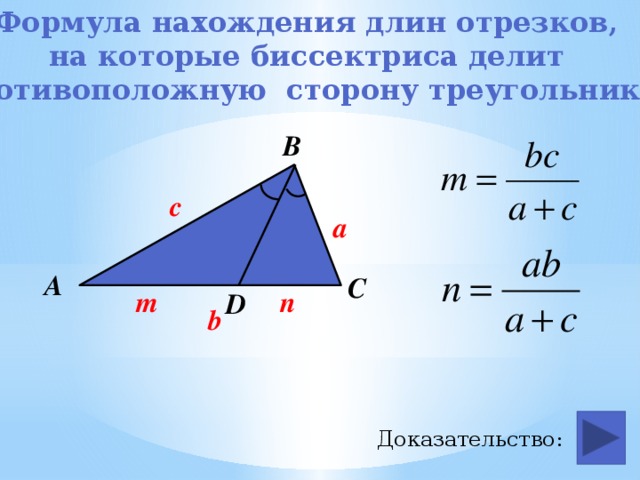
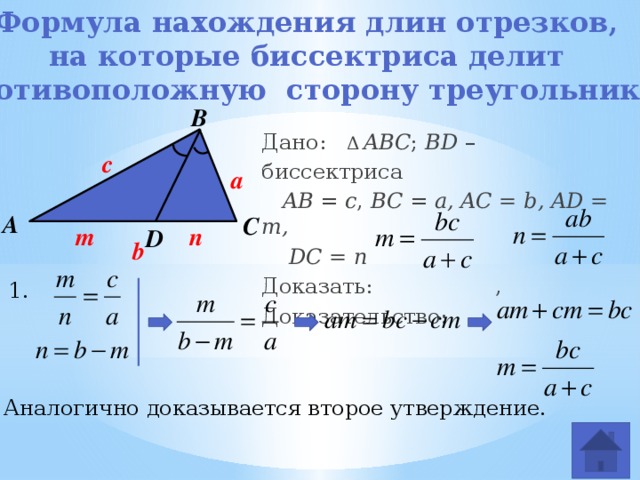
Формула нахождения длин отрезков,

на которые биссектриса делит

противоположную сторону треугольника

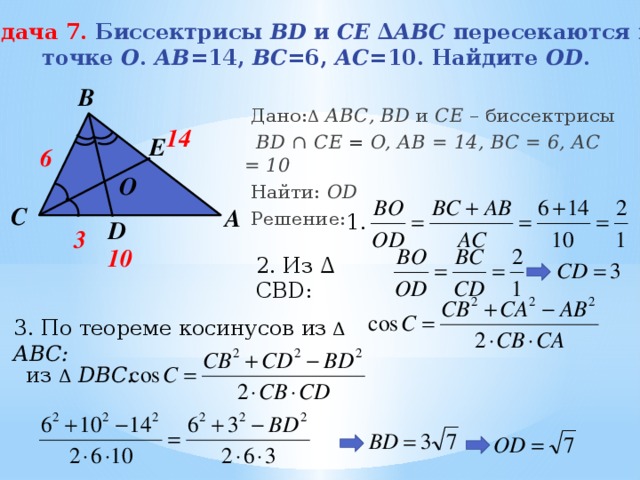
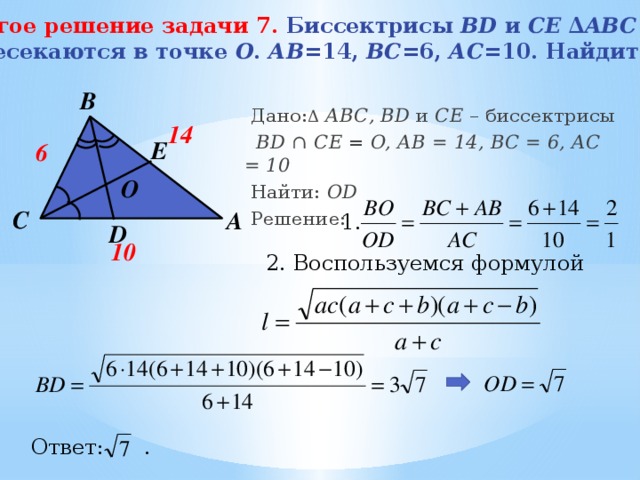
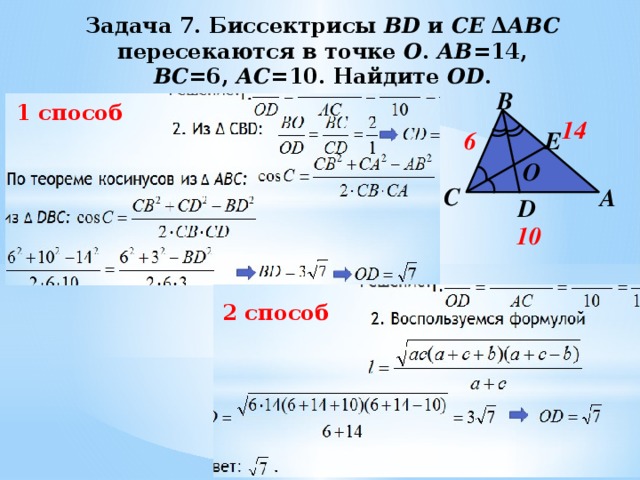
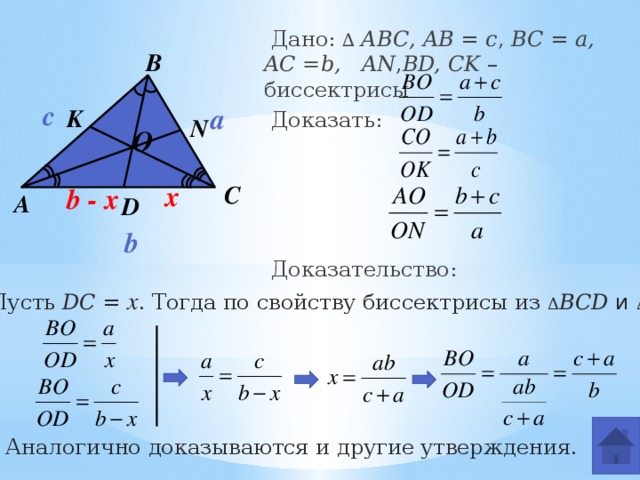
Дано: Δ АВС, BD и CE – биссектрисы

BD ∩ CE = O, АB = 14, BC = 6, AC = 10

3. По теореме косинусов из Δ АВС:

Формула длины биссектрисы треугольника

Формула длины биссектрисы треугольника

Дано: Δ АВС, BD и CE – биссектрисы

BD ∩ CE = O, АB = 14, BC = 6, AC = 10

2. Воспользуемся формулой

Свойства биссектрисы треугольника

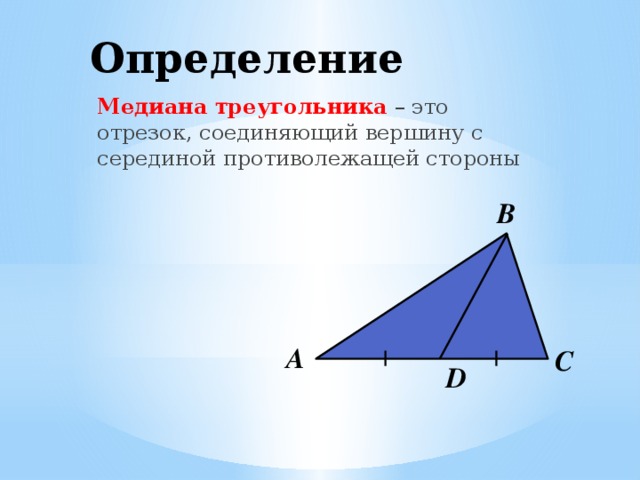
Что мы знаем о медиане треугольника из школьного учебника?

Медиана треугольника – это отрезок, соединяющий вершину с серединой противолежащей стороны

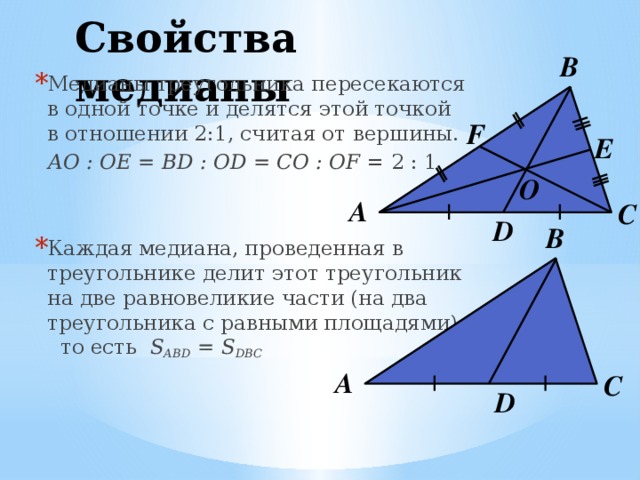
AO : OE = BD : OD = CO : OF = 2 : 1

Задача 8. Площадь треугольника АВС равна 198.

Найдите площадь четырехугольника MCLK , если известно,

Дано:Δ АВС, АВ = АС, BМ – медиана,

АL – биссектриса, S ABC = 198

1. По свойству медианы треугольника S ABM =S MBC = ∙ 198 = 99

2. По свойству биссектрисы треугольника

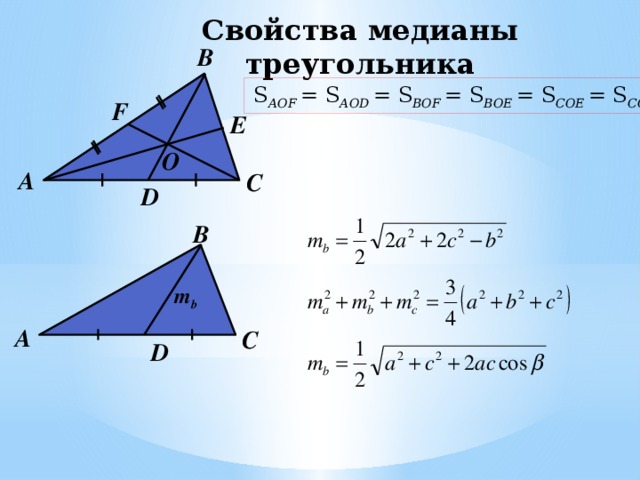
Малоизвестные свойства медианы треугольника

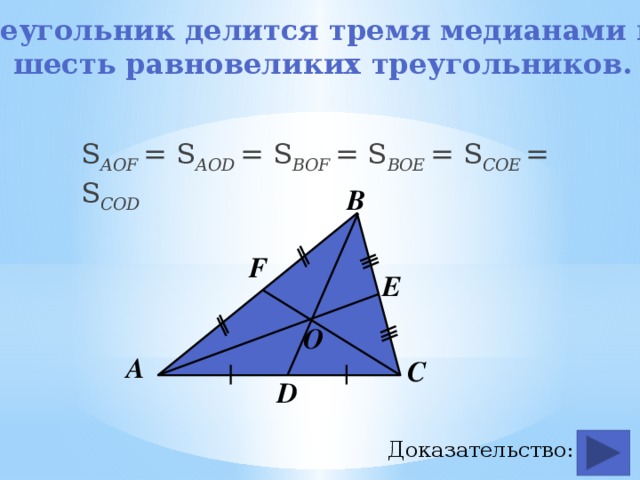
Треугольник делится тремя медианами на

шесть равновеликих треугольников.

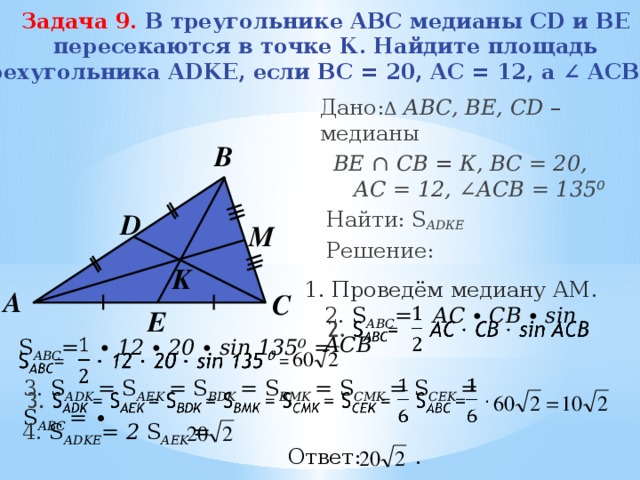
Задача 9. В треугольнике ABC медианы CD и BE

пересекаются в точке К. Найдите площадь

четырехугольника ADKE, если BC = 20, AC = 12, а ∠ ACB=135⁰.

Дано: Δ АВС, BE, CD – медианы

1. Проведём медиану АМ.

2. S АВС = АС ∙ СВ ∙ sin ACB

S АВС = ∙ 12 ∙ 20 ∙ sin 135⁰ =

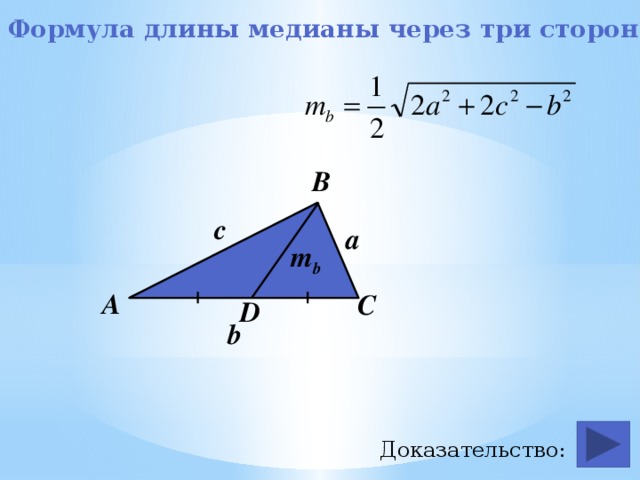
Формула длины медианы через три стороны .

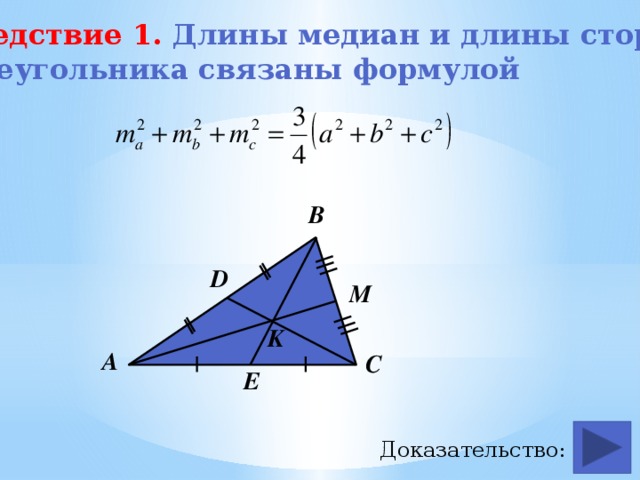
Следствие 1. Длины медиан и длины сторон

треугольника связаны формулой

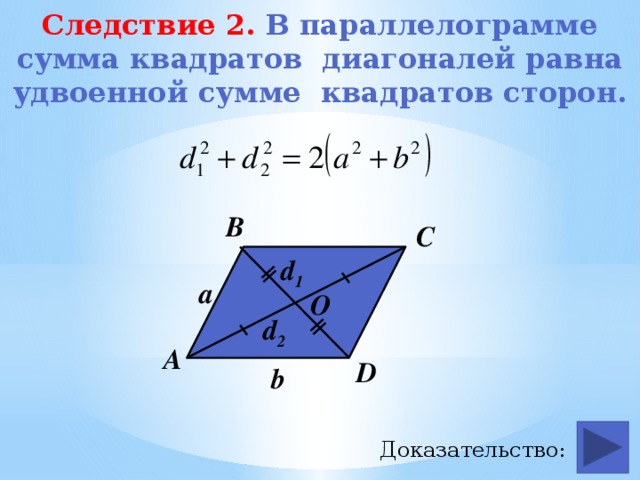
Следствие 2. В параллелограмме сумма квадратов диагоналей равна удвоенной сумме квадратов сторон.

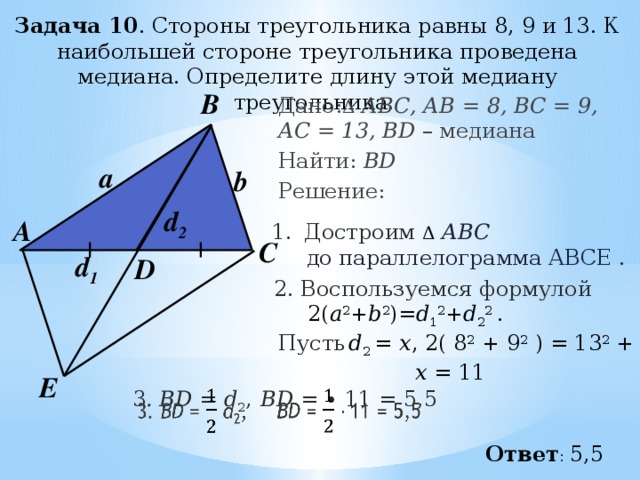
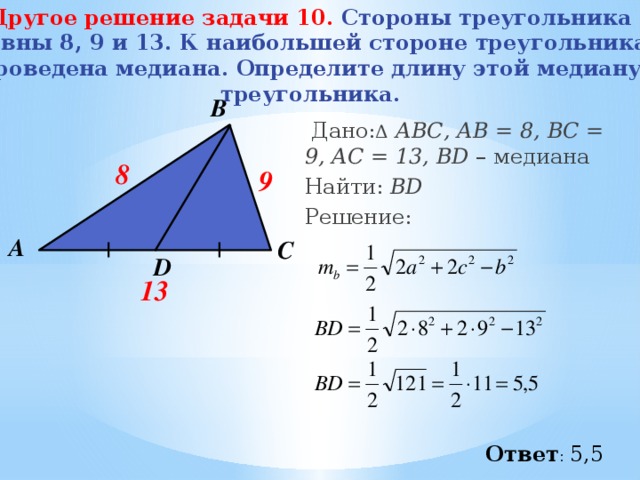
Дано: Δ АВС, АВ = 8, ВС = 9, АC = 13, BD – медиана

2. Воспользуемся формулой

Другое решение задачи 10. Стороны треугольника

равны 8, 9 и 13. К наибольшей стороне треугольника

проведена медиана. Определите длину этой медиану

Дано: Δ АВС, АВ = 8, ВС = 9, АC = 13, BD – медиана

Формула длины медианы через две стороны

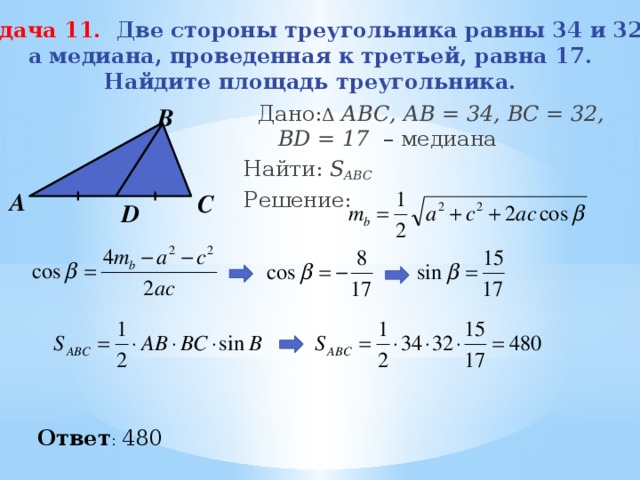
Задача 11. Две стороны треугольника равны 34 и 32,

а медиана, проведенная к третьей, равна 17.

Найдите площадь треугольника.

Дано: Δ АВС, АВ = 34, ВС = 32, BD = 17 – медиана

Свойства медианы треугольника

Спасибо за внимание

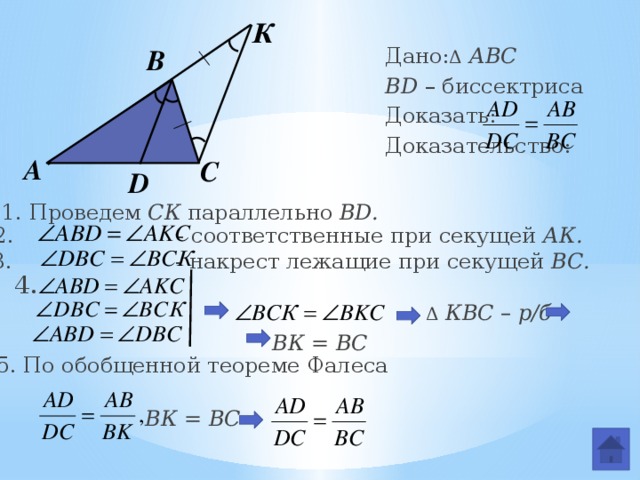
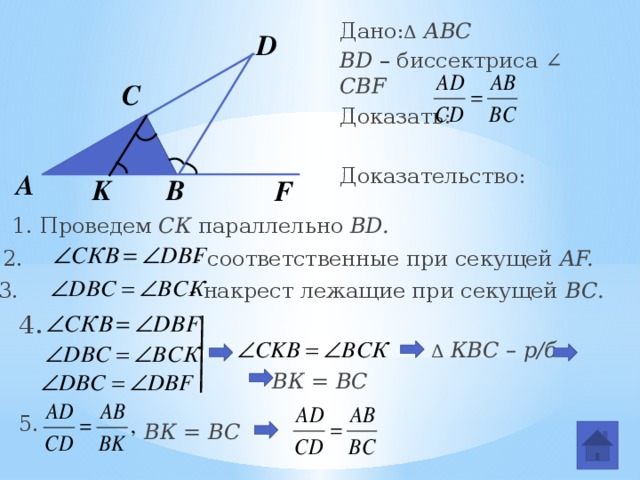
1. Проведем СК параллельно BD.

5. По обобщенной теореме Фалеса

BD – биссектриса ∠ CBF

1. Проведем СК параллельно BD.

2. Аналогично доказываются и другие утверждения.

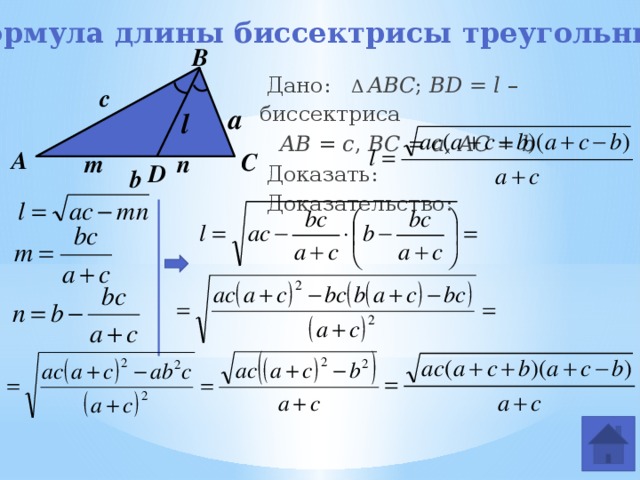
Формула длины биссектрисы

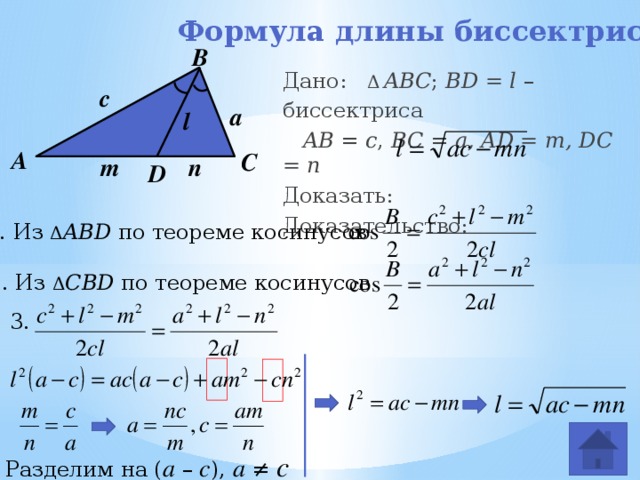
Дано: Δ ABC ; BD = l – биссектриса

1. Из Δ ABD по теореме косинусов

2. Из Δ СBD по теореме косинусов

Формула длины биссектрисы треугольника

Дано: Δ ABC ; BD = l – биссектриса

Формула нахождения длин отрезков,

на которые биссектриса делит

противоположную сторону треугольника

Дано: Δ ABC ; BD – биссектриса

2. Аналогично доказывается второе утверждение.

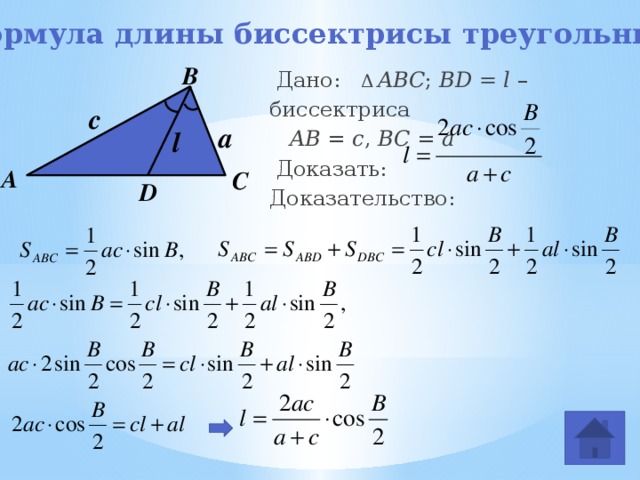
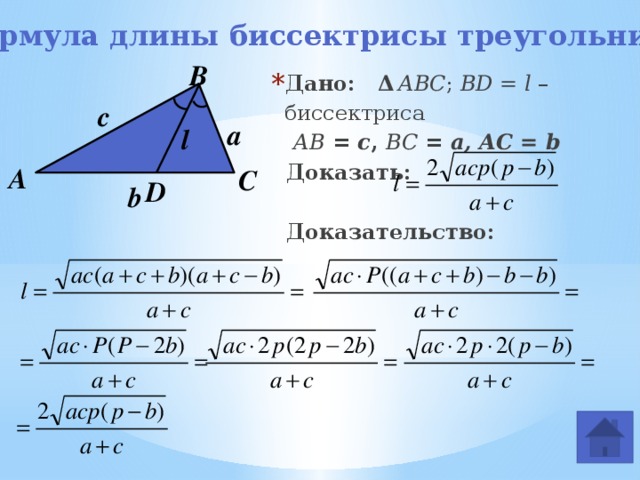
Формула длины биссектрисы треугольника

Дано: Δ ABC ; BD = l – биссектриса

Формула длины биссектрисы треугольника

Треугольник делится тремя медианами на

шесть равновеликих треугольников.

Дано: Δ АВС, AE, BD, CF, – медианы

2. S АOD = АO ∙ OD ∙ sin AOD =

OE ∙ OB ∙sin BOE = S BOE

Формула длины медианы треугольника

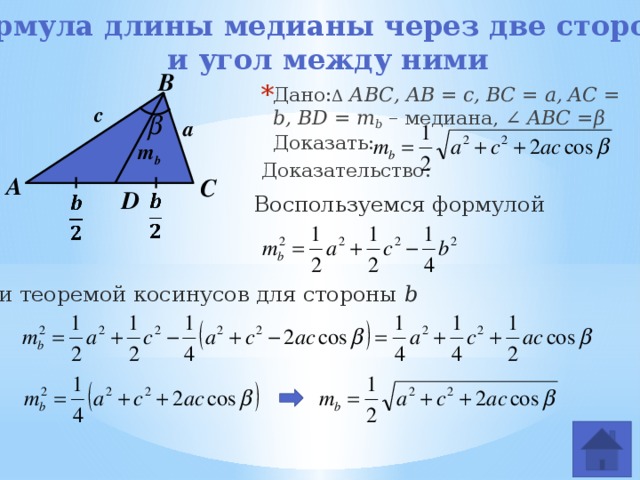
Дано: Δ АВС, AB = c, BC = a, AC = b, BD = m b – медиана

2. Сложим полученные равенства:

Следствие 1. Длины медиан и длины сторон

треугольника связаны формулой

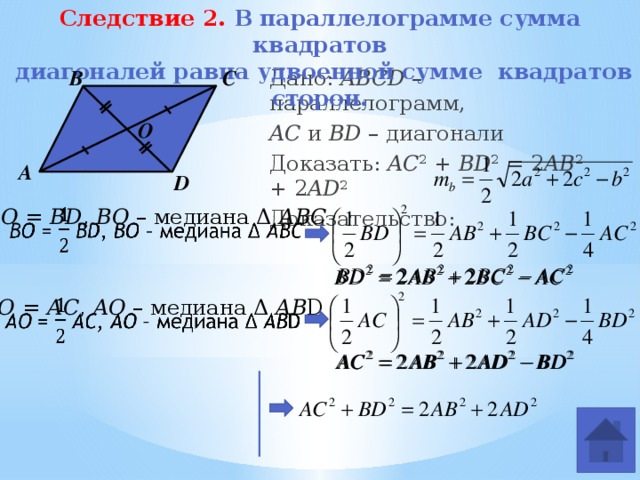
Следствие 2. В параллелограмме сумма квадратов

диагоналей равна удвоенной сумме квадратов сторон.

Дано: ABCD –параллелограмм,

AC и BD – диагонали

Доказать: AC 2 + BD 2 = 2 AB 2 + 2 AD 2

Формула длины медианы через две стороны

Источник

В треугольнике abc проведена биссектриса ad найдите bd если известно что

В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.

а) докажите, что биссектриса угла С делит отрезок МN пополам

б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.

а) Обозначим K точку пересечения отрезков AM и BN. Треугольник ABN равнобедренный, так как в нем AK является биссектрисой и высотой. Следовательно, AK является и медианой, то есть K — середина BN. Получаем, что AN = AB = 6, откуда NC = AC − AN = 3.

Рассмотрим треугольник ABC, биссектриса делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам: BM : MC = AB : AC, учитывая, что длина BC равна 5, получаем: BM = 2; MC = 3.

В треугольнике MNC стороны NC и MC равны, следовательно, треугольник MNC — равнобедренный, с основанием MN. Значит, биссектриса угла C также является медианой и высотой. Таким образом, получаем, что биссектриса угла С делит отрезок MN пополам.

б) Рассмотрим треугольник PMN: отрезок PO перпендикулярен прямой MN и делит её пополам, следовательно, треугольник PMN — равнобедренный с основанием MN. Значит, PM = PN и отношение AP : PN = AP : PM.

В треугольнике AMC отрезок CP — биссектриса, поэтому AP : PM = AC : MC = 3 : 1.

Приведем другое решение.

а) Обозначим за K точку пересечения отрезков AM и BN. Треугольник ABN равнобедренный, так как в нем AK является биссектрисой и высотой. Следовательно, AK является и медианой, то есть K — середина BN. Получаем, что AN = AB = 6, откуда NC = AC − AN = 3.

Далее, в видим, что KM является высотой и медианой, откуда следует, что треугольник BMN равнобедренный. Обозначим BM = MN = x, тогда MC = BC − BM = 5 − x.

Из по теореме косинусов получаем:

Из треугольника по теореме косинусов: откуда:

Таким образом, получили, что MN = 2, MC = 3 — значит, треугольник MCN равнобедренный, откуда следует, что биссектриса CO является и высотой, и медианой. Значит, точка O — середина стороны MN. Что и требовалось доказать.

б) Опустим вспомогательный перпендикуляр из точки P на сторону AN (пересечение в точке H). Отрезок PH является радиусом вписанной окружности, так как P — точка пересечения биссектрис (а значит — центр вписанной окружности). Найдем радиус из формулы где S — площадь треугольника ABC, p — полупериметр треугольника, равный

Найдем площадь по формуле Герона:

Тогда

Из треугольника ABC вновь по теореме косинусов найдем косинус угла A (обозначим его за ):

Так как то

откуда

Тогда из получаем:

Найдем, что HN = AN − AH = 1, тогда из по теореме Пифагора:

Окончательно получаем, что

Дублирует задание 505501.