В треугольнике abc проведены медианы aa1 и bb1 оказалось что aa1 6
В треугольнике abc проведены медианы aa1 и bb1 оказалось что aa1 6
Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 10.
Известно, что медианы делятся точкой пересечения в отношении 2:1, считая от вершины. Значит,
Поэтому треугольники AB1B и CB1B равнобедренные, причём ∠B1AB = ∠ABB1 и ∠B1CB = ∠CBB1. Сумма всех этих четырёх углов равна 180°. Тогда ∠ABC = ∠ABB1 + ∠CBB1 = 90°. Следовательно, треугольник ABC — прямоугольный.
б) Треугольник A1BA прямоугольный. Поэтому
Аналогично из прямоугольного треугольника C1BC находим:
Тогда 
Приведём другое решение пункта а).
Покажем, что медиана, проведенная к стороне AC, равна половине этой стороны. Тогда угол, противолежащий стороне AC, равен 90°, что и требуется доказать. Действительно, медианы делятся точкой пересечения в отношении 2:1, считая от вершины. Значит,
В треугольнике abc проведены медианы aa1 и bb1 оказалось что aa1 6
Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 8.
а) Известно, что медианы треугольника точкой пересечения делятся в отношении 2 :1, считая от вершины. Значит,
Поэтому треугольники 
и 
равнобедренные, причём 
и 
Сумма всех этих четырёх углов равна 180°. Тогда 
Отсюда следует, что треугольник ABC прямоугольный.
б) Треугольник 
прямоугольный. Поэтому
Аналогично, из прямоугольного треугольника 
находим:
Сложим полученные равенства:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
Аналоги к заданию № 505537: 509323 509344 511579 Все
Докажите §6 №74 ГДЗ Геометрия 7-9 класс Погорелов А.В.
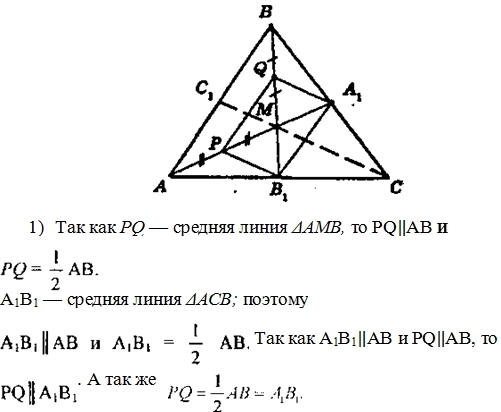
1) В треугольнике АВС проведены медианы АА1 и ВВ1,
которые пересекаются в точке М. В треугольнике АМВ проведена средняя линия PQ. Докажите, что четырехугольник А1B1PQ — параллелограмм.
2) Докажите, что любые две медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины.
3) Докажите, что все три медианы треугольника пересекаются в одной точке.
Значит, четырехугольник A1B1PQ — параллелограмм, так как две его стороны параллельны и равны, чем доказано первое утверждение.
1) Докажем, что медианы АА1 и BB1 в точке пересечения делятся в отношении 2:1, считая от вершины. PQ — средняя линия ΔАМB, следовательно АР = PM = х; BQ = QM = у. Выше мы доказали, что A1B1PQ — параллелограмм, значит, его диагонали в точке пересечения делятся пополам, то есть A1M = РМ = х и B1M=MQ=Y.
Получаем
BММВ1 = 2у:у = 2:1,
AM: MA1 =2х:х = 2:1;
Чем доказано второе утверждение задачи.
Проведем третью медиану СС1, которая пересекает медиану АА1 в некоторой точке и, согласно доказанному во второй части задачи, эта точка должна делить медиану AA1 в отношении 2:1, считая от точки А. Так как положение такой точки на отрезке определяется однозначно, то она совпадает с точкой М. Значит, СС1 проходит через точку М. То есть все три медианы пересекаются в одной точке. Что и требовалось доказать.
В треугольнике abc проведены медианы aa1 и bb1 оказалось что aa1 6
Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 10.
Известно, что медианы делятся точкой пересечения в отношении 2:1, считая от вершины. Значит,
Поэтому треугольники AB1B и CB1B равнобедренные, причём ∠B1AB = ∠ABB1 и ∠B1CB = ∠CBB1. Сумма всех этих четырёх углов равна 180°. Тогда ∠ABC = ∠ABB1 + ∠CBB1 = 90°. Следовательно, треугольник ABC — прямоугольный.
б) Треугольник A1BA прямоугольный. Поэтому
Аналогично из прямоугольного треугольника C1BC находим:
Тогда
Приведём другое решение пункта а).
Покажем, что медиана, проведенная к стороне AC, равна половине этой стороны. Тогда угол, противолежащий стороне AC, равен 90°, что и требуется доказать. Действительно, медианы делятся точкой пересечения в отношении 2:1, считая от вершины. Значит,
В треугольнике ABC медиана AA1 является высотой, значит, треугольник ABC является равнобедренным и AB = AC.
