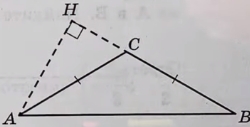
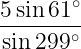В тупоугольном треугольнике abc известно что ac bc 10 высота ah 7

Решение Ященко ЕГЭ 2022 (профиль) Вариант №1 (36 вариантов) Математика

Решение и ответы заданий Варианта №1 из сборника ЕГЭ 2022 по математике (профильный уровень) И.В. Ященко. ГДЗ Решебник профиль для 11 класса. Полный разбор. Ответы с решением.

Задание 2.
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,1. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Задание 3.
В тупоугольном треугольнике ABC известно, что AC = BC = 10, высота AH равна √51. Найдите косинус угла ACB.

Задание 4.
Найдите значение выражения

Задание 5.
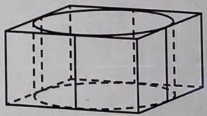
Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.

Задание 6.
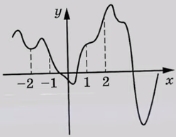
На рисунке изображён график функции 𝑦 = 𝑓(𝑥). На оси абсцисс отмечены точки −2, –1, 1, 2. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

Задание 7.
При температуре 0°С рельс имеет длину 𝑙₀ = 10 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону 𝑙(𝑡°) = 𝑙₀(1 + 𝛼∙𝑡°), где 𝛼 = 1,2∙10 −5 (°С ) −1 – коэффициент теплового расширения, 𝑡° – температура (в градусах Цельсия). При какой температуре рельс удлинится на 6 мм? Ответ дайте в градусах Цельсия.

Задание 8.
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 105 км. На следующий день он отправился обратно в А со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в B. Найдите скорость велосипедиста на пути из B в А. Ответ дайте в км/ч.

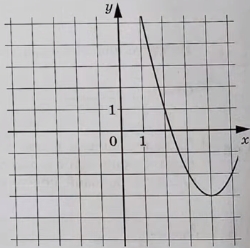
Задание 9.
На рисунке изображён график функции вида f(x) = ax 2 + bx + c, где числа a, b и c – целые. Найдите значение f (−5).

Задание 10.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 30% этих стекол, вторая – 70%. Первая фабрика выпускает 5% бракованных стекол, а вторая – 4%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Задание 11.
Найдите наименьшее значение функции y = \frac<4> <3>x√x – 3x + 9 на отрезке [0,25; 30].

Задание 13.
Дана правильная треугольная пирамида SABC, сторона основания AB = 16, высота SH = 10, точка K – середина бокового ребра SА. Плоскость, параллельная плоскости АВС, проходит через точку K и пересекает ребра SB и SC в точках Q и P соответственно.

а) Докажите, что площадь четырёхугольника BCPQ составляет \frac<3> <4>площади треугольника SBC
б) Найдите объем пирамиды KBCPQ.

Задание 14.
Решите неравенство (4 х – 5·2 х ) 2 – 20(4 х – 5·2 х ) ≤ 96.

Задание 15.
В июле 2025 года планируется взять кредит на 8 лет. Условия его возврата таковы:
– в январе 2026, 2027, 2028, 2029 годов долг возрастает на 20% по сравнению с концом предыдущего года;
– в январе 2030, 2031, 2032, 2033 годов долг возрастает на 18% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года должен быть на одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2033 года долг должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат до полного его погашения составит 1125 тысяч рублей?

Задание 16.
Точки A, B, C, D и E лежат на окружности в указанном порядке, причем AE = ED = CD, а прямые AC и BE перпендикулярны. Отрезки AC и BD пересекаются в точке T.

а) Докажите, что прямая EC пересекает отрезок TD в его середине.
б) Найдите площадь треугольника ABT, если BD = 6, АЕ = √6.

Задание 17.
Найдите все значения 𝑎, при каждом из которых уравнение

имеет ровно один корень.

Задание 18.
На доске написаны три различных натуральных числа. Второе число равно сумме цифр первого, а третье равно сумме цифр второго.

а) Может ли сумма этих чисел быть равна 2022?
б) Может ли сумма этих чисел быть равна 2021?
в) В тройке чисел первое число трёхзначное, а третье равно 2. Сколько существует таких троек?

Источник варианта: Сборник ЕГЭ 2022. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.

Источник

В тупоугольном треугольнике abc известно что ac bc 10 высота ah 7

БАЗА ЗАДАНИЙ

Задание № 3. Планиметрия.

1. У треугольника со сторонами 12 и 15 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 10. Найдите длину высоты, проведенной ко второй стороне.

2. В треугольнике ABC угол A равен 56°, углы B и C – острые, высоты BD и CE пересекаются в точке O. Найдите угол DOE. Ответ дайте в градусах.

3. В треугольнике ABC угол C равен 66°, биссектрисы AD и BE пересекаются в точке O. Найдите угол AOB. Ответ дайте в градусах.

4. Угол A прямоугольного треугольника равен 64°. Найдите угол AOE, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.

5. В треугольнике ABC AC=BC, AB=20, высота AH равна 8. Найдите синус угла BAC.

6. В треугольнике ABC AC = BC, AB = 8, sin∠BAC = 0,5. Найдите высоту AH.

7. В треугольнике ABC известно, что AC = BC, AH – высота, sin∠BAC=7/25. Найдите sin∠BAH.

8. В треугольнике ABC известно, что AC = BC, AH – высота, tg∠BAC=7/24. Найдите cos∠BAH.

9. В треугольнике ABC известно, что AC = BC=4√15, cos∠BAC=0,25. Найдите высоту AH.

10. В треугольнике ABC угол C равен 90°, AB=10, AC=√51. Найдите sin∠A.

11. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 11. Найдите площадь этого треугольника.

12. В прямоугольном треугольнике угол между высотой и биссектрисой, проведёнными из вершины прямого угла, равен 14°. Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.

13. Острые углы прямоугольного треугольника равны 84° и 6°. Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

14. Угол между биссектрисой и медианой прямоугольного треугольника, проведёнными из вершины прямого угла, равен 14°. Найдите меньший угол прямоугольного треугольника.

15. В треугольнике ABC CD — медиана, угол C равен 90°, угол B равен 35°. Найдите угол ACD. Ответ дайте в градусах.

16. В треугольнике ABC AC=BC=20, AB=28. Найдите косинус угла A.

18. В треугольнике ABC AC = BC = 5, sin∠A =0,8. Найдите АВ.

19. В равностороннем треугольнике ABC высота CH равна 45√3. Найдите AB.

20. В треугольнике ABC известно, что AC = BC, AB = 1, cos∠A= √17 / 17. Найдите высоту CH.

21. В треугольнике ABC известно, что AC = BC, AB = 16, tg∠A=0,5. Найдите высоту CH.

22. В треугольнике ABC известно, что AC = BC, AB = 4, высота CH=2√3. Найдите угол С.

23. В треугольнике ABC угол C равен 90°, AC=6, tg∠A=√5 / 2. Найдите AB.

24. В треугольнике ABC стороны AC и BC равны, угол C равен 156°, угол CBD – внешний. Найдите угол CBD. Ответ дайте в градусах.

25. В прямоугольном треугольнике АВС из вершины прямого угла проведена медиана CD, причем величины углов BDC и ADC относятся как 4:5. Найдите величину угла А в градусах.

26. Высота AD треугольника АВС делит противоположную сторону на части: CD = 4, BD =1,5. Найдите длину стороны АC, если tg∠B = 2.

27. В треугольнике ABC угол C равен 90°, CH — высота, BC = 8, sin∠A=0,5. Найдите BH.

28. В треугольнике ABC угол C равен 90°, AB = 5, cos∠A = 0,6. Найдите высоту CH.

29. В треугольнике ABC угол C равен 90°, угол A равен 30°, AB=2√3. Найдите высоту CH.

30. В треугольнике ABC угол C равен 90°, CH — высота, BC = 3, cos∠A= √35 / 6. Найдите AH.

31. В треугольнике ABC угол C равен 90°, CH — высота, AB = 13, tg∠A = 1/5. Найдите AH.

32. В треугольнике ABC угол C равен 90°, AB = 13, tg∠A = 1/5. Найдите высоту CH.

33. В треугольнике ABC угол C равен 90°, CH — высота, BC = 25, BH = 20. Найдите cos∠A.

34. В тупоугольном треугольнике ABC AC = BC=8, высота AH равна 4. Найдите sin∠ACB.

35. В тупоугольном треугольнике ABC AC = BC, AB = 10, высота AH равна 8. Найдите sin∠BAC.

36. В тупоугольном треугольнике ABC AC = BC, AB = 5, высота AH равна 4. Найдите cos∠BAC.

37. В треугольнике ABC угол C равен 90°, синус ∠В=7/25. Найдите синус внешнего угла при вершине А.

38. В треугольнике ABC угол C равен 90°, косинус угла В=0,6. Найдите косинус внешнего угла при вершине А.

41. В треугольнике ABC AC=BC=√17, AB=8. Найдите тангенс внешнего угла при вершине В.

43. Один из внешних углов треугольника равен 85°. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.

44. В треугольнике ABC угол A равен 60°, угол B равен 70°, CH — высота. Найдите разность углов ACH и BCH. Ответ дайте в градусах.

45. В треугольнике ABC угол A равен 30°, CH — высота, угол BCH равен 22°. Найдите угол ACB. Ответ дайте в градусах.

46. В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.

Источник

В тупоугольном треугольнике abc известно что ac bc 10 высота ah 7

В тупоугольном треугольнике ABC высота AH равна 1. Найдите

Это задание ещё не решено, приводим решение прототипа.

В тупоугольном треугольнике ABC высота AH равна 4. Найдите

Выразим площадь треугольника двумя способами:

Отсюда имеем:

Приведём другое решение.

Синусы смежных углов равны, поэтому

В тупоугольном треугольнике ABC высота AH равна 7. Найдите

Это задание ещё не решено, приводим решение прототипа.

В тупоугольном треугольнике ABC высота AH равна 4. Найдите

Выразим площадь треугольника двумя способами:

Отсюда имеем:

Приведём другое решение.

Синусы смежных углов равны, поэтому

В тупоугольном треугольнике ABC высота AH равна 2. Найдите

Это задание ещё не решено, приводим решение прототипа.

В тупоугольном треугольнике ABC высота AH равна 4. Найдите

Выразим площадь треугольника двумя способами:

Отсюда имеем:

Приведём другое решение.

Синусы смежных углов равны, поэтому

В тупоугольном треугольнике ABC высота AH равна 2. Найдите

Это задание ещё не решено, приводим решение прототипа.

В тупоугольном треугольнике ABC высота AH равна 4. Найдите

Выразим площадь треугольника двумя способами:

Отсюда имеем:

Приведём другое решение.

Синусы смежных углов равны, поэтому

В тупоугольном треугольнике ABC высота AH равна 5. Найдите

Это задание ещё не решено, приводим решение прототипа.

В тупоугольном треугольнике ABC высота AH равна 4. Найдите

Выразим площадь треугольника двумя способами:

Отсюда имеем:

Приведём другое решение.

Синусы смежных углов равны, поэтому

В тупоугольном треугольнике ABC высота AH равна 3. Найдите

Это задание ещё не решено, приводим решение прототипа.

В тупоугольном треугольнике ABC высота AH равна 4. Найдите

Выразим площадь треугольника двумя способами:

Отсюда имеем:

Приведём другое решение.

Синусы смежных углов равны, поэтому

В тупоугольном треугольнике ABC высота AH равна 2. Найдите

Это задание ещё не решено, приводим решение прототипа.

В тупоугольном треугольнике ABC высота AH равна 4. Найдите

Выразим площадь треугольника двумя способами:

Отсюда имеем:

Приведём другое решение.

Синусы смежных углов равны, поэтому

В тупоугольном треугольнике ABC высота AH равна 2. Найдите

Это задание ещё не решено, приводим решение прототипа.

В тупоугольном треугольнике ABC высота AH равна 4. Найдите

Выразим площадь треугольника двумя способами:

Отсюда имеем:

Приведём другое решение.

Синусы смежных углов равны, поэтому

В тупоугольном треугольнике ABC высота AH равна 9. Найдите

Это задание ещё не решено, приводим решение прототипа.

В тупоугольном треугольнике ABC высота AH равна 4. Найдите

Выразим площадь треугольника двумя способами:

Отсюда имеем:

Приведём другое решение.

Синусы смежных углов равны, поэтому

В тупоугольном треугольнике ABC высота AH равна 10. Найдите

Это задание ещё не решено, приводим решение прототипа.

В тупоугольном треугольнике ABC высота AH равна 4. Найдите

Выразим площадь треугольника двумя способами:

Отсюда имеем:

Приведём другое решение.

Синусы смежных углов равны, поэтому

Источник