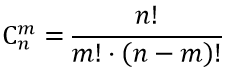Бросается 10 монет найти вероятность что число выпавших гербов будет равно шести
Формула Бернулли
Если в n испытаниях событие А случается (происходит) k раз и не случается (не происходит) (n-k) раз, то данную вероятность Рn(k) можно найти по формуле Бернулли:
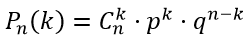
где
p — вероятность успеха испытания (опыта);
q=1-p — вероятность неудачи испытания (вероятность противоположного события);
$C_n^k$ — число сочетаний, вычисляется по формуле комбинаторики — сочетание без повторения
Пример 1
Монету бросают шесть раз. Найти вероятность того, что герб выпадет не менее двух раз.
Пример 2
Каждый день акции компании X поднимаются в цене или падают в цене на один пункт с вероятностями 0,75 и 0,25. Найти вероятность того, что акции после 6 дней вернутся к своей первоначальной цене, то есть чтобы акции за это время 3 раза поднялись в цене и три раза опустились в цене. При этом изменения цены акции вверх и вниз – независимые события.
Решение
Пример 4
Два равносильных противника играют в шахматы.
Что вероятнее:
а) выиграть одну партию из двух или две партии из четырех?
б) выиграть не менее двух партий из четырех или не менее трех партий из пяти? Ничьи во внимание не принимаются.
Решение
Вероятность выигрыша шахматиста равна р=1/2, а вероятность проигрыша шахматиста
q=1-p=0.5
а) По формуле Бернулли найдём вероятность P2(1) «выиграть одну партию из двух» и вероятность P4(2) «выиграть две партии из четырех»
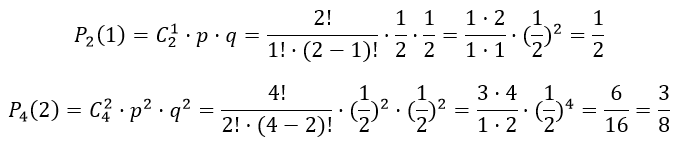
Имеем P2(1)>Р4(2) следовательно, вероятнее в шахматы выиграть одну партию из двух, чем две партии из четырех.
б) Сначала рассмотрим событие A — «выиграть не менее двух партий из четырех», которое соответствует сумме независимых событий Р4(2), Р4(3), Р4(3), то есть «выиграть две или три или четыре партии из четырех»
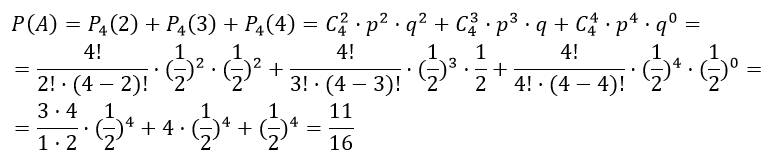
Теперь рассмотрим событие В — «выигрыш не менее трех партий из пяти», которое соответствует сумме независимых событий Р5(3), Р5(4), Р5(5), то есть «выиграть три или четыре или пять партий из трех»
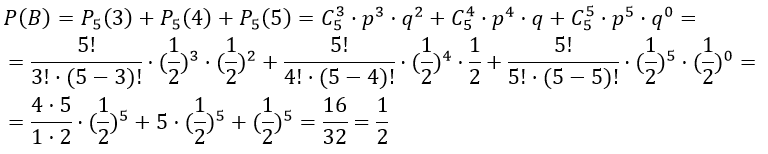
Здесь Р(А)>P(B), следовательно, вероятнее выиграть не менее двух партий из четырех, чем не менее трех партий из пяти.
Практическая работа по теории вероятностей и математической статистике по теме: «Вычисление вероятностей по формуле Бернулли»
Учебная дисциплина «Теория вероятностей и математическая статистика»
специальность среднего профессионального образования
230401 Информационные системы (по отраслям)
Тема: «Вычисление вероятностей по формуле Бернулли»
Методические указания и теоретические сведения к практической работе
Цель: 1) Расширение и углубление знаний о вероятности события при независимых испытаниях.
2) Формирование умений решать задачи на нахождение вероятности с использованием формулы Бернулли
3) Формированию ОК 2,3,4
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
P 4 (2) = C 4 2 ·p 2 ·q 2 =(12/2)·(2/3) 2 ·(1/3) 2 = 8/27
Задача 2. Игральную кость бросили 10 раз. Какова вероятность, что число 3 выпадет два раза?
Решение. При одном броске вероятность выпадения тройки равна р = 1/6, а вероятность не выпадения равна 1-р = 5/6.
Р= С 10 2 ·(1/6) 2 ·(5/6) 8 = 10!/ (8!*2!)* 5 8 /6 10 = 45*5 8 /6 10 ≈0,29
Задача 3.
Вероятность появления события А равна 0,4. Какова вероятность того, что при 10 испытаниях событие А появится не более трех раз?
Решение . Здесь p=0,4, q=0,6. Имеем:
Вероятность того, что событие А появится не больше трех раз, равна
25·0,7-0,3 ≤ m 0 ≤ 25·0,7 + 0,7, т.е. 17,2 ≤ m 0 ≤ 18,2.
Содержание практической работы
Задача 1. Монету бросают 10 раз. Найдите вероятность, что герб выпадет:
1) Вероятность выпадения герба при одном броске равна 1/2, вероятность выпадения решки также равна 1/2.
Р = С 10 4 *(1/2) 4 *(1-1/2) 10-4 = 10!/(4!*6!) * (1/2) 10 = 10*9*8*7/(2*3*4) /2 10 = 210/1024 =
2) Пусть Событие А = «Герб выпадет не менее 4-х раз».
Р(3) = С 10 3 *(1/2) 10 = 10*9*8/6 /1024 = 120/1024
Р(2) = С 10 2 *(1/2) 10 = 10*9/2 /1024 = 45/1024
Р(1) = 10*(1/2) 10 = 10/1024
Р(не А) = Р(0)+Р(1)+Р(2)+Р(3) = (120+45+10+1)/1024 = 176/1024= 0,171875
Задача 2. Игральная кость бросается 6 раз. Какова вероятность того, что шестерка выпадет 4 раза?
Вероятность выпадения шестерки равна 1/6, а не выпадения 5/6. Имеем испытания Бернулли.
Р= С 6 4* (1/4) 2 (5/6) 6-2 = 6!/(4!*2!)* 1/16 * (5/6) 4 = 15/16* 625/1296≈ 0,452
Задача 3. Вероятность изготовления нестандартной детали равна 0.11. Пользуясь формулой Бернулли найти вероятность того, что из пяти наудачу взятых деталей будут четыре стандартных.
Решение. Вероятность изготовить стандартную деталь равна 1-0,11=0,89
По формуле Бернулли
Р= С 5 4 *0,89 4 *0,11 1 = 5!/(4!*1!) *0,89 4 *0,11= 5*0,6274*0,11=0,3451
Число m называется наивероятнейшим числом наступления события А в серии из n независимых испытаний Бернулли (с вероятностью наступления события А, равной р в одном испытании) и определяется соотношением
При одном испытании вероятность наступления события А равна 3/6=1/2.
Число m называется наивероятнейшим числом наступления события А в серии из nнезависимых испытаний Бернулли (с вероятностью наступления события А, равной рв одном испытании) и определяется соотношением
Задача 6. Игральная кость бросается 16 раз. Найти наивероятнейшее число появления числа очков кратного трем.
np-q ≤ m ≤ np+p m-наивероятнейшее число наступления события А.
Задача 7. Вероятность изготовления изделия высшего сорта равна 0,87. Чему равно наиболее вероятное число изделий высшего сорта в партии из 100
Задача 8. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.
Решение. Событие А – достали белый шар. Тогда вероятности


По формуле Бернулли требуемая вероятность равна

Задача 9. Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две будут нестандартными.
Задача 10. При каждом отдельном выстреле из орудия вероятность поражения цели равна 0,9. Найти вероятность того, что из 20 выстрелов число удачных будет не менее 16 и не более 19.
Решение. Вычисляем по формуле Бернулли:
Задача 11. Что вероятнее: выиграть у равносильного противника три партии из четырех или пять партий из восьми (ничьи в отдельных партиях исключены)?
есть вероятность ровно m выигрышей в турнире из n партий. По условию задачи p = 1/2. Для такого значения p требуется сравнить вероятности P 4 (3) и P 8 (5). Имеем:
P 4 (3)
Бросание монет. Решение задач на нахождение вероятности
Кстати, сразу упомяну, что в контексте подобных задач не существенно, написать «бросают 3 монеты» или «бросают монету 3 раза», результат (в смысле вычисления вероятности) будет один и тот же (так как результаты бросков независимы друг от друга).
1. Классическое определение вероятности
Пример 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Пример 2. Дважды бросают симметричную монету. Найти вероятность того, что оба раза выпала одна сторона.
Как видим, все довольно просто. Перейдем к чуть более сложной задаче.
Пример 3. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза.
Взяли разгон и переходим к 4 монетам.
Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.
Думаю, к этому времени вы уже поняли суть метода и сможете сами решить задачи, где бросаются 2-3-4 монеты и орел не выпадает ни разу, или решка ровно один раз и т.п.
2. Комбинаторика + классическая вероятность
Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.
Конечно, этот подход кажется сложнее из-за более формального математического описания решения, но гораздо легче масштабируется.
Например, если рассмотреть подобную задачу:
Пример 5. Монету бросают 8 раз. Найти вероятность того, что герб выпадет ровно 4 раза
Ради полноты изложения приведу еще пример задачи, решаемой подобным образом (но если хотите, можете сразу переходить к более простому способу 3).
Пример 6. Монету подбрасывают 6 раз. Найти вероятность того, что гербы выпадут два раза и только подряд, а в остальные разы будут только решки.
Способ 3. Формула Бернулли
А теперь все задачи решаются проще простого, вот глядите!
Пример 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.
Пример 7. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.
Пример 8. Пусть бросают 8 монет. Найти вероятность того, что орел не менее 7 раз.
Таким образом, используя одну простейшую формулу, можно решать множество задач, причем неважно, 3 монеты бросается, или 30, сложность расчетов примерно одинакова. Но, если число бросков становится очень большим, удобнее использовать приближенные формулы Муавра-Лапласа, о которых можно узнать здесь.
Полезные ссылки
Решебник по вероятности
А здесь вы найдете более 200 задач о бросании монет с полными решениями (вводите часть текста для поиска своей задачи):
Монету бросают 10 раз какова вероятность
Кстати, сразу упомяну, что в контексте подобных задач не существенно, написать «бросают 3 монеты» или «бросают монету 3 раза», результат (в смысле вычисления вероятности) будет один и тот же (так как результаты бросков независимы друг от друга).
Для задач о подбрасывании монеты существуют два основных метода решения, один – по формуле классической вероятности (фактически переборный метод, доступный даже школьникам), а также его более сложный вариант с использованием комбинаторики, второй – по формуле Бернулли (на мой взгляд он даже легче первого, нужно только запомнить формулу). Рекомендую по порядку прочитать про оба метода, и потом выбирать при решении подходящий.
1. Классическое определение вероятности
Пример 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Пример 2. Дважды бросают симметричную монету. Найти вероятность того, что оба раза выпала одна сторона.
Как видим, все довольно просто. Перейдем к чуть более сложной задаче.
Пример 3. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза.
Взяли разгон и переходим к 4 монетам.
Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.
Думаю, к этому времени вы уже поняли суть метода и сможете сами решить задачи, где бросаются 2-3-4 монеты и орел не выпадает ни разу, или решка ровно один раз и т.п.
2. Комбинаторика + классическая вероятность
Надо заметить, что если действовать исключительно переборным методом (как это делалось выше), с ростом числа монет быстро растет число комбинаций (для 5 монет – 32, для 6 монет – 64 и так далее), так что и вероятность ошибиться при выписывании исходов велика, метод решения теряет свою простоту и привлекательность.
Один из способов решения этой проблемы – остаться в рамках формулы классической вероятности, но использовать комбинаторные методы (см. формулы комбинаторики тут) для подсчета числа исходов. Поясню на примере последней задачи, решив ее другим способом.
Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.
Конечно, этот подход кажется сложнее из-за более формального математического описания решения, но гораздо легче масштабируется.
Например, если рассмотреть подобную задачу:
Пример 5. Монету бросают 8 раз. Найти вероятность того, что герб выпадет ровно 4 раза
Ради полноты изложения приведу еще пример задачи, решаемой подобным образом (но если хотите, можете сразу переходить к более простому способу 3).
Пример 6. Монету подбрасывают 6 раз. Найти вероятность того, что гербы выпадут два раза и только подряд, а в остальные разы будут только решки.
Способ 3. Формула Бернулли
А теперь все задачи решаются проще простого, вот глядите!
Пример 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.
Пример 7. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.
Пример 8. Пусть бросают 8 монет. Найти вероятность того, что орел не менее 7 раз.
Таким образом, используя одну простейшую формулу, можно решать множество задач, причем неважно, 3 монеты бросается, или 30, сложность расчетов примерно одинакова. Но, если число бросков становится очень большим, удобнее использовать приближенные формулы Муавра-Лапласа, о которых можно узнать здесь.
Полезные ссылки
Решебник по вероятности
А здесь вы найдете более 200 задач о бросании монет с полными решениями (вводите часть текста для поиска своей задачи):
Монета брошена 10 раз. Найти вероятность того, что герб выпадет: а) от 4-х до 6-ти раз; б) хотя бы один раз.
Решение. События выпадения герба при многократном бросании монеты являются независимыми. В каждом испытании герб, так же, как и надпись, выпадает с вероятностью р = 0,5. Таким образом, задача относит-ся к схеме и формуле Бернулли. Для случая а) искомая вероятность вычисле-ния по формуле (2.4), а для случая б) – по формуле (2.3). С помощью этих формул, с учетом того, что р = 0,5 и q = 0,5 получим:
б) р10(хотя бы один раз) = 1 – q 10 = 1 – 1/1024=1023/1024.
нПОЕФХ ВТПУБАФ 10 ТБЪ. оБКДЙФЕ ЧЕТПСФОПУФШ ФПЗП, ЮФП ОЙ ТБЪХ ОЕ ЧЩРБДХФ ДЧБ ПТМБ РПДТСД.
тЕЫЕОЙЕ
рЕТЧЩК УРПУПВ. еУМЙ ПТМПЧ ОЕФ ЧПЧУЕ, ФП ФБЛБС РПУМЕДПЧБФЕМШОПУФШ УПУФПЙФ ЙЪ ДЕУСФЙ ТЕЫЕЛ Й ЧУЕЗП ПДОБ. еУМЙ ПТЕМ ПДЙО, ФП ФБЛЙИ ЛПНВЙОБГЙК 10 (ПТЕМ УФПЙФ ОБ МАВПН ЙЪ 10 НЕУФ). еУМЙ ПТМПЧ ДЧБ, ФП ЛПНВЙОБГЙК (НЩ УЮЙФБЕН ЛПМЙЮЕУФЧП ЧБТЙБОФПЧ ТБУУФБЧЙФШ 2 ПТМБ РП ПДОПНХ НЕЦДХ 8 ТЕЫЛБНЙ ЙМЙ РП ЛТБСН). й ФБЛ ДБМЕЕ. еУМЙ ПТМПЧ k, ФП ЛПНВЙОБГЙК (ЮЙУМП ЧБТЙБОФПЧ ТБУУФБЧЙФШ ПТМПЧ Ч 11 – k НЕУФ НЕЦДХ ТЕЫЛБНЙ Й РП ЛТБСН).
ъОБЮЙФ, ПВЭЕЕ ЮЙУМП ЛПНВЙОБГЙК ТБЧОП
уМЕДПЧБФЕМШОП, ЙУЛПНБС ЧЕТПСФОПУФШ ЕУФШ 144 : 2 10 = 9 /64.
пФЧЕФ
йУФПЮОЙЛЙ Й РТЕГЕДЕОФЩ ЙУРПМШЪПЧБОЙС
| ПМЙНРЙБДБ | |
| оБЪЧБОЙЕ | ъБПЮОБС ПМЙНРЙБДБ РП ФЕПТЙЙ ЧЕТПСФОПУФЕК Й УФБФЙУФЙЛЕ |
| ЗПД | |
| дБФБ | 2009 |
| ЪБДБЮБ | |
| оПНЕТ | 13 |
Методическая разработка (стр. 10 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 |

Вероятность Рn(1 £k £ n) того, что в n опытах событие А появится хотя бы один раз, определяется формулой:

Вероятность того, что в n испытаниях событие А наступит:
а) менее k раз 
б) более k раз 
в) не менее k раз 
г) не более k раз 
Задача. Вероятность попадания в мишень при одном выстреле для данного стрелка 0,7 и не зависит от номера выстрела. Найти вероятность того, что при 5 выстрелах произойдет ровно 2 попадания в мишень.
Решение. Поскольку р=0,7, то q=1-р =1-0,7=0,3. По условию n=5, k=2, по формуле (4.1.1) находим:

Решение. Обозначим через X число гербов, выпавших при этих подбрасываниях. В данном случае р=1/2 и q=1/2.
Случайная величина X может принимать следующие значения х1=0, x2=1, х3=2, х4=3, x5=4, х6=5. Поскольку Р(х> 1)=1-Р(х Р6(3), то вероятнее выиграть две партии из четырех, чем три из шести.
12. а) вероятнее выиграть одну партию из двух; б) вероятнее выиграть не менее двух партий из четырех
15. а) 0,729; б) 0,95; в) 0,99.
16. а) 0,31; б) 0,48; в) 0,52; г) 0,62.
Вопросы для самопроверки
1 Какими должны быть испытания, чтобы можно было применять формулу Бернулли?
2 Какой вид имеет формула Бернулли?
3 Как запишется закон распределения дискретной случайной величины Х-количества появившихся гербов на двух новеньких монетах? случайно оброненных на пол?
4 Какими свойствами коэффициентов бинома Ньютона можно воспользоваться для доказательства следующего утверждения: при нескольких подбрасываниях монеты вероятность выпадения герба четное число раз равно вероятности выпадения герба нечетное число раз?
5 Что называют наивероятнейшим числом появления события в n независимых испытаниях? Как находится это число?
6 Какой вид имеет формула, определяющая вероятность того, что в n независимых испытаниях событие А появится от k1 до k2 раз
7 Как найти вероятность того, что в n независимых испытаниях событие А появится хотя бы один раз?
8 Как вычислить вероятность того, что в n независимых испытаниях событие А наступит: а) менее k раз; б) более k раз; в) не менее k раз: г) не более k раз?
В данном пособии были рассмотрены основы теории вероятностей, что составляет лишь малую часть данной математической дисциплины. Но этого достаточно, чтобы познакомится с классическим определением вероятности и научиться вычислять вероятность по классической формуле.
Также приведены необходимые теоретические сведения и формулы, даны решения типовых задач и задачи для самостоятельного решения.
Методическая разработка может применяться при проведении занятий по теории вероятностей или при самостоятельном изучении основ данной дисциплины.