для чего используется регрессия в машинном обучении

Линейная регрессия

Линейная регрессия (Linear regression) — это это математическая модель, которая описывает связь нескольких переменных. Модели линейной регрессии представляют собой статистическую процедуру, помогающую прогнозировать будущее. Она применяется в научных сферах и в бизнесе, а в последние десятилетия используется в машинном обучении.

Для чего нужна линейная регрессия

Задача регрессии в машинном обучении — это предсказание одного параметра (Y) по известному параметру X, где X — набор параметров, характеризующий наблюдение.

Как работает линейная регрессия

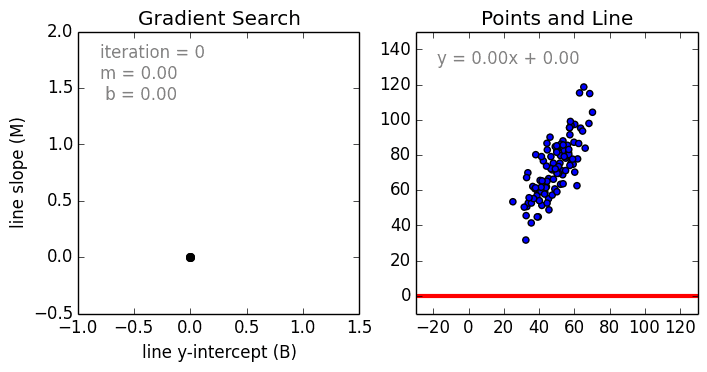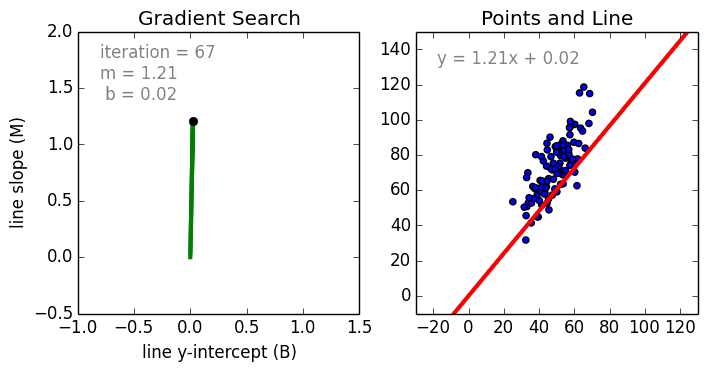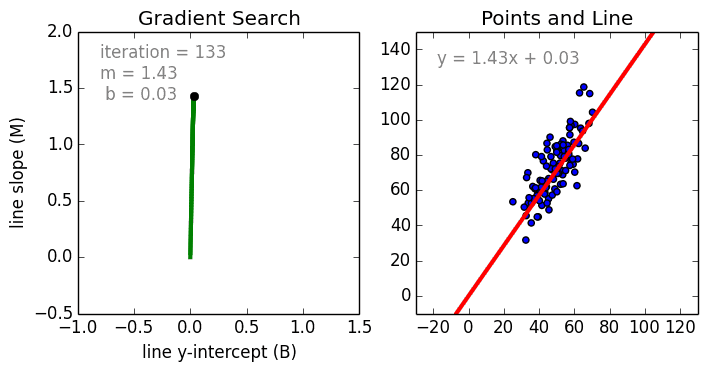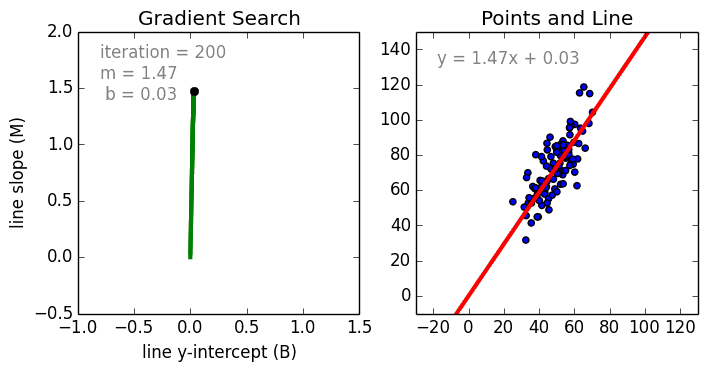
Возьмем небольшой набор данных. Предположим, что это группа коттеджей, расположенных в одном районе. На оси Х обозначена их площадь, а на оси Y — рыночная стоимость. Чтобы увидеть, как стоимость дома зависит от его площади, построим регрессию.

Это будет простая линейная регрессия с одной переменной. Изменится площадь дома — изменится и стоимость. Для вычисления используем стандартное уравнение регрессии: f (x) = b + m⋅x, где m — это наклон линии, а b — ее сдвиг по оси Y. То есть изменение коэффициентов m и b будет влиять на расположение прямой:

Провести прямую линию через все точки на графике не получится, если они расположены в хаотичном порядке. Поэтому с помощью линейной регрессии определяется оптимальный вариант расположения этой прямой. Некоторые точки все равно останутся на расстоянии, но оно должно быть минимальным. Расчет этого минимального расстояния от прямой до каждой точки называется функцией потерь.

Для оценки точности регрессии используют разные метрики, например MSE (от англ. mean squared error — средняя квадратическая ошибка). Чем ниже MSE, тем лучше модель.

В первом случае MSE будет равна 0,17, во втором — 0,08, а в третьем — 0,02. Получается, что третья прямая лучше всего показывает зависимость цены дома от его площади.

Data Scientist с нуля

Получите востребованные IT-навыки за один год и станьте перспективным профессионалом. Мы поможем в трудоустройстве. Дополнительная скидка 5% по промокоду BLOG.

Расчет линейной регрессии в Python

Построим регрессию, чтобы узнать, как кассовые сборы фильма зависят от бюджета, который вложили в его производство.

Для расчета понадобится csv-файл, который содержит информацию о бюджетах и сборах 5 034 фильмов, которые когда-то выходили в прокат. Эти данные станут базой для исследования.

Построим модель линейной регрессии с помощью Python. Для этого нужно импортировать несколько библиотек:

Модель линейной регрессии, которую нужно будет обучить, импортируется с помощью библиотеки sklearn. В качестве X будет колонка production_budget_usd, а в качестве Y – колонка worldwide_gross_usd.

На основе этих данных определяется нужный наклон прямой и расположение относительно осей координат. Это и будет нужной линейной регрессией, по которой можно предсказать сборы собственного фильма, выбрав подходящий бюджет.

В итоге получится график того, как соотносятся бюджеты и кассы у фильмов в списке. Каждая точка — это отдельная кинолента. На оси Х показаны затраты на производство, а на оси У — сколько она заработала. Теперь через эти точки нужно провести прямую так, чтобы она была максимально близка ко всем точкам на графике.

Множественная линейная регрессия

В жизни кассовые сборы кино зависят не от одной переменной, а от совокупности разных факторов: популярности жанра, режиссера, каста актеров и затрат на промокампанию. Если рассчитать все факторы, влияющие на сборы, то уравнение изменится:

Стало f(x) = b + m1*x1 + … + mn*xn

Каждый коэффициент в нем показывает важность признаков. То есть множественная регрессия демонстрирует, как каждый параметр влияет на расположение прямой, и выбирает оптимальный вариант точно так же, как и линейная — с помощью функции потерь.

Data Scientist с нуля

Получите востребованные IT-навыки за один год и станьте перспективным профессионалом. Мы поможем в трудоустройстве. Дополнительная скидка 5% по промокоду BLOG.

Источник

5 алгоритмов регрессии в машинном обучении, о которых вам следует знать

Источник: Vecteezy

Да, линейная регрессия не единственная

Быстренько назовите пять алгоритмов машинного обучения.

Вряд ли вы назовете много алгоритмов регрессии. В конце концов, единственным широко распространенным алгоритмом регрессии является линейная регрессия, главным образом из-за ее простоты. Однако линейная регрессия часто неприменима к реальным данным из-за слишком ограниченных возможностей и ограниченной свободы маневра. Ее часто используют только в качестве базовой модели для оценки и сравнения с новыми подходами в исследованиях.

Команда Mail.ru Cloud Solutions перевела статью, автор которой описывает 5 алгоритмов регрессии. Их стоит иметь в своем наборе инструментов наряду с популярными алгоритмами классификации, такими как SVM, дерево решений и нейронные сети.

1. Нейросетевая регрессия

Теория

Нейронные сети невероятно мощные, но их обычно используют для классификации. Сигналы проходят через слои нейронов и обобщаются в один из нескольких классов. Однако их можно очень быстро адаптировать в регрессионные модели, если изменить последнюю функцию активации.

Каждый нейрон передает значения из предыдущей связи через функцию активации, служащую цели обобщения и нелинейности. Обычно активационная функция — это что-то вроде сигмоиды или функции ReLU (выпрямленный линейный блок).

Источник. Свободное изображение

Но, заменив последнюю функцию активации (выходной нейрон) линейной функцией активации, выходной сигнал можно отобразить на множество значений, выходящих за пределы фиксированных классов. Таким образом, на выходе будет не вероятность отнесения входного сигнала к какому-либо одному классу, а непрерывное значение, на котором фиксирует свои наблюдения нейронная сеть. В этом смысле можно сказать, что нейронная сеть как бы дополняет линейную регрессию.

Нейросетевая регрессия имеет преимущество нелинейности (в дополнение к сложности), которую можно ввести с сигмоидной и другими нелинейными функциями активации ранее в нейронной сети. Однако чрезмерное использование ReLU в качестве функции активации может означать, что модель имеет тенденцию избегать вывода отрицательных значений, поскольку ReLU игнорирует относительные различия между отрицательными значениями.

Это можно решить либо ограничением использования ReLU и добавлением большего количества отрицательных значений соответствующих функций активации, либо нормализацией данных до строго положительного диапазона перед обучением.

Реализация

Используя Keras, построим структуру искусственной нейронной сети, хотя то же самое можно было бы сделать со сверточной нейронной сетью или другой сетью, если последний слой является либо плотным слоем с линейной активацией, либо просто слоем с линейной активацией. (Обратите внимание, что импорты Keras не указаны для экономии места).

model = Sequential()
model.add(Dense(100, input_dim=3, activation=’sigmoid’))
model.add(ReLU(alpha=1.0))
model.add(Dense(50, activation=’sigmoid’))
model.add(ReLU(alpha=1.0))
model.add(Dense(25, activation=’softmax’))

#IMPORTANT PART
model.add(Dense(1, activation=’linear’))

Проблема нейронных сетей всегда заключалась в их высокой дисперсии и склонности к переобучению. В приведенном выше примере кода много источников нелинейности, таких как SoftMax или sigmoid.

Если ваша нейронная сеть хорошо справляется с обучающими данными с чисто линейной структурой, возможно, лучше использовать регрессию с усеченным деревом решений, которая эмулирует линейную и высокодисперсную нейронную сеть, но позволяет дата-сайентисту лучше контролировать глубину, ширину и другие атрибуты для контроля переобучения.

2. Регрессия дерева решений

Теория

Деревья решений в классификации и регрессии очень похожи, поскольку работают путем построения деревьев с узлами «да/нет». Однако в то время как конечные узлы классификации приводят к одному значению класса (например, 1 или 0 для задачи бинарной классификации), деревья регрессии заканчиваются значением в непрерывном режиме (например, 4593,49 или 10,98).

Иллюстрация автора

Из-за специфической и высокодисперсной природы регрессии просто как задачи машинного обучения, регрессоры дерева решений следует тщательно обрезать. Тем не менее, подход к регрессии нерегулярен — вместо того, чтобы вычислять значение в непрерывном масштабе, он приходит к заданным конечным узлам. Если регрессор обрезан слишком сильно, у него слишком мало конечных узлов, чтобы должным образом выполнить свою задачу.

Следовательно, дерево решений должно быть обрезано так, чтобы оно имело наибольшую свободу (возможные выходные значения регрессии — количество конечных узлов), но недостаточно, чтобы оно было слишком глубоким. Если его не обрезать, то и без того высокодисперсный алгоритм станет чрезмерно сложным из-за природы регрессии.

Реализация

Регрессия дерева решений может быть легко создана в sklearn :

Бонус: близкий родственник дерева решений, алгоритм random forest (алгоритм случайного леса), также может быть реализован в качестве регрессора. Регрессор случайного леса может работать лучше или не лучше, чем дерево решений в регрессии (в то время как он обычно работает лучше в классификации) из-за тонкого баланса между избыточным и недостаточным в природе алгоритмов построения дерева.

3. Регрессия LASSO

Метод регрессии лассо (LASSO, Least Absolute Shrinkage and Selection Operator) — это вариация линейной регрессии, специально адаптированная для данных, которые демонстрируют сильную мультиколлинеарность (то есть сильную корреляцию признаков друг с другом).

Она автоматизирует части выбора модели, такие как выбор переменных или исключение параметров. LASSO использует сжатие коэффициентов (shrinkage), то есть процесс, в котором значения данных приближаются к центральной точке (например среднему значению).

Иллюстрация автора. Упрощенная визуализация процесса сжатия

Процесс сжатия добавляет регрессионным моделям несколько преимуществ:

Регрессия лассо использует регуляризацию L1, то есть взвешивает ошибки по их абсолютному значению. Вместо, например, регуляризации L2, которая взвешивает ошибки по их квадрату, чтобы сильнее наказывать за более значительные ошибки.

Такая регуляризация часто приводит к более разреженным моделям с меньшим количеством коэффициентов, так как некоторые коэффициенты могут стать нулевыми и, следовательно, будут исключены из модели. Это позволяет ее интерпретировать.

Реализация

В sklearn регрессия лассо поставляется с моделью перекрестной проверки, которая выбирает наиболее эффективные из многих обученных моделей с различными фундаментальными параметрами и путями обучения, что автоматизирует задачу, которую иначе пришлось бы выполнять вручную.

4. Гребневая регрессия (ридж-регрессия)

Теория

Гребневая регрессия или ридж-регрессия очень похожа на регрессию LASSO в том, что она применяет сжатие. Оба алгоритма хорошо подходят для наборов данных с большим количеством признаков, которые не являются независимыми друг от друга (коллинеарность).

Однако самое большое различие между ними в том, что гребневая регрессия использует регуляризацию L2, то есть ни один из коэффициентов не становится нулевым, как это происходит в регрессии LASSO. Вместо этого коэффициенты всё больше приближаются к нулю, но не имеют большого стимула достичь его из-за природы регуляризации L2.

Сравнение ошибок в регрессии лассо (слева) и гребневой регрессии (справа). Поскольку гребневая регрессия использует регуляризацию L2, ее площадь напоминает круг, тогда как регуляризация лассо L1 рисует прямые линии. Свободное изображение. Источник

В лассо улучшение от ошибки 5 до ошибки 4 взвешивается так же, как улучшение от 4 до 3, а также от 3 до 2, от 2 до 1 и от 1 до 0. Следовательно, больше коэффициентов достигает нуля и устраняется больше признаков.

Однако в гребневой регрессии улучшение от ошибки 5 до ошибки 4 вычисляется как 5² − 4² = 9, тогда как улучшение от 4 до 3 взвешивается только как 7. Постепенно вознаграждение за улучшение уменьшается; следовательно, устраняется меньше признаков.

Гребневая регрессия лучше подходит в ситуации, когда мы хотим сделать приоритетными большое количество переменных, каждая из которых имеет небольшой эффект. Если в модели требуется учитывать несколько переменных, каждая из которых имеет средний или большой эффект, лучшим выбором будет лассо.

Реализация

Гребневую регрессию в sklearn можно реализовать следующим образом (см. ниже). Как и для регрессии лассо, в sklearn есть реализация для перекрестной проверки выбора лучших из многих обученных моделей.

5. Регрессия ElasticNet

Теория

ElasticNet стремится объединить лучшее из гребневой регрессии и регрессии лассо, комбинируя регуляризацию L1 и L2.

Лассо и гребневая регрессия представляют собой два различных метода регуляризации. В обоих случаях λ — это ключевой фактор, который контролирует размер штрафа:

Источник

Регрессия в машинном обучении: оптимальный алгоритм

Регрессия используется в ML. Рассмотрим несколько алгоритмов и определим, как их использовать, исходя из преимуществ и недостатков.

Сталкиваясь с какой-либо проблемой в ML, помните, что есть множество алгоритмов, позволяющих её решить. Однако не существует такого универсального алгоритма, который подходил бы под все случаи и решал абсолютно все проблемы.

Выбор алгоритма строго зависит от размера и структуры ваших данных. Таким образом, выбор правильного алгоритма может быть неясен до тех пор, пока мы не проверим возможные варианты и не наткнёмся на ошибки.

Но каждый алгоритм обладает как преимуществами, так и недостатками, которые можно использовать в качестве руководства для выбора наиболее подходящего под ситуацию.

Линейная и полиномиальная регрессия

Начнём с простого. Одномерная (простая) линейная регрессия – это метод, используемый для моделирования отношений между одной независимой входной переменной (переменной функции) и выходной зависимой переменной. Модель линейная.

Более общий случай – множественная линейная регрессия, где создаётся модель взаимосвязи между несколькими входными переменными и выходной зависимой переменной. Модель остаётся линейной, поскольку выходное значение представляет собой линейную комбинацию входных значений.

Также стоит упомянуть полиномиальную регрессию. Модель становится нелинейной комбинацией входных переменных, т. е. среди них могут быть экспоненциальные переменные: синус, косинус и т. п. Модели регрессии можно обучить с помощью метода стохастического градиента.

Преимущества:

Недостатки:

Нейронные сети

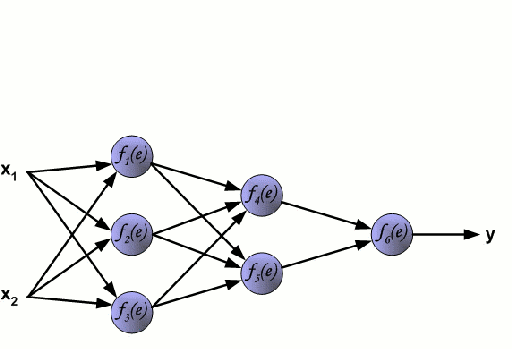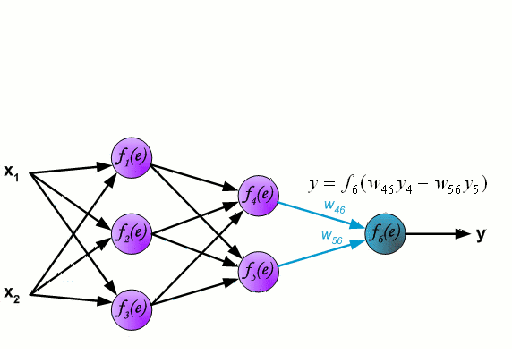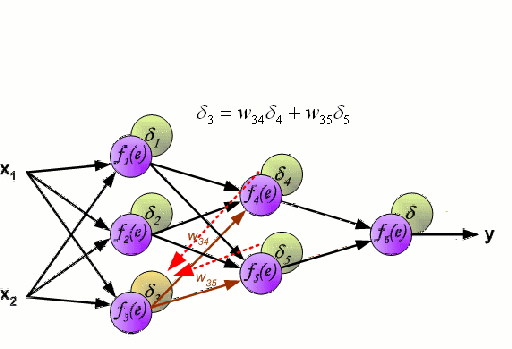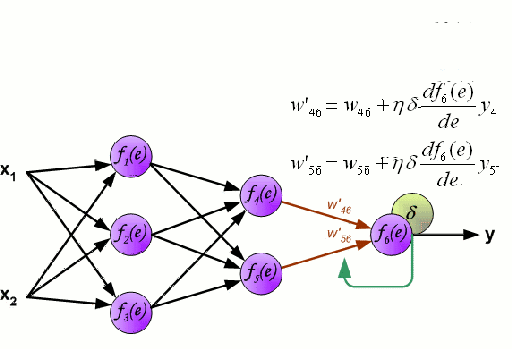
Нейронная сеть состоит из взаимосвязанных групп узлов, называемых нейронами. Входные данные передаются в эти нейроны в виде линейной комбинации со множеством переменных. Значение, умножаемое на каждую функциональную переменную, называется весом. Затем к этой линейной комбинации применяется нелинейность, что даёт нейронной сети возможность моделировать сложные нелинейные отношения. Чаще всего нейросети бывают многослойными: выход одного слоя передается следующему так, как описано выше. На выходе нелинейность не применяется.

Нейронные сети тренируются с помощью метода стохастического градиента и алгоритма обратного распространения ошибки.

Преимущества:

Недостатки:

Дерево принятия решений и Случайный лес

Начнём с простого случая. Дерево принятия решений – это представления правил, находящихся в последовательной, иерархической структуре, где каждому объекту соответствует узел, дающий решение. При построении дерева важно классифицировать атрибуты так, чтобы создать “чистые” узлы. То есть выбранный атрибут должен разбить множество так, чтобы получаемые в итоге подмножества состояли из объектов, принадлежащих к одному классу, или были максимально приближены к этому, т.е. количество объектов из других классов в каждом из этих множеств было как можно меньше.

“Случайные лес” – совокупность деревьев принятия решений. Входной вектор проходит через несколько деревьев решений. Для регрессии выходное значение всех деревьев усредняется; для классификации используется схема голосования для определения конечного класса.

Источник

Открытый курс машинного обучения. Тема 4. Линейные модели классификации и регрессии

Сегодня мы детально обсудим очень важный класс моделей машинного обучения – линейных. Ключевое отличие нашей подачи материала от аналогичной в курсах эконометрики и статистики – это акцент на практическом применении линейных моделей в реальных задачах (хотя и математики тоже будет немало).

Пример такой задачи – это соревнование Kaggle Inclass по идентификации пользователя в Интернете по его последовательности переходов по сайтам.

UPD: теперь курс — на английском языке под брендом mlcourse.ai со статьями на Medium, а материалами — на Kaggle (Dataset) и на GitHub.

Все материалы доступны на GitHub.
А вот видеозапись лекции по мотивам этой статьи в рамках второго запуска открытого курса (сентябрь-ноябрь 2017). В ней, в частности, рассмотрены два бенчмарка соревнования, полученные с помощью логистической регрессии.

1. Линейная регрессия

Метод наименьших квадратов

Рассказ про линейные модели мы начнем с линейной регрессии. В первую очередь, необходимо задать модель зависимости объясняемой переменной от объясняющих ее факторов, функция зависимости будет линейной: . Если мы добавим фиктивную размерность для каждого наблюдения, тогда линейную форму можно переписать чуть более компактно, записав свободный член под сумму: . Если рассматривать матрицу наблюдения-признаки, у которой в строках находятся примеры из набора данных, то нам необходимо добавить единичную колонку слева. Зададим модель следующим образом:

Можем выписать выражение для каждого конкретного наблюдения

Также на модель накладываются следующие ограничения (иначе это будет какая то другая регрессия, но точно не линейная):

Оценка весов называется линейной, если

где зависит только от наблюдаемых данных и почти наверняка нелинейно. Так как решением задачи поиска оптимальных весов будет именно линейная оценка, то и модель называется линейной регрессией. Введем еще одно определение. Оценка называется несмещенной тогда, когда матожидание оценки равно реальному, но неизвестному значению оцениваемого параметра:

Один из способов вычислить значения параметров модели является метод наименьших квадратов (МНК), который минимизирует среднеквадратичную ошибку между реальным значением зависимой переменной и прогнозом, выданным моделью:

Для решения данной оптимизационной задачи необходимо вычислить производные по параметрам модели, приравнять их к нулю и решить полученные уравнения относительно (матричное дифференцирование неподготовленному читателю может показаться затруднительным, попробуйте расписать все через суммы, чтобы убедиться в ответе):

Итак, имея в виду все определения и условия описанные выше, мы можем утверждать, опираясь на теорему Маркова-Гаусса, что оценка МНК является лучшей оценкой параметров модели, среди всех линейных и несмещенных оценок, то есть обладающей наименьшей дисперсией.

Метод максимального правдоподобия

У читателя вполне резонно могли возникнуть вопросы: например, почему мы минимизируем среднеквадратичную ошибку, а не что-то другое. Ведь можно минимизировать среднее абсолютное значение невязки или еще что-то. Единственное, что произойдёт в случае изменения минимизируемого значения, так это то, что мы выйдем из условий теоремы Маркова-Гаусса, и наши оценки перестанут быть лучшими среди линейных и несмещенных.

Давайте перед тем как продолжить, сделаем лирическое отступление, чтобы проиллюстрировать метод максимального правдоподобия на простом примере.

Как-то после школы я заметил, что все помнят формулу этилового спирта. Тогда я решил провести эксперимент: помнят ли люди более простую формулу метилового спирта: . Мы опросили 400 человек и оказалось, что формулу помнят всего 117 человек. Разумно предположить, что вероятность того, что следующий опрошенный знает формулу метилового спирта – . Покажем, что такая интуитивно понятная оценка не просто хороша, а еще и является оценкой максимального правдоподобия.

Разберемся, откуда берется эта оценка, а для этого вспомним определение распределения Бернулли: случайная величина имеет распределение Бернулли, если она принимает всего два значения ( и с вероятностями и соответственно) и имеет следующую функцию распределения вероятности:

Похоже, это распределение – то, что нам нужно, а параметр распределения и есть та оценка вероятности того, что человек знает формулу метилового спирта. Мы проделали независимых экспериментов, обозначим их исходы как . Запишем правдоподобие наших данных (наблюдений), то есть вероятность наблюдать 117 реализаций случайной величины и 283 реализации :

Далее будем максимизировать это выражение по , и чаще всего это делают не с правдоподобием , а с его логарифмом (применение монотонного преобразования не изменит решение, но упростит вычисления):

Теперь мы хотим найти такое значение , которое максимизирует правдоподобие, для этого мы возьмем производную по , приравняем к нулю и решим полученное уравнение:

Получается, что наша интуитивная оценка – это и есть оценка максимального правдоподобия. Применим теперь те же рассуждения для задачи линейной регрессии и попробуем выяснить, что лежит за среднеквадратичной ошибкой. Для этого нам придется посмотреть на линейную регрессию с вероятностной точки зрения. Модель, естественно, остается такой же:

но будем теперь считать, что случайные ошибки берутся из центрированного нормального распределения:

Перепишем модель в новом свете:

Так как примеры берутся независимо (ошибки не скоррелированы – одно из условий теоремы Маркова-Гаусса), то полное правдоподобие данных будет выглядеть как произведение функций плотности . Рассмотрим логарифм правдоподобия, что позволит нам перейти от произведения к сумме:

Мы хотим найти гипотезу максимального правдоподобия, т.е. нам нужно максимизировать выражение , а это то же самое, что и максимизация его логарифма. Обратите внимание, что при максимизации функции по какому-то параметру можно выкинуть все члены, не зависящие от этого параметра:

Таким образом, мы увидели, что максимизация правдоподобия данных – это то же самое, что и минимизация среднеквадратичной ошибки (при справедливости указанных выше предположений). Получается, что именно такая функция стоимости является следствием того, что ошибка распределена нормально, а не как-то по-другому.

Разложение ошибки на смещение и разброс (Bias-variance decomposition)

Поговорим немного о свойствах ошибки прогноза линейной регрессии (в принципе эти рассуждения верны для всех алгоритмов машинного обучения). В свете предыдущего пункта мы выяснили, что:

Тогда ошибка в точке раскладывается следующим образом:

Для наглядности опустим обозначение аргумента функций. Рассмотрим каждый член в отдельности, первые два расписываются легко по формуле :

И теперь последний член суммы. Мы помним, что ошибка и целевая переменная независимы друг от друга:

Наконец, собираем все вместе:

Итак, мы достигли цели всех вычислений, описанных выше, последняя формула говорит нам, что ошибка прогноза любой модели вида складывается из:

Если с последней мы ничего сделать не можем, то на первые два слагаемых мы можем как-то влиять. В идеале, конечно же, хотелось бы свести на нет оба этих слагаемых (левый верхний квадрат рисунка), но на практике часто приходится балансировать между смещенными и нестабильными оценками (высокая дисперсия).

Как правило, при увеличении сложности модели (например, при увеличении количества свободных параметров) увеличивается дисперсия (разброс) оценки, но уменьшается смещение. Из-за того что тренировочный набор данных полностью запоминается вместо обобщения, небольшие изменения приводят к неожиданным результатам (переобучение). Если же модель слабая, то она не в состоянии выучить закономерность, в результате выучивается что-то другое, смещенное относительно правильного решения.

Теорема Маркова-Гаусса как раз утверждает, что МНК-оценка параметров линейной модели является самой лучшей в классе несмещенных линейных оценок, то есть с наименьшей дисперсией. Это значит, что если существует какая-либо другая несмещенная модель тоже из класса линейных моделей, то мы можем быть уверены, что .

Регуляризация линейной регрессии

Иногда бывают ситуации, когда мы намеренно увеличиваем смещенность модели ради ее стабильности, т.е. ради уменьшения дисперсии модели . Одним из условий теоремы Маркова-Гаусса является полный столбцовый ранг матрицы . В противном случае решение МНК не существует, т.к. не будет существовать обратная матрица Другими словами, матрица будет сингулярна, или вырожденна. Такая задача называется некорректно поставленной. Задачу нужно скорректировать, а именно, сделать матрицу невырожденной, или регулярной (именно поэтому этот процесс называется регуляризацией). Чаще в данных мы можем наблюдать так называемую мультиколлинеарность — когда два или несколько признаков сильно коррелированы, в матрице это проявляется в виде «почти» линейной зависимости столбцов. Например, в задаче прогнозирования цены квартиры по ее параметрам «почти» линейная зависимость будет у признаков «площадь с учетом балкона» и «площадь без учета балкона». Формально для таких данных матрица будет обратима, но из-за мультиколлинеарности у матрицы некоторые собственные значения будут близки к нулю, а в обратной матрице появятся экстремально большие собственные значения, т.к. собственные значения обратной матрицы – это . Итогом такого шатания собственных значений станет нестабильная оценка параметров модели, т.е. добавление нового наблюдения в набор тренировочных данных приведёт к совершенно другому решению. Иллюстрации роста коэффициентов вы найдете в одном из наших прошлых постов. Одним из способов регуляризации является регуляризация Тихонова, которая в общем виде выглядит как добавление нового члена к среднеквадратичной ошибке:

Часто матрица Тихонова выражается как произведение некоторого числа на единичную матрицу: . В этом случае задача минимизации среднеквадратичной ошибки становится задачей с ограничением на норму. Если продифференцировать новую функцию стоимости по параметрам модели, приравнять полученную функцию к нулю и выразить , то мы получим точное решение задачи.

Такая регрессия называется гребневой регрессией (ridge regression). А гребнем является как раз диагональная матрица, которую мы прибавляем к матрице , в результате получается гарантированно регулярная матрица.

Такое решение уменьшает дисперсию, но становится смещенным, т.к. минимизируется также и норма вектора параметров, что заставляет решение сдвигаться в сторону нуля. На рисунке ниже на пересечении белых пунктирных линий находится МНК-решение. Голубыми точками обозначены различные решения гребневой регрессии. Видно, что при увеличении параметра регуляризации решение сдвигается в сторону нуля.

Советуем обратиться в наш прошлый пост за примером того, как регуляризация справляется с проблемой мультиколлинеарности, а также чтобы освежить в памяти еще несколько интерпретаций регуляризации.

2. Логистическая регрессия

Линейный классификатор

Основная идея линейного классификатора заключается в том, что признаковое пространство может быть разделено гиперплоскостью на два полупространства, в каждом из которых прогнозируется одно из двух значений целевого класса.
Если это можно сделать без ошибок, то обучающая выборка называется линейно разделимой.

Мы уже знакомы с линейной регрессией и методом наименьших квадратов. Рассмотрим задачу бинарной классификации, причем метки целевого класса обозначим «+1» (положительные примеры) и «-1» (отрицательные примеры).
Один из самых простых линейных классификаторов получается на основе регрессии вот таким образом:

Логистическая регрессия как линейный классификатор

Логистическая регрессия является частным случаем линейного классификатора, но она обладает хорошим «умением» – прогнозировать вероятность отнесения примера к классу «+»:

Прогнозирование не просто ответа («+1» или «-1»), а именно вероятности отнесения к классу «+1» во многих задачах является очень важным бизнес-требованием. Например, в задаче кредитного скоринга, где традиционно применяется логистическая регрессия, часто прогнозируют вероятность невозврата кредита (). Клиентов, обратившихся за кредитом, сортируют по этой предсказанной вероятности (по убыванию), и получается скоркарта — по сути, рейтинг клиентов от плохих к хорошим. Ниже приведен игрушечный пример такой скоркарты.

Банк выбирает для себя порог предсказанной вероятности невозврата кредита (на картинке – ) и начиная с этого значения уже не выдает кредит. Более того, можно умножить предсказанную вероятность на выданную сумму и получить матожидание потерь с клиента, что тоже будет хорошей бизнес-метрикой (Далее в комментариях специалисты по скорингу могут поправить, но главная суть примерно такая).

Итак, мы хотим прогнозировать вероятность , а пока умеем строить линейный прогноз с помощью МНК: . Каким образом преобразовать полученное значение в вероятность, пределы которой – [0, 1]? Очевидно, для этого нужна некоторая функция В модели логистической регрессии для этого берется конкретная функция: . И сейчас разберемся, каковы для этого предпосылки.

Обозначим вероятностью происходящего события . Тогда отношение вероятностей определяется из , а это — отношение вероятностей того, произойдет ли событие или не произойдет. Очевидно, что вероятность и отношение шансов содержат одинаковую информацию. Но в то время как находится в пределах от 0 до 1, находится в пределах от 0 до .

Если вычислить логарифм (то есть называется логарифм шансов, или логарифм отношения вероятностей), то легко заметить, что . Его-то мы и будем прогнозировать с помощью МНК.

Посмотрим, как логистическая регрессия будет делать прогноз (пока считаем, что веса мы как-то получили (т.е. обучили модель), далее разберемся, как именно).

Шаг 1. Вычислить значение . (уравнение задает гиперплоскость, разделяющую примеры на 2 класса);

Шаг 2. Вычислить логарифм отношения шансов: .

Шаг 3. Имея прогноз шансов на отнесение к классу «+» – , вычислить с помощью простой зависимости:

В правой части мы получили как раз сигмоид-функцию.

Итак, логистическая регрессия прогнозирует вероятность отнесения примера к классу «+» (при условии, что мы знаем его признаки и веса модели) как сигмоид-преобразование линейной комбинации вектора весов модели и вектора признаков примера:

Следующий вопрос: как модель обучается? Тут мы опять обращаемся к принципу максимального правдоподобия.

Принцип максимального правдоподобия и логистическая регрессия

Теперь посмотрим, как из принципа максимального правдоподобия получается оптимизационная задача, которую решает логистическая регрессия, а именно, – минимизация логистической функции потерь.
Только что мы увидели, что логистическая регрессия моделирует вероятность отнесения примера к классу «+» как

Тогда для класса «-» аналогичная вероятность:

Оба этих выражения можно ловко объединить в одно (следите за моими руками – не обманывают ли вас):

Выражение называется отступом (margin) классификации на объекте (не путать с зазором (тоже margin), про который чаще всего говорят в контексте SVM). Если он неотрицателен, модель не ошибается на объекте , если же отрицателен – значит, класс для спрогнозирован неправильно.
Заметим, что отступ определен для объектов именно обучающей выборки, для которых известны реальные метки целевого класса .

Чтобы понять, почему это мы сделали такие выводы, обратимся к геометрической интерпретации линейного классификатора. Подробно про это можно почитать в материалах Евгения Соколова.

Рекомендую решить почти классическую задачу из начального курса линейной алгебры: найти расстояние от точки с радиус-вектором до плоскости, которая задается уравнением

Когда получим (или посмотрим) ответ, то поймем, что чем больше по модулю выражение , тем дальше точка находится от плоскости

Значит, выражение – это своего рода «уверенность» модели в классификации объекта :

Теперь распишем правдоподобие выборки, а именно, вероятность наблюдать данный вектор у выборки . Делаем сильное предположение: объекты приходят независимо, из одного распределения (i.i.d.). Тогда

где – длина выборки (число строк).

Как водится, возьмем логарифм данного выражения (сумму оптимизировать намного проще, чем произведение):

То есть в даном случае принцип максимизации правдоподобия приводит к минимизации выражения

Это логистическая функция потерь, просуммированная по всем объектам обучающей выборки.

Посмотрим на новую фунцию как на функцию от отступа: . Нарисуем ее график, а также график 1/0 функциий потерь (zero-one loss), которая просто штрафует модель на 1 за ошибку на каждом объекте (отступ отрицательный): .

Картинка отражает общую идею, что в задаче классификации, не умея напрямую минимизировать число ошибок (по крайней мере, градиентными методами это не сделать – производная 1/0 функциий потерь в нуле обращается в бесконечность), мы минимизируем некоторую ее верхнюю оценку. В данном случае это логистическая функция потерь (где логарифм двоичный, но это не принципиально), и справедливо

где – попросту число ошибок логистической регрессии с весами на выборке .

То есть уменьшая верхнюю оценку на число ошибок классификации, мы таким образом надеемся уменьшить и само число ошибок.

-регуляризация логистических потерь

L2-регуляризация логистической регрессии устроена почти так же, как и в случае с гребневой (Ridge регрессией). Вместо функционала минимизируется следующий:

В случае логистической регрессии принято введение обратного коэффициента регуляризации . И тогда решением задачи будет

Далее рассмотрим пример, позволяющий интуитивно понять один из смыслов регуляризации.

3. Наглядный пример регуляризации логистической регрессии

В 1 статье уже приводился пример того, как полиномиальные признаки позволяют линейным моделям строить нелинейные разделяющие поверхности. Покажем это в картинках.

Посмотрим, как регуляризация влияет на качество классификации на наборе данных по тестированию микрочипов из курса Andrew Ng по машинному обучению.
Будем использовать логистическую регрессию с полиномиальными признаками и варьировать параметр регуляризации C.
Сначала посмотрим, как регуляризация влияет на разделяющую границу классификатора, интуитивно распознаем переобучение и недообучение.
Потом численно установим близкий к оптимальному параметр регуляризации с помощью кросс-валидации (cross-validation) и перебора по сетке (GridSearch).

Загружаем данные с помощью метода read_csv библиотеки pandas. В этом наборе данных для 118 микрочипов (объекты) указаны результаты двух тестов по контролю качества (два числовых признака) и сказано, пустили ли микрочип в производство. Признаки уже центрированы, то есть из всех значений вычтены средние по столбцам. Таким образом, «среднему» микрочипу соответствуют нулевые значения результатов тестов.

RangeIndex: 118 entries, 0 to 117
Data columns (total 3 columns):
test1 118 non-null float64
test2 118 non-null float64
released 118 non-null int64
dtypes: float64(2), int64(1)
memory usage: 2.8 KB

Посмотрим на первые и последние 5 строк.

Сохраним обучающую выборку и метки целевого класса в отдельных массивах NumPy. Отобразим данные. Красный цвет соответствует бракованным чипам, зеленый – нормальным.

Определяем функцию для отображения разделяющей кривой классификатора

Полиномиальными признаками до степени для двух переменных и мы называем следующие:

Например, для это будут следующие признаки:

Нарисовав треугольник Пифагора, Вы сообразите, сколько таких признаков будет для и вообще для любого .
Попросту говоря, таких признаков экспоненциально много, и строить, скажем, для 100 признаков полиномиальные степени 10 может оказаться затратно (а более того, и не нужно).

Создадим объект sklearn, который добавит в матрицу полиномиальные признаки вплоть до степени 7 и обучим логистическую регрессию с параметром регуляризации . Изобразим разделяющую границу.
Также проверим долю правильных ответов классификатора на обучающей выборке. Видим, что регуляризация оказалась слишком сильной, и модель «недообучилась». Доля правильных ответов классификатора на обучающей выборке оказалась равной 0.627.

Увеличим до 1. Тем самым мы ослабляем регуляризацию, теперь в решении значения весов логистической регрессии могут оказаться больше (по модулю), чем в прошлом случае. Теперь доля правильных ответов классификатора на обучающей выборке – 0.831.

Еще увеличим – до 10 тысяч. Теперь регуляризации явно недостаточно, и мы наблюдаем переобучение. Можно заметить, что в прошлом случае (при =1 и «гладкой» границе) доля правильных ответов модели на обучающей выборке не намного ниже, чем в 3 случае, зато на новой выборке, можно себе представить, 2 модель сработает намного лучше.
Доля правильных ответов классификатора на обучающей выборке – 0.873.

Чтоб обсудить результаты, перепишем формулу для функционала, который оптимизируется в логистической регрессии, в таком виде:

Промежуточные выводы:

Настройка параметра регуляризации

Теперь найдем оптимальное (в данном примере) значение параметра регуляризации . Сделать это можно с помощью LogisticRegressionCV – перебора параметров по сетке с последующей кросс-валидацией. Этот класс создан специально для логистической регрессии (для нее известны эффективные алгоритмы перебора параметров), для произвольной модели мы бы использовали GridSearchCV, RandomizedSearchCV или, например, специальные алгоритмы оптимизации гиперпараметров, реализованные в hyperopt.

Посмотрим, как качество модели (доля правильных ответов на обучающей и валидационной выборках) меняется при изменении гиперпараметра .

Выделим участок с «лучшими» значениями C.

Как мы помним, такие кривые называются валидационными, раньше мы их строили вручную, но в sklearn для них их построения есть специальные методы, которые мы тоже сейчас будем использовать.

4. Где логистическая регрессия хороша и где не очень

Анализ отзывов IMDB к фильмам

Будем решать задачу бинарной классификации отзывов IMDB к фильмам. Имеется обучающая выборка с размеченными отзывами, по 12500 отзывов известно, что они хорошие, еще про 12500 – что они плохие. Здесь уже не так просто сразу приступить к машинному обучению, потому что готовой матрицы нет – ее надо приготовить. Будем использовать самый простой подход – мешок слов («Bag of words»). При таком подходе признаками отзыва будут индикаторы наличия в нем каждого слова из всего корпуса, где корпус – это множество всех отзывов. Идея иллюстрируется картинкой

Загрузим данные отсюда (краткое описание — тут). В обучающей и тестовой выборках по 12500 тысяч хороших и плохих отзывов к фильмам.

Пример плохого отзыва:

‘Words can\’t describe how bad this movie is. I can\’t explain it by writing only. You have too see it for yourself to get at grip of how horrible a movie really can be. Not that I recommend you to do that. There are so many clich\xc3\xa9s, mistakes (and all other negative things you can imagine) here that will just make you cry. To start with the technical first, there are a LOT of mistakes regarding the airplane. I won\’t list them here, but just mention the coloring of the plane. They didn\’t even manage to show an airliner in the colors of a fictional airline, but instead used a 747 painted in the original Boeing livery. Very bad. The plot is stupid and has been done many times before, only much, much better. There are so many ridiculous moments here that i lost count of it really early. Also, I was on the bad guys\’ side all the time in the movie, because the good guys were so stupid. «Executive Decision» should without a doubt be you\’re choice over this one, even the «Turbulence»-movies are better. In fact, every other movie in the world is better than this one.’

Пример хорошего отзыва:

Простой подсчет слов

Составим словарь всех слов с помощью CountVectorizer. Всего в выборке 74849 уникальных слов. Если посмотреть на примеры полученных «слов» (лучше их называть токенами), то можно увидеть, что многие важные этапы обработки текста мы тут пропустили (автоматическая обработка текстов – это могло бы быть темой отдельной серии статей).

[’00’, ‘000’, ‘0000000000001’, ‘00001’, ‘00015’, ‘000s’, ‘001’, ‘003830’, ‘006’, ‘007’, ‘0079’, ‘0080’, ‘0083’, ‘0093638’, ’00am’, ’00pm’, ’00s’, ’01’, ’01pm’, ’02’, ‘020410’, ‘029’, ’03’, ’04’, ‘041’, ’05’, ‘050’, ’06’, ’06th’, ’07’, ’08’, ‘087’, ‘089’, ’08th’, ’09’, ‘0f’, ‘0ne’, ‘0r’, ‘0s’, ’10’, ‘100’, ‘1000’, ‘1000000’, ‘10000000000000’, ‘1000lb’, ‘1000s’, ‘1001’, ‘100b’, ‘100k’, ‘100m’]
[‘pincher’, ‘pinchers’, ‘pinches’, ‘pinching’, ‘pinchot’, ‘pinciotti’, ‘pine’, ‘pineal’, ‘pineapple’, ‘pineapples’, ‘pines’, ‘pinet’, ‘pinetrees’, ‘pineyro’, ‘pinfall’, ‘pinfold’, ‘ping’, ‘pingo’, ‘pinhead’, ‘pinheads’, ‘pinho’, ‘pining’, ‘pinjar’, ‘pink’, ‘pinkerton’, ‘pinkett’, ‘pinkie’, ‘pinkins’, ‘pinkish’, ‘pinko’, ‘pinks’, ‘pinku’, ‘pinkus’, ‘pinky’, ‘pinnacle’, ‘pinnacles’, ‘pinned’, ‘pinning’, ‘pinnings’, ‘pinnochio’, ‘pinnocioesque’, ‘pino’, ‘pinocchio’, ‘pinochet’, ‘pinochets’, ‘pinoy’, ‘pinpoint’, ‘pinpoints’, ‘pins’, ‘pinsent’]

Закодируем предложения из текстов обучающей выборки индексами входящих слов. Используем разреженный формат. Преобразуем так же тестовую выборку.

Обучим логистическую регрессию и посмотрим на доли правильных ответов на обучающей и тестовой выборках. Получается, на тестовой выборке мы правильно угадываем тональность примерно 86.7% отзывов.

Коэффициенты модели можно красиво отобразить.

Подберем коэффициент регуляризации для логистической регрессии. Используем sklearn.pipeline, поскольку CountVectorizer правильно применять только на тех данных, на которых в текущий момент обучается модель (чтоб не «подсматривать» в тестовую выборку и не считать по ней частоты вхождения слов). В данном случае pipeline задает последовательность действий: применить CountVectorizer, затем обучить логистическую регрессию. Так мы поднимаем долю правильных ответов до 88.5% на кросс-валидации и 87.9% – на отложенной выборке.

Теперь то же самое, но со случайным лесом. Видим, что с логистической регрессией мы достигаем большей доли правильных ответов меньшими усилиями. Лес работает дольше, на отложенной выборке 85.5% правильных ответов.

XOR-проблема

Теперь рассмотрим пример, где линейные модели справляются хуже.

Линейные методы классификации строят все же очень простую разделяющую поверхность – гиперплоскость. Самый известный игрушечный пример, в котором классы нельзя без ошибок поделить гиперплоскостью (то есть прямой, если это 2D), получил имя «the XOR problem».

XOR – это «исключающее ИЛИ», булева функция со следующей таблицей истинности:

XOR дал имя простой задаче бинарной классификации, в которой классы представлены вытянутыми по диагоналям и пересекающимися облаками точек.

Очевидно, нельзя провести прямую так, чтобы без ошибок отделить один класс от другого. Поэтому логистическая регрессия плохо справляется с такой задачей.

А вот если на вход подать полиномиальные признаки, в данном случае до 2 степени, то проблема решается.

Здесь логистическая регрессия все равно строила гиперплоскость, но в 6-мерном пространстве признаков и . В проекции на исходное пространство признаков граница получилась нелинейной.

На практике полиномиальные признаки действительно помогают, но строить их явно – вычислительно неэффективно. Гораздо быстрее работает SVM с ядровым трюком. При таком подходе в пространстве высокой размерности считается только расстояние между объектами (задаваемое функцией-ядром), а явно плодить комбинаторно большое число признаков не приходится. Про это подробно можно почитать в курсе Евгения Соколова (математика уже серьезная).

5. Кривые валидации и обучения

Мы уже получили представление о проверке модели, кросс-валидации и регуляризации.
Теперь рассмотрим главный вопрос:

Если качество модели нас не устраивает, что делать?

Ответы на данные вопросы не всегда лежат на поверхности. В частности, иногда использование более сложной модели приведет к ухудшению показателей. Либо добавление наблюдений не приведет к ощутимым изменениям. Способность принять правильное решение и выбрать правильный способ улучшения модели, собственно говоря, и отличает хорошего специалиста от плохого.

Будем работать со знакомыми данными по оттоку клиентов телеком-оператора.

Логистическую регрессию будем обучать стохастическим градиентным спуском. Пока объясним это тем, что так быстрее, но далее в программе у нас отдельная статья про это дело. Построим валидационные кривые, показывающие, как качество (ROC AUC) на обучающей и проверочной выборке меняется с изменением параметра регуляризации.

Тенденция видна сразу, и она очень часто встречается.

Для простых моделей тренировочная и валидационная ошибка находятся где-то рядом, и они велики. Это говорит о том, что модель недообучилась: то есть она не имеет достаточное кол-во параметров.

Для сильно усложненных моделей тренировочная и валидационная ошибки значительно отличаются. Это можно объяснить переобучением: когда параметров слишком много либо не хватает регуляризации, алгоритм может «отвлекаться» на шум в данных и упускать основной тренд.

Сколько нужно данных?

Известно, что чем больше данных использует модель, тем лучше. Но как нам понять в конкретной ситуации, помогут ли новые данные? Скажем, целесообразно ли нам потратить N\$ на труд асессоров, чтобы увеличить выборку вдвое?

Поскольку новых данных пока может и не быть, разумно поварьировать размер имеющейся обучающей выборки и посмотреть, как качество решения задачи зависит от объема данных, на котором мы обучали модель. Так получаются кривые обучения (learning curves).

Идея простая: мы отображаем ошибку как функцию от количества примеров, используемых для обучения. При этом параметры модели фиксируются заранее.

Давайте посмотрим, что мы получим для линейной модели. Коэффициент регуляризации выставим большим.

Типичная ситуация: для небольшого объема данных ошибки на обучающей выборке и в процессе кросс-валидации довольно сильно отличаются, что указывает на переобучение. Для той же модели, но с большим объемом данных ошибки «сходятся», что указывается на недообучение.

Если добавить еще данные, ошибка на обучающей выборке не будет расти, но с другой стороны, ошибка на тестовых данных не будет уменьшаться.

Получается, ошибки «сошлись», и добавление новых данных не поможет. Собственно, это случай – самый интересный для бизнеса. Возможна ситуация, когда мы увеличиваем выборку в 10 раз. Но если не менять сложность модели, это может и не помочь. То есть стратегия «настроил один раз – дальше использую 10 раз» может и не работать.

Что будет, если изменить коэффициент регуляризации (уменьшить до 0.05)?

Видим хорошую тенденцию – кривые постепенно сходятся, и если дальше двигаться направо (добавлять в модель данные), можно еще повысить качество на валидации.

А если усложнить модель ещё больше ()?

Проявляется переобучение – AUC падает как на обучении, так и на валидации.

Строя подобные кривые, можно понять, в какую сторону двигаться, и как правильно настроить сложность модели на новых данных.

Выводы по кривым валидации и обучения

6. Плюсы и минусы линейных моделей в задачах машинного обучения

7. Домашнее задание № 4

Актуальные домашние задания объявляются во время очередной сессии курса, следить можно в группе ВК и в репозитории курса.

8. Полезные ресурсы

Статья написана в соавторстве с mephistopheies (Павлом Нестеровым). Он же – автор домашнего задания. Авторы домашнего задания в первой сессии курса (февраль-май 2017)– aiho (Ольга Дайховская) и das19 (Юрий Исаков). Благодарю bauchgefuehl (Анастасию Манохину) за редактирование.

Источник