для чего применяется функция mod
Mod и остаток — не одно и то же
Приготовьтесь, вас ждёт крайне педантичная статья, которая вполне может спасти вас на собеседовании или сэкономить несколько часов при вылавливании бага в продакшне!
Я сейчас активно работаю над вторым сезоном «Руководства для самозванца» и пишу о шифре RSA для SSH, который, очевидно, является самым загружаемым фрагментом кода в истории IT.
Хочется полностью разобраться в этой истории. Кто придумал этот шифр, как он работает, почему работает и будет ли работать в будущем. Сейчас я раскопал одну чертовски интересную историю. Я не криптоманьяк и вижу, как других буквально засасывает в эту область. Но мне это тоже интересно, потому что повсюду есть маленькие норки, а меня как сороку привлекают блестящие штучки в глубоких норках. Я также очень хорош в метафорах.
В любом случае: на прошлой неделе я узнал что-то странное и хочу поделиться: оказывается, mod и остаток от деления — не одно и то же. Действительно забавно то, что некоторые читатели при этих словах выпрыгивают со своих кресел и орут: «А ведь именно это я всегда пытался сказать вам и всем остальным!»
Позовите ребят из секты «mod не остаток»! Это для вас.
Что такое mod?
Я должен был изучить это, как и в прошлый раз, когда всплыла такая тема. Это одна из тех вещей, которые ты знаешь, но не запоминаешь. Когда вы применяете mod, то делите одно число на другое и берёте остаток. Итак: 5 mod 2 будет 1, потому что 5/2=2 с остатком 1.
Вот где мы попадаем в странную серую область.
Математика циферблата
Криптографам нравится эта идея, потому что они могут использовать деление с остатком с гигантскими простыми числами для генерации криптографических ключей. Это совсем другая история: если хотите прочитать об этом, то можете купить книгу или, ещё лучше, поддержать мои усилия написать её.
Впрочем, не будем отклоняться от темы.
Остатки и математика циферблата
Теперь переходим к сути: modulo и простой остаток одинаковы, когда числа положительны, но отличаются в случае отрицательных чисел.
Рассмотрим такую задачу:
JavaScript с этим согласен:
Google согласен с первым утверждением, но не согласен со вторым:
Ruby согласен с Google:
Во имя Дейкстры, что здесь происходит?
Вращение часов назад
Чтобы ответить на вопрос, следует понять разницу между остатком и modulo. Программисты объединяют эти операции, но не должны этого делать, потому что они дают одинаковый результат только в случае, если делитель (в нашем случае 12) положителен. Вы можете легко отправить баги в продакшн, если делитель отрицательный.
Но почему существует разница? Рассмотрим положительный делитель 19 mod 12 на часах:
Это известная вещь
Прежде чем назвать меня сумасшедшим и начать гуглить тему: это известный факт. На самом деле MDN (Mozilla Developer Network) даже дошла до того, чтобы назвать % операцией «остатка» (remainder), а не modulo:
Оператор remainder возвращает остаток от деления одного операнда на другой. Он всегда принимает знак делимого.
Вот что Эрик Липперт, один из богов C#, говорит о modulo в C#:
Однако это совсем не то, что оператор % реально делает в C#. Оператор % не является каноническим оператором modulus, это оператор остатка.
А как на вашем языке?
Ну и что?
Могу понять, если вы дочитали досюда, а теперь чешете голову и задаётесь вопросом, стоит ли беспокоиться. Думаю, что стоит по двум причинам:
Оператор Mod
Возвращает остаток от деления двух чисел.
Синтаксис
результат = number1 Mod number2
Синтаксис оператора Mod состоит из следующих частей:
| Part | Описание |
|---|---|
| result | Обязательный элемент; любая числовая переменная. |
| число1 | Обязательный элемент; любое цифровоезначение. |
| число2 | Обязательный элемент; любое цифровое значение. |
Примечания
Оператор модуля (остатка) делит число1 на число2 (числа с плавающей запятой при этом округляются до целого) и возвращает остаток в аргументе результат. Например, в следующем выражении A (результат) равно 5.
Обычно типом данных атрибута результат является Byte, вариант Byte, Integer, вариант Integer, Long или Variant, содержащий значение Long, независимо от того, является ли результат целым числом. Дробные части отсекаются.
Однако если любое из выражений имеет значение Null, объект результат будет иметь значение Null. Любое выражение со значением Empty обрабатывается как 0.
Пример
В этом примере оператор Mod возвращает только остаток от деления двух чисел. Любые числа с плавающей запятой предварительно округляются до целого.
См. также
Поддержка и обратная связь
Есть вопросы или отзывы, касающиеся Office VBA или этой статьи? Руководство по другим способам получения поддержки и отправки отзывов см. в статье Поддержка Office VBA и обратная связь.
Оператор Mod (Visual Basic)
Делит два числа и возвращает только остаток.
Синтаксис
Компоненты
result
Обязательный элемент. Любая числовая переменная или свойство.
number1
Обязательный. Произвольное числовое выражение.
number2
Обязательный. Произвольное числовое выражение.
Поддерживаемые типы
Результат
Remarks
Если number1 или number2 имеет значение Nothing, оно считается нулевым.
К связанным операторам относятся следующие.
оператор \ (Visual Basic) возвращает целочисленное частное от деления. Например, выражение принимает значение 14 \ 4 3.
оператор/(Visual Basic) возвращает полное частное, включая остаток, в виде числа с плавающей запятой. Например, 14 / 4 результатом вычисления выражения является 3,5.
Попыток деления на ноль
Если number2 значение равно нулю, поведение Mod оператора зависит от типа данных операндов:
Эквивалентная формула
Выражение a Mod b эквивалентно любой из следующих формул:
Точность чисел с плавающей запятой
При работе с числами с плавающей запятой Помните, что они не всегда имеют точное десятичное представление в памяти. Это может привести к непредвиденным результатам некоторых операций, таких как сравнение значений и Mod оператор. Дополнительные сведения см. в разделе Устранение неполадок типов данных.
Перегрузка
Mod Оператор можно перегрузить, то есть класс или структура может переопределить его поведение. Если код применяется Mod к экземпляру класса или структуры, включающей такую перегрузку, убедитесь, что вы понимаете его переопределенное поведение. Для получения дополнительной информации см. Operator Procedures.
Пример 1
В следующем примере оператор используется Mod для деления двух чисел и возврата только остатка. Если любое число является числом с плавающей запятой, результатом является число с плавающей запятой, представляющее остаток.
Пример 2
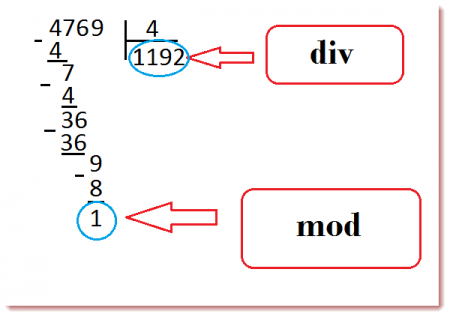
Для чего применяется функция mod
Оператор div и оператор mod
В этой статье речь пойдет о целочисленном делении и делении с остатком.
То есть например 20 / 5 = 4, 55 / 6 = 9, 100 / 3 = 33 и т.д.
Согласитесь, что в некоторых случаях это очень удобно и практично. Теперь поговорим о реализации этого метода в Паскале. Тут все достаточно просто, открывать Америку не придется. В паскале за целочисленное деление отвечает оператор div. Теперь как это записывается в Pascal’e
Таким образом, вот такая запись (55 / 6) нацело = 9 в результате использования оператора div будет выглядеть так
z будет равно 9. Запомните! При использовании оператора div дробная часть будет отброшена!
А сейчас поговорим о делении с остатком. Оно не особо отличается и главным здесь является то, что в результате отбрасывается как раз целая часть. То есть (40 / 6) с остатком = 4, (10 / 3) с остатком =1, (22 /5) с остатком = 2 и т.д. В паскале для этого есть оператор mod. Записывается он точно так же.
Например (40 / 6) с остатком = 4 с оператором mod будет такой
Кстати оператор mod часто используют, для определения кратности чисел (кратность — это делимость на какое-нибудь число нацело. То есть например говорят, что числа 3, 6, 9, 12, 21 кратны трем. Или числа 5,10,15,20 кратны 5). В статье нахождение четных элементов массива я упоминал о числах кратных двум (четных). Итак как эту кратность определить в паскале. Обратите внимание, что если число кратное, то у него есть остаток (точнее оно имеет в остатке ноль). Этим и стоит воспользоваться.
Сейчас я привел пример условия, которое проверяет кратность, где v — это число, проверяемое на кратность по числу m. Например чтобы проверить,
является ли 40 кратным 4, используем оператор mod с условием и получим
«Деление» по модулю
Обычные арифметические операции по модулю выполняются не сильно сложнее — просто нужно брать модули и заботиться о переполнении. Например:
Но вот с делением возникают проблемы — мы не можем просто взять и поделить.
Через бинарное возведение в степень
Этот подход простой и быстрый, однако следует помнить, что он работает только для простых модулей.
Через расширенный алгоритм Евклида
Расширенный алгоритм Евклида можно использовать для решения в целых числах уравнений вида
Преимущества этого метода над возведением в степень:
Но лично автор почти всегда использует возведение в степень.
Упрощенная реализация
Сначала приведем реализацию, а потом поймем, почему она работает:
Докажем по индукции, что функция действительно возвращает обратный элемент.
Во втором случае проверим правильность формулы:
Предподсчет обратных элементов
Чаще всего нам нужно искать обратный элемент в контексте комбинаторики.
Например, особенно часто нужно считать биномиальные коэффициенты, для чего в свою очередь нужно уметь обращать факториалы:
Простой способ — это предпосчитать обычные факториалы и каждый раз вызывать inv один или два раза:
Однако это добавит лишний логарифм в асимптотику в нередком случае, когда какая-то комбинаторная формула лежит внутри горячего цикла. Поэтому имеет смысл предподсчитать и частые обратные элементы.
Обратные факториалы
Все остальные обратные факториалы можно таким же образом итеративно подсчитать из предыдущего.