для чего применяется моделирование методом монте карло
Метод Монте Карло – что это в экономике, примеры
Метод Монте Карло используется для решения различных задач, где результат зависит от случайных процессов. В частности, метод широко используется в экономике, инвестиционных прогнозах и инвестиционном анализе, финансовом планировании. Моделирование по методу Монте Карло позволяет вычислить множество значений. Используя эти значения, определяется искомый результат путем вычисления среднего арифметического или диапазон, в котором может находиться нужный результат.
В этой статье мы расскажем, как применяется метод Монте Карло в экономике, личных финансах и инвестировании. С помощью наглядных примеров попытаемся понять, какие задачи можно решать с применением метода Монте Карло.
Что такое метод Монте Карло (ММК)
Итак, метод Монте Карло позволяет рассчитать какую-либо величину (или диапазон значений) с использованием множества случайных величин.
К примеру, бегун способен пробежать дистанцию в 10 км за 50 мин. Означает ли это, что 20 км он пробежит за 1 час 40 минут? Конечно же, нет: человек – не машина. Если 10 км можно пробежать без остановки, то расстояние вдвое больше требует значительных затрат энергии. Так, необходимо замедлиться, чтобы попить воды, завязать шнурки. При сильном учащении пульса – перейти на шаг или легкий бег и т.д.
Таким образом, прогнозирование времени путем простых математических расчетов – способ, который даст весьма неточный результат. Правильнее будет отобрать в случайном порядке результаты забегов нескольких спортсменов (чем больше, тем лучше) такого же пола, примерно того же возраста и уровня подготовки, которые несколько раз бежали дистанции по 20 км, и вычислить среднее арифметическое результатов. Тогда мы получим значение, на которое можно ориентироваться.
Примерно так работает метод Монте Карло простыми словами. С помощью метода можно вычислять риски. Возвращаясь к нашему примеру, подумаем, какова вероятность того, что спортсмен не пробежит 20 км? Причин может быть масса: внезапная травма, сильная усталость, ситуация на дороге и т.д. Это те самые случайные события, определить вероятность которых невозможно, т.к. они все разные по своей природе. Если все же пользоваться какими-то примерными цифрами или диапазонами значений, то, скорее всего, мы получим такой результат, о котором математики говорят: «задача не имеет решений».
Поэтому следует ориентироваться только на имеющиеся данные, полученные в результате коллективных забегов, когда имели место подобные случаи. Выбрав несколько результатов и сопоставив их с количеством бегунов, пробежавших дистанцию успешно, мы получим средний процент риска.
Для прогнозирования рисков, доходности, сроков окупаемости и других финансовых результатов используется метод Монте-Карло-симуляции. Вероятность события определяется так: программа выбирает комбинации случайных значений (например, неблагоприятных исходов) и на основании этого выдает усредненный результат. Для получения более точного значения симуляцию следует повторить несколько раз. Программное обеспечение применяется различное – от знакомого нам всем Excel до узкоспециализированных программных продуктов, используемых финансовыми аналитиками, физиками, программистами, трейдерами и др.
История
Откуда метод получил свое название? В Европе есть маленькое княжество Монако, где одна из территорий названа Монте-Карло. Это такой европейский Лос-Анджелес, где можно окунуться в роскошь и азартные развлечения. От знаменитого казино метод Монте-Карло получил свое имя.
Впервые о методе заговорили в конце 40-х годов прошлого столетия, когда ВВС США начало разработку водородной бомбы. Тогда, с появлением первых ЭВМ, было предложено использовать теорию вероятностей для решения прикладных задач.
Далее, в 1970-х годах, метод получил применение в нейтронной физике для задач, не поддающихся решению традиционными математическими методами. Впоследствии моделирование по методу Монте-Карло распространилось на другие области физики, а также на экономику и вычислительную математику.
Схема метода
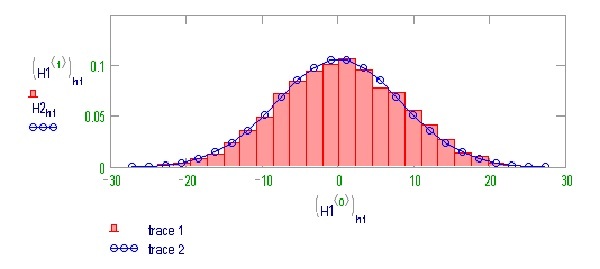
Имитационное моделирование по методу Монте-Карло представляет собой определение математического ожидания (среднего значения случайной величины) путем проведения определенного количества симуляций (испытаний).
Предположим, требуется найти математическое ожидание α для случайной величины \( X \) :
Классическая формула расчета математического ожидания выглядит так:
\( x1…n \) – значение величины от 1 до n;
\( p1…n \) – вероятность от 1 до n.
Моделирование методом Монте-Карло выполняется следующим образом: проводится n симуляций (испытаний). В результате получится какое-то количество значений X. Далее определяется их среднее арифметическое, которое и будет приблизительным значением α.
Зачем нужен ММК и где он применяется
Чтобы не углубляться в математические дебри, сформулируем кратко суть метода.
Метод Монте-Карло относится к методам моделирования различных явлений, событий, параметров или процессов, как благоприятных, так и неблагоприятных, с целью определения вероятности их наступления. Для этого генерируется определенное количество случайных величин, отвечающих установленным критериям, а затем на их основе вычисляют приблизительное значение искомой величины.
ММК применяется в следующих областях:
По сути, методу можно найти применение во многих сферах, где необходимы расчеты и прогнозирование.
Входные данные
Данные для получения искомой величины определяются путем стохастической (случайной) выборки. Чтобы было более понятно, приведем простейший пример из компьютерных игр.
Предположим, у нас есть компьютерная игра, в которую мы играли много-много раз. При этом ведется статистика: сыграно 100 игр, из них 30 побед, 70 поражений. Это и будет нашими входными данными. А решение будет таким: вероятность победы – 30%, проигрыша – 70%.
Можно использовать метод Монте-Карло для симуляции инвестиционного портфеля. Предположим, нам нужно получить доходность не менее 10%. Для этого подбираем инструменты с доходностью не меньше этой величины и вычисляем среднее арифметическое. Составляющие портфеля можно варьировать для получения максимальной доходности. Здесь входными данными будут наименование, стоимость и доходность отдельного инструмента, а искомым значением – общая доходность портфеля.
Процесс моделирования методом Монте-Карло
Имитационное моделирование методом Монте-Карло – это автоматизированный процесс, позволяющий рассматривать вероятность наступления различных событий. Каждая смоделированная ситуация является уникальной, что дает возможность оценить целый спектр рисков.
При создании модели все неопределенные факторы заменяются диапазоном возможных значений. К примеру, ни один аналитик, занимающийся оценкой рисков, не может знать, каким будет курс евро через 3-5 лет. Программа позволяет задать диапазон значений на усмотрение специалиста. Разумеется, здесь многое зависит от человека: требуется определенный уровень квалификации.
Далее система распределяет вероятности. Для оценки различных параметров применяются варианты распределения:
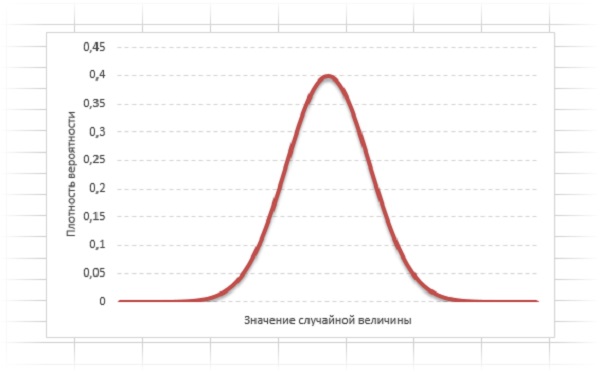
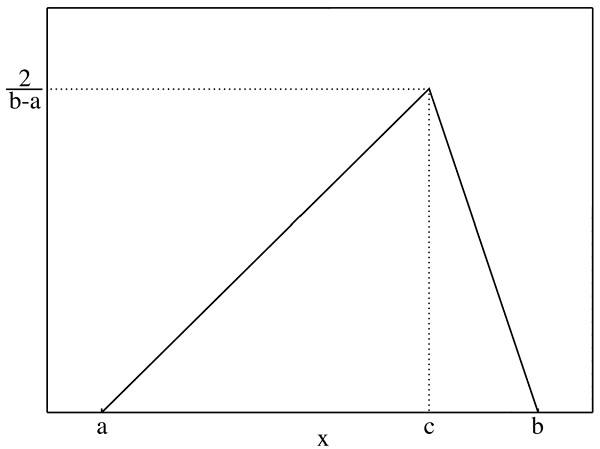
Значение случайной величины, расположенное посередине, характеризует наиболее высокую вероятность. Для построения кривой используются статистические данные: ожидаемое значение и стандартное отклонение. Такой вариант распределения подойдет, к примеру, для расчета стоимости коммунальных услуг в обозримом будущем.
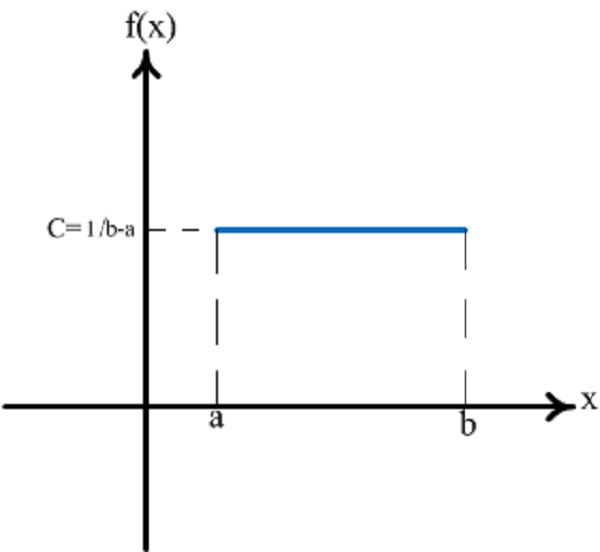
Кривая равномерного распределения имеет вид прямоугольника. На графике a и b – минимальные значения, С – вероятность. Подойдет для расчета условно-постоянных расходов в краткосрочном периоде.
Итак, имитационное моделирование по методу Монте-Карло выполняется многократно. По результатам всех операций делается выборка значений, результаты систематизируются и определяется итоговая вероятность события.
Выходные данные
Выходными или итоговыми данными имитационного моделирования по методу Монте-Карло могут быть числовые значения или проценты. В отдельных случаях значения могут находиться внутри диапазона.
Однако итоги тестирования выражаются не только в цифрах. Возможно также выявление каких-то функций или параметров в модели, которые оказывают наибольшее влияние на результат. К примеру, наибольшее влияние на курс рубля оказывают цены на нефть на мировом рынке.
Сколько имитационных испытаний необходимо выполнить
Количество симуляций зависит от цели исследования. Как уже упоминалось, моделирование повторяется сотни, тысячи, иногда десятки тысяч раз – чем больше испытаний, тем более достоверный результат будет получен на выходе. При наличии программы не возникает проблем в многократном повторении операции.
Преимущества и недостатки метода
Достоинствами ММК являются:
Примеры
Перейдем к практическим примерам использования метода Монте-Карло.
Пример 1. Рассмотрим ситуацию, когда 35-летний человек планирует уйти на пенсию в 60 лет.
Таким образом, цель – накопить 300000$ (1000х12/0.04). Проверим вероятность этой суммы, используя симулятор. Программа выполнит 125000 симуляций (5000х25 лет).
Итак, по первой строчке мы видим, что в 99,7% симуляций цель будет выполнена.
Пример 2. При тех же условиях зададим размер капитала, который мы планируем сохранить на конец периода. Для удобства примем эту сумму равной размеру начального капитала.
Здесь процент вероятности благоприятного развития событий уменьшился до 84,3%. Что с этим можно сделать?
Когда я смогу накопить
Метод Монте-Карло является примером подхода к моделированию на основе результатов анализа взаимосвязей между явлениями. В наших примерах эту взаимосвязь можно охарактеризовать так: доходность инвестиций → инфляция → волатильность портфеля → капитал.
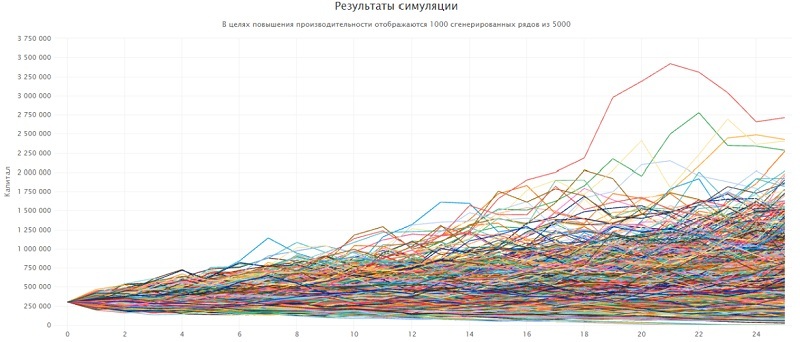
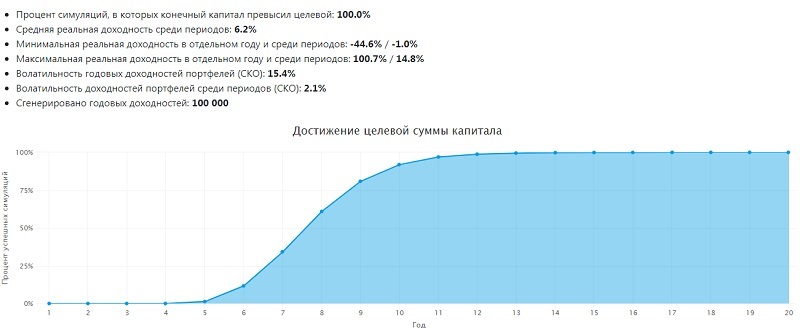
Не стоит забывать и о том, что в любую модель могут вноситься коррективы под влиянием воли человека. Причиной тому могут быть непредвиденные обстоятельства, которые случаются в жизни каждого, а уж за анализируемый нам 25-летний период их будет немало. Тем не менее, рассмотрим «обратный» пример, где цель – не сохранить, а наоборот, накопить тот самый капитал в 300000$, необходимый для того, чтобы обеспечить безбедную старость.
Из графика видно, что нужная сумма накопится примерно на 13-м году. Не следует забывать о падениях рынка, которые случаются раз в несколько лет. Вместе с тем, некоторые активы могут взлететь в цене, что принесет крупный незапланированный доход. Но ориентироваться лучше на срок с запасом в 2-3 года, т.е. примерно 15-16 лет с точки отсчета.
Заключение
Мы разобрали метод Монте-Карло от самых простых основ, «для чайников», до описания зависимостей между процессами и примеров имитаций с помощью программных средств. Углубляться в математические функции и вспоминать теорию вероятности не стоит, тем более что мало кто в наше время будет заниматься моделированием вручную.
Достаточно понять, что метод Монте-Карло основан на моделировании случайных процессов на основании заданных пользователем исходных данных. ММК успешно применяется там, где обычные математические расчеты могут дать недостоверные результаты.
Предусмотреть все случайности с вероятностью 100% сложно, поэтому метод допускает определенную погрешность, которая частично компенсируется количеством произведенных симуляций.
Моделирование методом Монте-Карло имеет множество применений в финансовой практике, связанных с анализом сложных случайных процессов, в том числе в финансовом планировании, стоимостной оценке рисков (VaR), оценке стоимости сложных опционов и других финансовых активов. Рассмотрим концепцию моделирования методом Монте-Карло в рамках изучения количественных методов по программе CFA.
Разобравшись в основах распределений вероятности, мы теперь готовы узнать о компьютерном методе, в котором вероятностные распределения играют важную роль. Этот метод называется моделированием методом Монте-Карло, статистическим моделированием или имитационным моделированием (англ. ‘Monte Carlo simulation’).
Моделирование методом Монте-Карло в области финансов предполагает использование компьютера для имитации функционирования сложной финансовой системы.
Характерной особенностью моделирования методом Монте-Карло является генерация большого числа случайных выборок из заданного распределения вероятностей или распределений, характеризующих риск в рассматриваемой системе.
Исследователь Стэнфордского университета Сэм Сэведж представил следующую довольно точную аналогию роли этого метода:
Так же, как встряхивание лестницы помогает нам оценить риски падения с лестницы, моделирование методом Монте-Карло позволяет экспериментировать с предлагаемой финансовой стратегией или политикой до ее фактического осуществления. Например, показатели инвестиционной деятельности можно оценить относительно эталона или обязательства.
Пенсионные планы с установленными выплатами часто предполагают вложение свободных активов в зависимости от запланированного погашения пенсионных обязательств.
Пенсионные обязательства представляют собой сложный случайный процесс. В финансовом планировании активов и обязательств с использованием метода Монте-Карло, функционирование пенсионных активов и обязательств моделируется на определенный временной период, с учетом допущений о том, как инвестируются активы и других случайных величин.
Ключевым моментом в этой имитации и методе Монте-Карло является распределение вероятностей для различных источников риска (в том числе процентных ставок и ставок доходности рынка ценных бумаг, в данном случае).
Последствия решений инвестиционной политики пенсионного фонда можно оценить с помощью моделирования на определенный период. Эксперимент можно повторить для другого набора допущений.
В приведенном ниже Примере (11) серия ставок доходности не достаточно велика, чтобы ответить на вопросы аналитиков о временных закономерностях фондового рынка, поэтому исследователи моделируют рыночную доходность, чтобы найти ответы на свои вопросы.
Моделирование методом Монте-Карло также широко используется для получения стоимостной оценки риска VaR. В этом случае мы моделируем показатель прибыли и убытков портфеля в течение определенного промежутка времени.
Повторные испытания в рамках моделирования (каждое испытание означает получение случайных наблюдений из распределения вероятностей) создают частотное распределение для оценки стоимости портфеля. Например, точка, которая определяет порог отсечения, по меньшей мере, 5% благоприятных моделируемых изменений, является 95%-ной оценкой риска VaR.
Чрезвычайно важным применением моделирования методом Монте-Карло является оценка сложных ценных бумаг, в частности, некоторых европейских опционов, для которых не существует аналитической формулы ценообразования.
Для других ценных бумаг, таких как ипотечные ценные бумаги со сложными встроенными опционами, моделирование методом Монте-Карло также является важным аналитическим инструментом.
Исследователи используют моделирование методом Монте-Карло, чтобы проверить свои модели и инструменты.
Насколько критично конкретное предположение об эффективности модели?
Поскольку мы управляем предположениями, когда делаем имитацию, мы можем выполнить моделирование методом Монте-Карло, чтобы исследовать чувствительность модели к изменению наших предположений.
Процесс моделирования методом Монте-Карло.
Чтобы понять технику моделирования методом Монте-Карло, давайте представим процесс в виде серии шагов.
Для того, чтобы проиллюстрировать эти шаги, мы рассмотрим пример использования метода Монте-Карло для оценки азиатского колл-опциона, не имеющего аналитической формулы ценообразования.
Шаг 1. Определите интересующие величины (стоимость опциона, например, или размер активов пенсионного плана) в терминах базовых случайных величин.
Базовой случайной величиной (или несколькими величинами) может быть цена акций опциона, рыночная стоимость пенсионных активов, или другие случайные величины, связанные с обязательствами по пенсионному плану.
Укажите первоначальные значения базовых случайных величин.
Для иллюстрации шагов, мы используем оценку азиатского колл-опциона: \( С_
Каждое имитационное испытание требует генерации случайной величины (итерация Шага 4).
Шаг 2. Определите временную шкалу. Возьмите календарный временной горизонт и разделить его на несколько подпериодов, общим числом \(K\).
Календарный период разделенный на \(K\) подпериодов, имеет временной инкремент (приращение времени) \(\Delta t\).
Шаг 3. Сделайте предположения о характере распределения для факторов риска, которые влияют на базовые случайные величины.
Например, цена акций является базовой случайной величиной для азиатского колл-опциона, поэтому нам нужна модель движения цен на акции. Допустим, мы выбираем следующую модель движения цен на акции, где \( Z_k \) обозначает стандартную нормальную случайную величину:
\(\Delta t\)(Цена акций) = (\( \mu \times \) Предыдущая цена акций \(\times \Delta t\)) + (\( \sigma \times \) Предыдущая цена акций \(\times Z_k \))
В данном случае, \( Z_k \) является фактором риска при моделировании. Выбирая значение \( \mu\) и \( \sigma\), мы контролируем распределение стоимости акций. Хотя в этом примере используется один фактор риска, данная имитация может иметь несколько факторов риска.
Шаг 4. С помощью компьютерной программы или функции Excel, сгенерируйте \(K\) случайные наблюдения для каждого фактора риска.
Шаг 5. Вычислите базовые случайные величины, используя случайные наблюдения, сгенерированные на Шаге 4.
Результатом описанной выше модели динамики цены акций будет \(K\) наблюдений изменений цены акций. Для преобразования этих изменений в \(K\) цен на акции необходим дополнительный расчет (с использованием первоначальных цен акций, определенных на Шаге 1).
Другой расчет вычисляет среднюю цену акций в течение срока действия опциона (т.е. сумма \(K\) цен на акции делятся на \(K\)).
Шаг 6. Рассчитайте интересующие величины.
В нашем примере, первый расчет определяет стоимость азиатского колл-опциона на момент исполнения, \( С_
Мы выполнили одно имитационное испытание (Нижний индекс \(i\) в \( С_
При моделировании методом Монте-Карло, в табличной форме записываются статистические данные каждого испытания, касающиеся распределения интересующих нас величин, в том числе их средние значения и стандартные отклонения.
Шаг 7. Итеративно возвращайтесь к Шагу 4, пока не выполните все \( I \) испытаний.
И, наконец, рассчитайте итоговые статистические данные для всех имитаций. Ключевым значением в нашем примере является среднее значение \( С_
Сколько имитационных испытаний необходимо выполнить?
Как правило, нам нужно увеличить количество испытаний на коэффициент 100, чтобы увеличить точность испытания на 1 знак.
В зависимости от задачи, могут потребоваться десятки тысяч испытаний, чтобы получить точность до 2 знаков после запятой (например, это требуется стоимости опциона).
Проведение большого количества испытаний не обязательно проблематично, учитывая нынешние вычислительные мощности (даже обычного пользовательского ПК). Необходимое число имитационных испытаний может быть уменьшено с использованием специальных процедур понижения дисперсии, но эта тема выходит за рамки данного чтения.
Генераторы случайных чисел и процедура генерации случайных наблюдений.
На Шаге 4 нашего примера, компьютер генерирует набор случайных наблюдений для стандартной нормальной случайной величины. Напомним, что для равномерного распределения все возможные исходы равновероятны.
Термин «генератор случайных чисел» (англ. ‘random number generator’) относится к алгоритму, который возвращает равномерно распределенные случайные числа между 0 и 1.
В контексте компьютерного моделирования, термин «случайное число» (англ. ‘random number’) относится к наблюдению из равномерного распределения.
Для других распределений в данном контексте используется термин «случайное наблюдение» (англ. ‘random observation’).
Числа, возвращаемые генераторами случайных чисел, зависят от «зерна» или начального значения (от англ. ‘seed’). Если то же самое зерно передается в качестве параметра в тот же генератор, он будет возвращать ту же самую последовательность случайных чисел.
Замечательным фактом является то, что случайные наблюдения из любого распределения можно получить с использованием равномерной случайной величины в диапазоне от 0 до 1.
Для того, чтобы лучше понять это, рассмотрим метод обратной трансформации случайных наблюдений (англ. ‘inverse transformation method’).
Предположим, что мы заинтересованы в получении случайных наблюдений для случайной величины \(X \), с кумулятивной функцией распределения \( F(x) \). Напомним, что \( F(x) \), рассчитанная в точке \(x\), представляет собой число между 0 и 1.
Предположим, что случайный исход этой случайной величины равен 3.21 и что \(F(3.21) = 0.25\) или 25%.
Определим обратную функцию \(F\) и назовем ее \( F^ <-1>\). Она может сделать следующее: подставим вероятность 0.25 в функцию \( F^ <-1>\), и она вернет случайный результат 3.21. Другими словами, \( F^<-1>(0.25)=3.21 \).
Для генерации случайных наблюдений величины \( X \), выполняются следующие шаги:
Генерация случайного наблюдения сама по себе является областью отдельного изучения, и здесь мы лишь кратко обсудили метод обратной трансформации.
Далее, в Примерах 11 и 12, мы проиллюстрируем, как моделирование методом Монте-Карло позволяет определить потенциальную выгоду от выбора момента сделки (рыночного тайминга).
Пример (11) определения потенциальной прибыли от рыночного тайминга: метод Монте-Карло (1).
Насколько точно инвестор должен прогнозировать бычий рынок (англ. ‘bull market’) и медвежий рынок (англ. ‘bear market’), чтобы получать прибыль?
Какой размер прибыли по сравнению со стратегией «покупать и держать» можно получить при заданной точности прогнозирования рынка?
Из-за большой изменчивости доходности активов, необходим огромный объем данных о доходности, чтобы получить статистически достоверные ответы на эти вопросы.
Поэтому исследователи Chua, Woodward и To (1987) выбрали метод Монте-Карло для определения потенциальной прибыли от рыночного тайминга. Их интересовали перспективы канадских инвесторов.
Чтобы понять их исследование, предположим, что в начале года инвестор прогнозирует, что в следующем году будет либо бычий рынок, либо медвежий рынок.
Инвестиционные результаты тех, кто использует рыночный тайминг можно сравнить с результатами тех, кто придерживается долгосрочной стратегии buy-and-hold. Долгосрочный инвестор получает рыночный доход ежегодно.
Для Chua и др. одним из интересующих показателей был выигрыш от рыночного тайминга. Они определили эту величину как среднюю доходность маркет-таймера за вычетом средней доходности долгосрочного инвестора.
С учетом этих параметров, моделируемая рыночная доходность будет:
\( R_
Используя второй набор 10 000 случайных стандартных нормальных наблюдений, историческую доходность канадских казначейских векселей, а также историческую корреляцию векселей и доходности акций, авторы сгенерировали 10 000 ставок доходности казначейских векселей.
Инвесторы могут обладать различными навыками и опытом прогнозировании бычьих и медвежьих рынков. Chua и др. охарактеризовали маркет-таймеров по точности прогнозирования бычьих рынков и точности прогнозирования медвежьих рынков.
Например, точность прогнозирования бычьего рынка в 50% означает, что, если маркет-таймер прогнозирует бычий рынок на следующий год, он оказывается прав только в половине случаев, что указывает на отсутствие навыка.
Мы можем смоделировать, насколько инвестор будет точен.
После генерации первого наблюдения для \( R_
Если наблюдение соответствует бычьему рынку, то 0.60 (точность прогноза на бычьем рынке) сравнивается со случайным числом (от 0 до 1).
Если случайное число оказывается меньше, чем 0.60, что происходит с вероятностью 60%, то предполагается, что маркет-таймер правильно предсказал бычий рынок и его доходность для этого первого наблюдения является рыночной ставкой доходности.
Если случайное число оказывается больше, чем 0.60, то предполагается, что маркет-таймер допустил ошибку и предсказал медвежий рынок. Его доходность для этого наблюдения является безрисковой ставкой доходности.
Аналогичным образом, если это первое наблюдение соответствует медвежьему рынку, маркет-таймер имеет 80-процентный шанс быть правым в прогнозировании медвежьего рынка на основе генерации случайных чисел.
В любом случае, доходность инвестора сравнивается с рыночной доходностью, чтобы зафиксировать его выигрыш (разницу) по сравнению с долгосрочной стратегией buy-and-hold.
Описанный выше процесс является одним имитационным испытанием (итерацией).
Сымитированной средней доходностью, заработанной маркет-таймером, будет средняя заработанная доходность по итогу всех испытаний в моделировании.
Для того, чтобы лучше понять этот процесс, рассмотрим гипотетическое моделирование методом Монте-Карло с четырьмя испытаниями для маркет-таймера 60-80 таймера (напомним, что это означает 60% точность в прогнозировании бычьих рынков и 80% точность в прогнозировании медвежьих рынков).
В Таблице 8 приведены данные для моделирования.
Давайте взглянем на испытания 1 и 2.
В испытании 1, первое сгенерированное случайное число приводит к рыночной доходности 0.121. Поскольку рыночная доходность 0.121, превысила безрисковую доходность по векселю 0.050, мы имеем дело с бычьим рынком.
Затем мы генерируем случайное число 0.531, которое мы потом сравниваем с точностью маркет-таймера для бычьего рынка, 0.60. Поскольку 0.531 меньше, чем 0.60, то предполагается, что маркет-таймер правильно спрогнозировал бычий рынок и, соответственно, вложился в акции. Таким образом, в этом испытании маркет-таймер получает рыночную доходность 0.121.
В испытании 2 мы наблюдаем еще один бычий рынок, и, поскольку случайное число 0.725 больше, чем 0.60, то предполагается, что маркет-таймер сделал ошибку и предсказал медвежий рынок. Таким образом, таймер заработал безрисковую доходность 0.081, а не более высокую рыночную доходность.