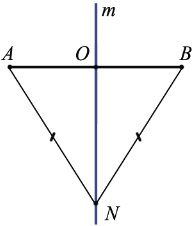
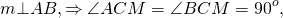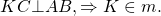докажите что серединный перпендикуляр к отрезку является его осью симметрии
Свойства серединного перпендикуляра
Рассмотрим свойства серединного перпендикуляра. Начнем со свойства серединного перпендикуляра к отрезку.
I) Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
II) И обратно: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
I)
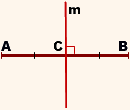
AB- отрезок, C — середина AB,
m — серединный перпендикуляр к AB,
1. Если точка M совпадает с точкой C.
Так как AC=BC по условию, то и AM=BM.
2. Если точка M не совпадает с точкой C.
Рассмотрим треугольники ACM и BCM
то есть треугольники ACM и BCM — прямоугольные.
AC=BC (по условию), CM — общий катет.
Из равенства треугольников следует равенство соответствующих сторон: AM=BM.
Что и требовалось доказать.
II) Дано: AB — отрезок, C — середина AB,
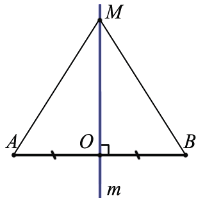
m — серединный перпендикуляр к AB,
Так как AK=BK (по условию), то треугольник AKB — равнобедренный с основанием AB (по определению). Так как C — середина AB, то KC — медиана треугольника AKB.
По свойству равнобедренного треугольника медиана, проведенная к основанию, является также его высотой, то есть
Что и требовалось доказать.
Геометрическое место точек, равноудаленных от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки.
В следующий раз рассмотрим свойство серединных перпендикуляров к сторонам треугольника.
Свойства серединного перпендикуляра к отрезку
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.
— серединный перпендикуляр к отрезку АВ.
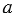
Теорема
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
Обратно: каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.
Доказательство
Доказать: АМ = ВМ
Доказательство:
Доказать: N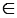
m
Доказательство:
Рассмотрим произвольную точку N.
Если N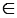АВ, то N = О, а, значит, она лежит на прямой m.
Следствие 1
| Геометрическим местом точек плоскости, равноудалённых от концов отрезка, является серединный перпендикуляр к этому отрезку. |
Следствие2
| Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. |
Поделись с друзьями в социальных сетях:
Серединный перпендикуляр к отрезку:
Рассмотрим понятие серединного перпендикуляра к отрезку.
Определение. Серединным перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.
Следующая теорема характеризует свойства точек серединного перпендикуляра к отрезку.
Теорема 5 (о серединном перпендикуляре). Каждая точка серединного перпендикуляра к отрезку находится на равном расстоянии от концов этого отрезка. Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
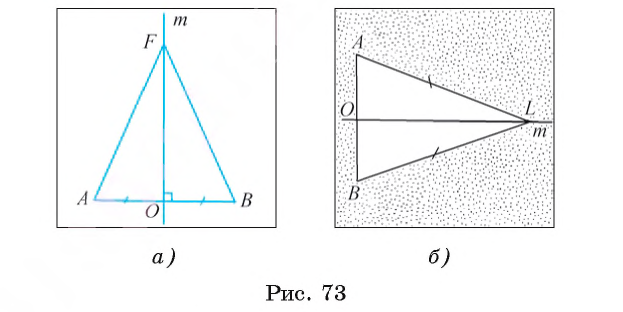
1) Пусть прямая m — серединный перпендикуляр к отрезку АВ, точка О — середина отрезка АВ (рис. 73, а).
Пусть точка F — произвольная точка серединного перпендикуляра. Докажем, что FА = FВ. Если точка F совпадает с точкой О, то это равенство верно, так как точка О — середина отрезка АВ. Пусть точка F не совпадает с точкой О. В этом случае треугольник АОF равен треугольнику ВОF по первому признаку равенства треугольников (АО = ОВ по условию, сторона ОF — общая, 
90°). Отсюда следует, что АF = ВF.
2) Пусть точка L равноудалена от концов отрезка АВ, т. е. АL = ВL (рис. 73, б). Докажем, что точка L лежит на прямой m. Если точка L лежит на прямой АВ, то она совпадает с серединой О отрезка АВ, т. е. лежит на прямой m. Если точка В не лежит на прямой АВ, то треугольник АLВ равнобедренный. Отрезок LO — медиана этого треугольника, а следовательно, и высота. Таким образом, LО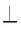
АВ, а, значит, прямые LО и m совпадают. Отсюда вытекает, что точка L лежит на прямой m.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Серединный перпендикуляр к отрезку
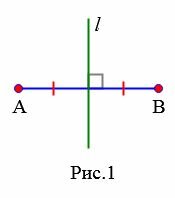
Определение 1. Серединным перпендикуляром к отрезку называется прямая, которая проходит через середину отрезка и перпендикулярная к нему.
 |
Теорема о серединном перпендикуляре к отрезку
Теорема 1. 1) Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. 2) Обратно: Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
 |
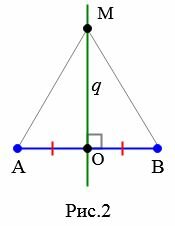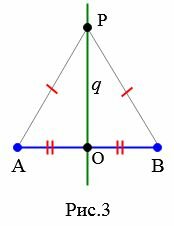
Доказательство. 1) Пусть точка \( \small O \) середина отрезка \( \small AB \) и пусть прямая \( \small q \) серединный перпендикуляр к отрезку \( \small AB \) (Рис.2). Рассмотрим любую точку \( \small M \) на прямой \( \small q \). Докажем, что \( \small AM=BM. \) Если точка \( \small M \) совпадает с точкой \( \small O \), то равенство \( \small AM=BM \) верно поскольку \( \small AO=BO \) (\( \small O \)-середина отрезка). Пусть \( \small M \) и \( \small O \) различные точки. Тогда прямоугольные треугольники \( \small MOA \) и \( \small MOB \) равны по двум катетам (\( \small AO=OB \), \( \small OM \)− общий). Следовательно \( \small AM=BM. \)
 |
Серединный перпендикуляр
Что такое серединный перпендикуляр к отрезку? Что можно сказать о пересечении серединных перпендикуляров к сторонам треугольника? К сторонам многоугольника?
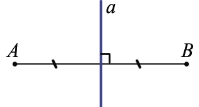
Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через его середину.
m — серединный перпендикуляр к отрезку AB, если
точка C — середина отрезка AB,
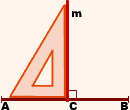
Чтобы построить серединный перпендикуляр к данному отрезку с помощью угольника, нужно:
1) найти середину отрезка;
2) провести через эту точку прямую, перпендикулярную данному отрезку (для этого угольник прикладываем прямым углом к середине отрезка так, чтобы она сторона угольника проходила через отрезок, а через другую сторону проводим прямую):
Свойства серединного перпендикуляра.
1) Геометрическое место точек, равноудаленных от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки.
Например, прямая m — геометрическое место точек, равноудаленных от точек A и B (рисунок 1).
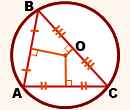
2) Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Эта точка является центром описанной около треугольника окружности.
3) Если около многоугольника можно описать окружность, то центр этой описанной окружности является точкой пересечения серединных перпендикуляров к сторонам многоугольника.