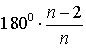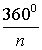докажите что внешний угол треугольника
Внешний угол треугольника
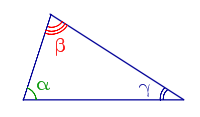
Внешний угол треугольника — это угол, смежный с любым из внутренних углов треугольника.
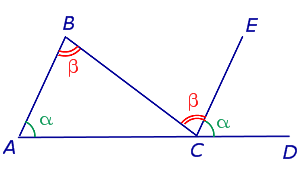
При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:
Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°:
Сумма внутренних углов углов любого треугольника тоже равна 180°, значит:
Из этого следует, что
Сократив обе части полученного равенства на одно и тоже число (∠4), получим:
Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.
Сумма внешних углов
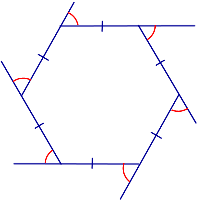
Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360°
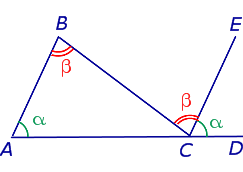
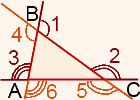
Рассмотрим треугольник ABC:
Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180°. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540°:
(∠1 + ∠4) + (∠2 + ∠5) + (∠3 + ∠6) = 180° + 180° + 180° = 540°.
Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:
Внешний угол треугольника
Углы треугольника бывают внутренние и внешние. Что такое внешний угол треугольника? Как его найти?
Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине.
Как построить внешний угол треугольника? Нужно продлить сторону треугольника.
∠3 — внешний угол при вершине А,
∠2 — внешний угол при вершине С,
∠1 — внешний угол при вершине В.
Сколько внешних углов у треугольника?
При каждой вершине треугольника есть два внешних угла. Чтобы построить внешний угол при вершине треугольника, можно продлить любую из двух сторон, на которых лежит данная вершина. Таким образом получаем 6 внешних углов.
Поэтому, когда говорят о внешнем угле треугольника, не важно, какую из сторон треугольника продлили.
Чему равен внешний угол?
Теорема (о внешнем угле треугольника)
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
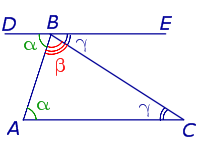
Дано : ∆АВС, ∠1 — внешний угол при вершине С.
∠1 и ∠С (∠АСВ) — смежные, поэтому их сумма равна 180º, значит, ∠1=180º-∠С=180º-(180º-(∠А+∠В))=180º-180º+(∠А+∠В)=∠А+∠В.
Теорема о внешнем угле треугольника.
Теорема. Внешний угол произвольного треугольника больше любого внутреннего угла треугольника, не смежного с ним.
Если существует угол ∠ BCD — внешний угол треугольника ABC, то для него требуется обосновать, что ∠BCD >∠ B и ∠ BCD > ∠A.
Для обоснования осуществим построение, последствием которого внешний угол BCD разделится на две части.
1. Прочертим медиану АО треугольника ABC.
3. Прочертим отрезок ЕС.
Далее проанализируем полученные треугольники АОВ и СОЕ. В указанных треугольниках
Углы АОВ и СОЕ одинаковы, как вертикальные.
Из этого получаем, что треугольник АОВ идентичен треугольнику СОЕ (по двум одинаковым сторонам и углу между ними, т. е. по 1-му признаку равенства треугольников).
Из равенства треугольников можем заключить, что ∠ B = ∠ BCE, поскольку они расположены в одинаковых треугольниках напротив одинаковых сторон АО и ОЕ. И все таки, угол ВСЕ лишь составная часть внешнего угла BCD, и значит, весь внешний угол BCD больше внутреннего угла В. Аналогичным образом обосновываем, что внешний угол BCD больше внутреннего угла А (при данном варианте доказательства построение начинаем с того что прочертим в треугольнике ABC медиану к стороне АС).
На сновании выше доказанной теоремы получаем три следствия, существенно упрощающие обоснование отдельных теорем.
1. В тупоугольном треугольнике лишь один угол тупой, прочие острые, поскольку внешний угол, смежный с тупым внутренним углом,- острый, следовательно, всякий из оставшихся внутренних углов также острый.
2. В прямоугольном треугольнике лишь один угол прямой, прочие острые, поскольку внешний угол, смежный с прямым внутренним углом также прямой, следовательно, всякий из оставшихся внутренних углов будет острым.
3. Из всякой точки, взятой вне прямой, есть возможность прочертить к этой прямой исключительно один единственный перпендикуляр, поскольку, допустив, что из указанной точки существует и второй перпендикуляр к выбранной прямой, мы имели бы треугольник, внешний угол которого был равен внутреннему углу, не смежному с ним, что не соответствует доказанной теореме.
Внешний угол треугольника – определение и свойство
Внешний угол треугольника редко используется при решении геометрических задач. Однако при этом свойства внешнего угла лучше знать, потому как задача на применение этих свойств рано или поздно попадется каждому ученику.
Внешний угол
Внешний угол треугольника это угол, смежный с внутренним. Внутренних углов в треугольнике три, и их сумма равняется 180 градусам. Смежными углами зовутся углы, одна из сторон которых лежит на одной прямой, а вторая является общей.
Что нужно сделать, чтобы увидеть внешний угол треугольника? Для этого придется выполнить некоторые дополнительные построения. Чтобы увидеть внешний угол треугольника необходимо продолжить его сторону. При каждой вершине две стороны, соответственно продолжить можно две прямых и смежных углов будет два.
Рис. 1. Внешние углы треугольника.
Итого в треугольнике получается 6 внешних углов.
Нежелательно на рисунке строить два внешних угла при одной вершине одновременно. Это усложнит построение и, чаще всего, не принесет никакого положительного результата.
Свойства внешних углов
Свойств у внешних углов треугольника не так много и все они связаны с определением внешнего угла.
Основное свойство гласит, что внешний угол треугольника равен сумме двух внутренних углов не смежных с ним. Свойство доказывается достаточно просто. Сумма смежных углов равна 180. Сумма углов в треугольнике все те же 180. Тогда, если обозначить внутренние углы а,в,с, внешний угол d, то:
Вычтем из первого выражения второе и получим:
d=в+с – вот и все доказательство.
Рис. 2. Рисунок к доказательству.
Есть еще несколько дополнительных свойств внешних углов:
Особенное значение имеют внешние углы при решении тупоугольных треугольников. Дело в том, что в тупоугольном треугольнике одна из высот всегда внешняя. Найти эту высоту можно через тригонометрические функции. Для этого и нужно знать угол, который для тупоугольного треугольника будет внешним, а для достроенного прямоугольного треугольника – внутренним.
Рис. 3. Внешний угол тупоугольного треугольника.
Что мы узнали?
Мы привели определение внешнего угла треугольника. Посчитали количество внешних углов треугольника, определили особенности построения внешних углов при решении задачи. Рассказали, где чаще всего применяются свойства внешних углов треугольника.
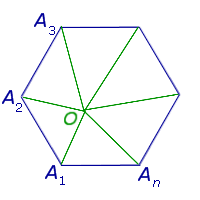
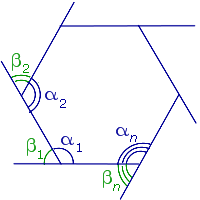
Многоугольники
 Определение многоугольника Определение многоугольника |
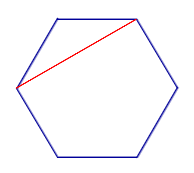
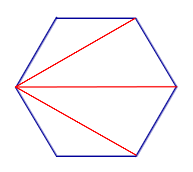
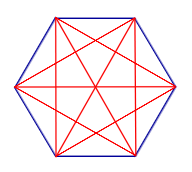
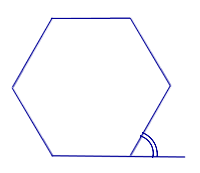
 Диагонали n – угольника Диагонали n – угольника |
 Внешний угол многоугольника Внешний угол многоугольника |
 Свойства углов треугольника Свойства углов треугольника |
 Свойства углов многоугольника Свойства углов многоугольника |
 Свойства углов правильного n – угольника Свойства углов правильного n – угольника |
 Доказательства теорем о свойствах углов многоугольника Доказательства теорем о свойствах углов многоугольника |
Определение многоугольника
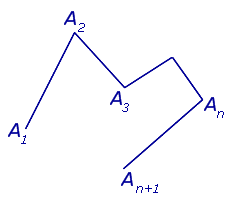
Рассмотрим n отрезков
причём таких, что два любых отрезка, имеющих общий конец, не лежат на одной прямой (рис.1).
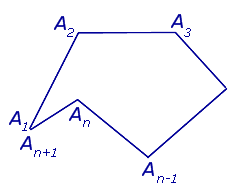
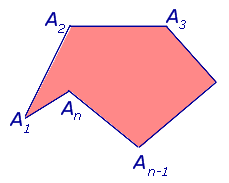
В случае, когда точки A1 и An +1 совпадают, ломаную линию называют замкнутой ломаной линией (рис. 2), в противном случае её называют незамкнутой (рис.1).