В озере живут караси и окуни подсчитано что

В озере живут караси и окуни подсчитано что

Решение задач по теме «Количество информации» (10кл)

Пример 1. В коробке 32 карандаша, все карандаши разного цвета. Наугад вытащили красный. Какое количество информации при этом было получено?

Пример 2.В коробке 50 шаров, из них 40 белых и 10 чёрных. Определить количество информации в сообщении о вытаскивании наугад белого шара и чёрного шара.

Решение.
Вероятность вытаскивания белого шара
P₁ = 40/50 = 0,8
Вероятность вытаскивания чёрного шара
P₂ = 10/50 = 0,2
Количество информации о вытаскивании белого шара I₁ = log₂(1/0,8) = log₂1,25 = log1,25/log2 = 0,32 бит
Количество информации о вытаскивании чёрного шара I₂ = log₂(1/0,2) = log₂5 = log5/log2 » 2,32 бит
Ответ: 0,32 бит, 2,32 бит

Пример 4. Какое количество информации несет в себе сообщение о том, что нужная вам программа находится на одной из восьми дискет?

Пример 5. Заполнить пропуски числами:

а) 5 Кбайт = __ байт = __ бит, б) __ Кбайт = __ байт = 12288 бит; в) __ Кбайт = __ байт = 2 13 бит; г) __Гбайт =1536 Мбайт = __ Кбайт; д) 512 Кбайт = 2__ байт = 2__ бит.

Решение.
а) 5 Кбайт = 5120 байт =40 960 бит,
б) 1,5 Кбайт = 1536 байт = 12 288 бит;
в) 1 Кбайт = 2 10 байт = 2 13 бит;
г) 1,5 Гбайт = 1536 Мбайт = 1 572 864 Кбайт;
д) 512 Кбайт = 2 19 байт = 2 22 бит.

Пример 6. Какова мощность алфавита, с помощью которого записано сообщение, содержащее 2048 символов, если его объем составляет 1/512 часть одного мегабайта?

Решение.
1) 1/512 Мб * 1024 = 2 Кб * 1024 = 2048 байт
2) К = 2048 символов, следовательно, i = 1 байт = 8 бит
3) 2 i = N; 2 8 = 256 символов

Ответ: 1) 1/512 Мб * 1024 = 2 Кб * 1024 = 2048 байт
2) К = 2048 символов, следовательно, i = 1 байт = 8 бит
3) 2 i = N; 2 8 = 256 символов.

Решение.
Мощность компьютерного алфавита равна 256. Один символ несет 1 байт информации.
Значит, страница содержит 40*60=2400 байт информации. Объем всей информации в книге: 2400*150 = 360 000 байт.
Ответ: 360 000 байт.

Пример 8. Для передачи секретного сообщения используется код, состоящий из десяти цифр. При этом все цифры кодируются одним и тем же (минимально возможным) количеством бит. Определите информационный объем сообщения длиной в 150 символов.

Пример 9.В кодировке Unicode на каждый символ отводится два байта. Определите информационный объем слова из двадцати четырех символов в этой кодировке.

Решение.
I= K*i; I = 24*2 байт = 48 байт = 48*8бит = 384 бит.
Ответ: 384 бита.

Пример 10.В рулетке общее количество лунок равно 128. Какое количество информации мы получаем в зрительном сообщения об остановке шарика в одной из лунок?

Источник

Технология разработки экспертных систем

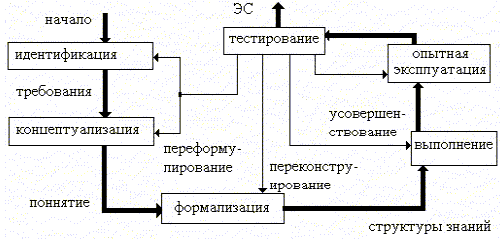
Технология их разработки ЭС, включает в себя шесть этапов (рис.5): этапы идентификации, концептуализации, формализации, выполнения, тестирования, опытной эксплуатации. Рассмотрим более подробно последовательности действий, которые необходимо выполнить на каждом из этапов.

1) На этапе идентификации необходимо выполнить следующие действия:

определить задачи, подлежащие решению и цели разработки,

определить экспертов и тип пользователей.

2) На этапе концептуализации:

проводится содержательный анализ предметной области,

выделяются основные понятия и их взаимосвязи,

определяются методы решения задач.

3) На этапе формализации:

выбираются программные средства разработки ЭС,

определяются способы представления всех видов знаний,

формализуются основные понятия.

4) На этапе выполнения (наиболее важном и трудоемком) осуществляется наполнение экспертом БЗ, при котором процесс приобретения знаний разделяют:

на «извлечение» знаний из эксперта,

на организацию знаний, обеспечивающую эффективную работу ЭС,

на представление знаний в виде, понятном для ЭС.

Процесс приобретения знаний осуществляется инженером по знаниям на основе деятельности эксперта.

5) На этапе тестирования эксперт и инженер по знаниям с использованием диалоговых и объяснительных средств проверяют компетентность ЭС. Процесс тестирования продолжается до тех пор, пока эксперт не решит, что система достигла требуемого уровня компетентности.

6) На этапе опытной эксплуатации проверяется пригодность ЭС для конечных пользователей. По результатам этого этапа возможна существенная модернизация ЭС.

Процесс создания ЭС не сводится к строгой последовательности этих этапов, так как в ходе разработки приходится неоднократно возвращаться на более ранние этапы и пересматривать принятые там решения.

Количество информации в случае различных вероятностей событий определяется по формуле Шеннона:

Существует множество ситуаций, когда возможные события имеют различные вероятности реализации. Рассмотрим примеры таких событий.

1. При случайном падении бутерброда вероятность падения его маслом вниз (более тяжёлой стороной) больше, чем маслом вверх.

2. В коробке 20 карандашей, из них 15 красных и 5 чёрных. Вероятность вытащить наугад красный карандаш больше, чем чёрный.

Количество информации в сообщении о некотором событии зависит от его вероятности. Чем меньше вероятность события, тем больше информации оно несёт.
P = K/N, где К – количество случаев реализации одного из исходов события, N – общее число возможных исходов одного из событий 2 i = log₂(1/p), где i – количество информации, p – вероятность события

Задача 1.В коробке 50 шаров, из них 40 белых и 10 чёрных. Определить количество информации в сообщении о вытаскивании наугад белого шара и чёрного шара.

Вероятность вытаскивания чёрного шара P₂ = 10/50 = 0,2

Количество информации о вытаскивании белого шара i₁ = log2(1/0,8) = log21,25

= log1,25/log2 » 0,32 бит

Количество информации о вытаскивании чёрного шара i₂ = log2(1/0,2) = log25 = log5/log2 » 2,32 бит

Ответ: 0,32 бит; 2,32 бит

Решение:События поимки карася или окуня не являются равновероятными, так как окуней в озере меньше, чем карасей.

Общее количество карасей и окуней в пруду 1500 + 500 = 2000.

Вероятность попадания на удочку карася

p₁ = 1500/2000 = 0,75, окуня p₂ – 500/2000 = 0,25.

I₁ = log₂(1/p1), I₁ = log2(1/p2), где I₁ и I₂ – вероятности поймать карася и окуня соответственно.

I₁ = log₂(1 / 0,75) » 0,43 бит, I₂ = log₂(1 / 0,25) » 2 бит – количество информации в сообщении поймать карася и поймать окуня соответственно.

Количество информации в сообщении поймать рыбу (карася или окуня) рассчитывается по формуле Шеннона

Ответ: в сообщении содержится 0,6 бит информации

Дата добавления: 2015-12-26 ; просмотров: 2249 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Логарифмом числа а по основанию b называется показатель степени, в которую надо возвести число a, чтобы получить число b

a log _a b = b, a > 0, b > 0, a ≠ 1

Вычисление логарифмов чисел по основанию 2 с помощьюэлектронного калькулятора

log ₂ 6 = log 6 / log 2, где log 6 и log 2 – десятичные логарифмы

Количество информации в случае различных вероятностей событий определяется по формуле:
Формула Шеннона: (американский учёный, 1948 г.)

где Pi – вероятность i-го события, N – количество возможных событий

Решение.
События поимки карася или окуня не являются равновероятными, так как окуней в озере меньше, чем карасей.

Общее количество карасей и окуней в пруду 1500 + 500 = 2000.
Вероятность попадания на удочку карася

p₁ = 1500/2000 = 0,75, окуня p₂ – 500/2000 = 0,25.

I₁ = log2(1/p1), I₁ = log2(1/p2), где I₁ и I₂ – вероятности поймать карася и окуня соответственно.

I₁ = log2(1 / 0,75) » 0,43 бит, I₂ = log2(1 / 0,25) » 2 бит – количество информации в сообщении поймать карася и поймать окуня соответственно.

Количество информации в сообщении поймать рыбу (карася или окуня) рассчитывается по формуле Шеннона

Ответ: в сообщении содержится 0,6 бит информации

Отчет

Отчет должен быть оформлен в текстовом редакторе и содержать:

¾ последовательность выполнения работы;

¾ ответы на контрольные вопросы;

¾ вывод о проделанной работе.

Контрольные вопросы

1. Какое количество информации несет в себе жесткий диск емкостью 4 терабайта, если производитель рассчитывает 1000 за 1024?

2. Чем отличается вероятностный подход к измерению информации от алфавитного?

3. Какие единицы измерения информации используют для флэш-накопителей?

Практическое занятие № 3

Тема программы: Способы измерения информации.

Тема: Скорость передачи информации.

Цель: научиться измерять и вычислять скорость передачи информацию.

Время выполнения: 2 часа

Раздаточный материал: дидактический материал

Программное обеспечение: операционная система, текстовый редактор.

Скорость передачи информации определяется количеством элементов двоичной информации,, передаваемых за 1 с. В синхронной передачи данных по коммутируемым каналам рекомендуется использовать скорости из следующего ряда: 600, 1200, 2400, 4800, 9600 бит/с. Для асинхронной передачи по коммутьируемым каналм рекомегндуется скорость 300 бит/с.

В синхронной передачи данных по арендованным каналам рекомендуется использовать скорости из следующих рядов:

а) предпочтительные: 600, 1200, 2400, 4800, 9600, 14400 бит/с;

б) дополнительные: 3000, 6000, 7200, 12000 бит/с;

в) допустимого диапазона: Nx600 бит/с (1

Одной из основных характеристик модема является скорость модуляции (modulation speed), которая определяет физическую скорость передачи данных без учета исправления ошибок и сжатия данных. Единицей измерения этого параметра является количество бит в секунду (бит/с), называемое бодом.

Любой канал связи имеет ограниченную пропускную способность (скорость передачи информации), это число ограничивается свойствами аппаратуры и самой линии (кабеля).

Объем переданной информации вычисляется по формуле Q=q*t, где q – пропускная способность канала (в битах в секунду), а t – время передачи

Пример 1. Скорость передачи данных через ADSL-соединение равна 128000 бит/c. Через данное соединение передают файл размером 625 кбайт. Определить время передачи файла в секундах.

1) выделим в заданных больших числах степени двойки и переведем размер файла в биты, чтобы «согласовать» единиц измерения:

128000 бит/c = 128 · 1000 бит/с = 27 · 125 · 8 бит/с = 27 · 53 · 23 бит/с = 210·53 бит/с

625 кбайт = 54 кбайт = 54 · 213 бит.

2) чтобы найти время передачи в секундах, нужно разделить размер файла на скорость передачи:

t=(54 · 213)бит / 210·53 бит/с = 40 с.

Пример 2. Скорость передачи данных через ADSL-соединение равна 512000 бит/c. Передача файла через это соединение заняла 1 минуту. Определить размер файла в килобайтах.

1) выделим в заданных больших числах степени двойки; переведем время в секунды (чтобы «согласовать» единицы измерения), а скорость передачи – в кбайты/с, поскольку ответ нужно получить в кбайтах:

1 мин = 60 с = 4 · 15 с = 22 · 15 с

512000 бит/c = 512 · 1000 бит/с = 29 · 125 · 8 бит/с = 29 · 53 · 23 бит/с = 212 · 53 бит/с = 29 · 53 бит/с = (29 · 53) / 210 кбайт/с = (53 / 2) кбайт/с

2) чтобы найти объем файла, нужно умножить время передачи на скорость передачи:

Q=q*t = 22 · 15 с *(53 / 2) кбайт/с = 3750 кбайт

Пример 3. C помощью модема установлена связь с другим компьютером со скоростью соединения 19200, с коррекцией ошибок и сжатием данных.
а) Можно ли при таком соединении файл размером 2,6 килобайт передать за 1 секунду? Обоснуйте свой ответ.
б) Всегда ли при таком соединении файл размером 2,3 килобайт будет передаваться за 1 секунду? Обоснуйте свой ответ.
в) Можно ли при таком соединении оценить время передачи файла размером 4 Мб? Если можно, то каким образом?

Каждая из реализаций С₁, С₂,….С_i,…С_m будет иметь определенную вероятность появления в эксперименте по наблюдению реализаций. Тогда неопределенность (энтропия) и количество информации в реализации (в среднем по всем реализациям) определяются равенством

Энтропия и количество информации на одну степень свободы (на одну выборку) равны

Избыточностьпоказывает, какая доля максимально возможной при заданном объеме алфавита неопределенности не используется источником.

Где Н_u – энтропия рассматриваемого источника, Н_max – максимально возможное значение его энтропии, которое может быть достигнуто подбором распределения и ликвидацией взаимозависимости элементов алфавита. Так, для дискретного источника с М элементами

Выполнение расчетных задач

Задача №1

Доказать, что H(x,y)≤H(x)+H(y).

Решение:

По определению, .

Для статистически зависимых событий .

— это частная энтропия Y при условии, что известно состояние X=x_i.

Наличие информации о состоянии X не может увеличить неопределенность состояния Y, но может уменьшить его в случае зависимости Y от X. Значит, условная энтропия не больше безусловной энтропии , то есть . Тогда средняя условная энтропия ,

то есть .

Значит,

Задача №2

Показать, что для регулярной марковской цепи энтропия H(x) ( r ) за r шагов равняется энтропии за один шаг, умноженной на число шагов r.

Решение:

Регулярная цепь Маркова полностью характеризуется матрицей переходных вероятностей и предельным стационарным распределением вероятностей состояний .

В стационарном режиме энтропия за один шаг не зависит от номера шага и равна ,

— стационарная вероятность k-го состояния,

— энтропия в k-м состоянии.

Энтропия за r шагов равна сумме энтропий за каждый шаг. Так как энтропия за каждый шаг одинакова, то сумма энтропий равна .

Задача №3

Вычислить энтропию H_д(x) распределения p_x(x) изображенного на рисунке.

Построить график зависимости H_д(x) в функции параметра d.

Решение:

Из условия нормировки .

Плотность данного распределения

Дифференциальная энтропия

.

Задача 4

Ответ: 4.86 бита

Начальное распределение вероятностей углов курсов самолетов равномерное в интервале от до с плотностью вероятности .

Дифференциальная энтропия этого распределения

бит.

Конечное распределение вероятностей углов курсов самолетов нормальное с параметрами и плотностью вероятности .

Дифференциальная энтропия этого распределения

Изменение энтропии бит.

Энтропия уменьшилась на 4,86 бит.

Задача 5

Измерительное устройство вырабатывает вре­менные интервалы, распределенные случайным образом в пределах от 100 до 500 мс. Как изменится энтропия случайной величины при изменении точности измерения с 1 мс до 1 мкс?

Источник