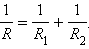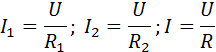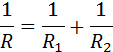В параллельной цепи с более чем одним проводником полное сопротивление цепи

В параллельной цепи с более чем одним проводником полное сопротивление цепи

Проводники в электрических цепях могут соединяться последовательно и параллельно.

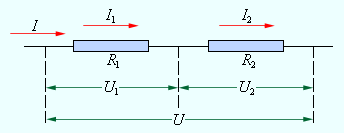
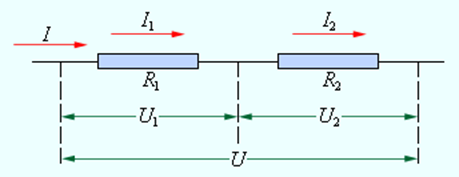
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:

По закону Ома, напряжения и на проводниках равны

Общее напряжение на обоих проводниках равно сумме напряжений ₁ и ₂:

где – электрическое сопротивление всей цепи. Отсюда следует:

При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.

Этот результат справедлив для любого числа последовательно соединенных проводников.

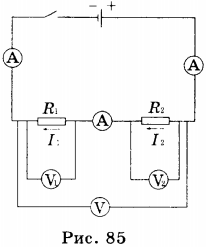
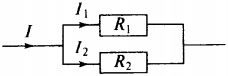
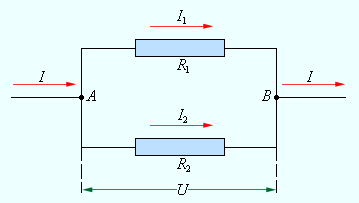
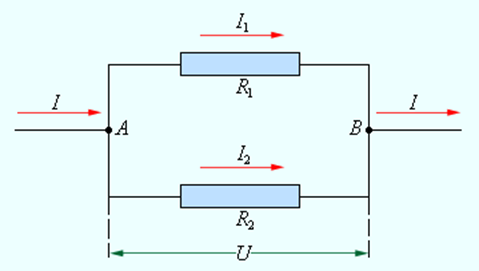
При параллельном соединении (рис. 1.9.2) напряжения ₁ и ₂ на обоих проводниках одинаковы:

Сумма токов ₁ + ₂, протекающих по обоим проводникам, равна току в неразветвленной цепи:

Этот результат следует из того, что в точках разветвления токов (узлы и ) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу за время Δ подтекает заряд Δ, а утекает от узла за то же время заряд ₁Δ + ₂Δ. Следовательно, = ₁ + ₂.

Записывая на основании закона Ома

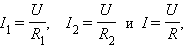где – электрическое сопротивление всей цепи, получим

При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Этот результат справедлив для любого числа параллельно включенных проводников.

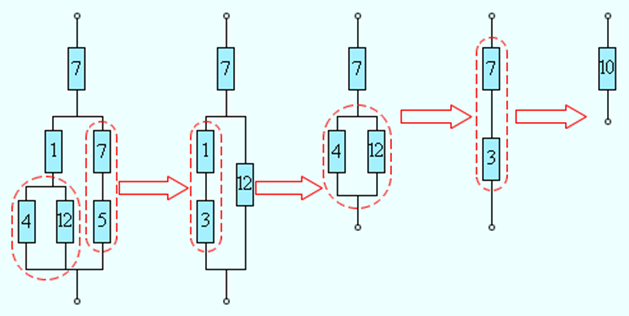
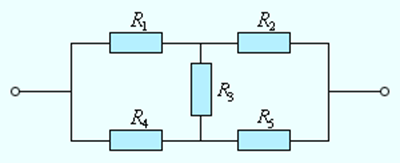
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.

Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.

Цепи, подобные изображенной на рис. 1.9.4, а также цепи с разветвлениями, содержащие несколько источников, рассчитываются с помощью правил Кирхгофа.

Источник

Последовательное и параллельное соединения проводников

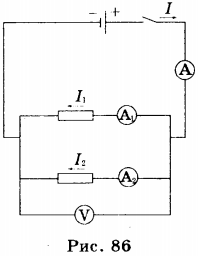
1. Потребители электрической энергии: электрические лампочки, резисторы и пр. — могут по-разному соединяться друг с другом в электрической цепи. Существует два основных типа соединения проводников: последовательное и параллельное. При последовательном соединении проводников конец одного проводника соединяется с началом другого проводника, а его конец — с началом третьего и т.д. (рис. 85).

Примером последовательного соединения проводников может служить соединение электрических лампочек в ёлочной гирлянде.

При последовательном соединении проводников ток проходит через все лампочки, при этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд, т.е. заряд не скапливается ни в какой части проводника. Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова: ​ \( I_1=I_2=I \) ​.

Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений: ​ \( R_1=R_2=R \) ​. Это следует из того, что при последовательном соединении проводников их общая длина увеличивается, она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.

По закону Ома напряжение на каждом проводнике равно: ​ \( U_1=IR_1 \) ​, ​ \( U_2=IR_2 \) ​, а общее напряжение равно ​ \( U=I(R_1+R_2) \) ​. Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике: ​ \( U=U_1+U_2 \) ​.

Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.

2. Примером параллельного соединения проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.

При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи (А), а вторым концом к другой точке цепи (В) (рис. 86).

Поэтому вольтметр, подключенный к этим точкам, покажет напряжение как на проводнике 1, так и на проводнике 2. Таким образом, напряжение на концах всех параллельно соединённых проводников одно и то же: ​ \( U_1=U_2=U \) ​.

При параллельном соединении проводников электрическая цепь разветвляется, в данном случае в точке В. Поэтому часть общего заряда проходит через один проводник, а часть — через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: ​ \( I=I_1+I_2 \) ​.

При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление ​ \( r \) ​, то их общее сопротивление равно: ​ \( R=r/2 \) ​. Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения, соответственно уменьшается сопротивление.

Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно: они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них и соответствие суммарной силы тока предельно допустимой силе тока.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. На рисунке изображёна схема участка электрической цепи АВ. В эту цепь параллельно включены два резистора сопротивлением ​ \( R_1 \) ​ и ​ \( R_2 \) ​. Напряжения на резисторах соответственно ​ \( U_1 \) ​ и ​ \( U_2 \) ​.

По какой из формул можно определить напряжение U на участке АВ?

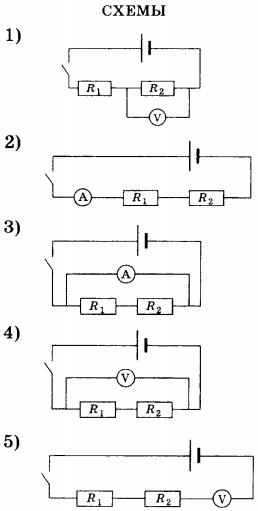
2. На рисунке изображёна схема электрической цепи, содержащая два параллельно включённых резистора сопротивлением ​ \( R_1 \) ​ и ​ \( R_2 \) ​. Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?

1) ​ \( I=I_1=I_2 \) ​
2) \( I=I_1+I_2 \)
3) \( U=U_1+U_2 \)
4) \( R=R_1+R_2 \)

3. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением R> и R2. Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?

4. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением ​ \( R_1 \) ​ и ​ \( R_2 \) ​. Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?

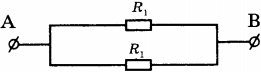
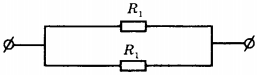
5. На рисунке изображена схема электрической цепи. В эту цепь параллельно включены два одинаковых резистора сопротивлением ​ \( R_1 \) ​. По какой из формул можно определить общее сопротивление цепи ​ \( R \) ​?

6. Общее сопротивление участка цепи, изображённого на рисунке, равно 9 Ом. Сопротивления резисторов ​ \( R_1 \) ​ и ​ \( R_2 \) ​ равны. Чему равно сопротивление каждого резистора?

1) 81 Ом
2) 18 Ом
3) 9 Ом
4) 4,5 Ом

7. Чему равно сопротивление участка цепи, содержащего три последовательно соединенных резистора сопротивлением по 9 Ом каждый?

1) 1/3 Ом
2) 3 Ом
3) 9 Ом
4) 27 Ом

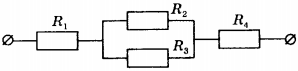
8. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если ​ \( R_1 \) ​ = 1 Ом, ​ \( R_2 \) ​ = 10 Ом, ​ \( R_3 \) ​ = 10 Ом, ​ \( R_4 \) ​ = 5 Ом?

1) 9 Ом
2) 11 Ом
3) 16 Ом
4) 26 Ом

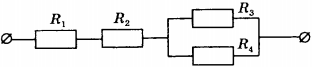
9. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если \( R_1 \) = 1 Ом, \( R_2 \) = 3 Ом, \( R_3 \) = 10 Ом, \( R_4 \) = 10 Ом?

1) 9 Ом
2) 10 Ом
3) 14 Ом
4) 24 Ом

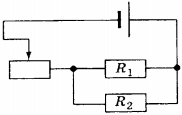
10. Если ползунок реостата (см. схему) переместить влево, то сила тока

1) в резисторе ​ \( R_1 \) ​ уменьшится, а в резисторе ​ \( R_2 \) ​ увеличится
2) увеличится в обоих резисторах
3) в резисторе ​ \( R_1 \) ​ увеличится, а в резисторе ​ \( R_2 \) ​ уменьшится
4) уменьшится в обоих резисторах

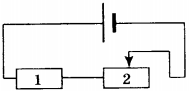
11. На рисунке изображена электрическая цепь, состоящая из источника тока, резистора и реостата. Как изменяются при передвижении ползунка реостата вправо его сопротивление, сила тока в цепи и напряжение на резисторе 1?

Для каждой физической величины определите соответствующий характер изменения. Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) сопротивление реостата 2
Б) сила тока в цепи
B) напряжение на резисторе 1

ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличивается
2) уменьшается
3) не изменяется

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) сила тока в резисторе \( R_1 \) ​ и \( R_2 \)
Б) напряжение на резисторе \( R_2 \)
B) общее напряжение на резисторах \( R_1 \) ​ и \( R_2 \)

Часть 2

13. Три резистора соединены, как показано на рисунке. Сопротивления резисторов ​ \( R_1 \) ​ = 10 Ом, \( R_2 \) = 5 Ом, \( R_3 \) = 5 Ом. Каково напряжение на резисторе 1, если амперметр показывает силу тока 2 А?

Источник

Последовательное и параллельное соединение проводников

Последовательное соединение проводников

Проводники в электрических цепях могут соединяться как последовательным, так и параллельным способами.

Опираясь на закон Ома, можно заявить, что напряжения U 1 и U 2 на проводниках равняются следующим выражениям:

Общее напряжение U на обоих проводниках эквивалентно сумме напряжений U 1 и U 2 :

где R является электрическим сопротивлением всей цепи.

Из этого следует, что общее сопротивление R равняется сумме сопротивлений на входящих в данную цепь отдельных проводников:

Данный результат применим для любого количества последовательно соединенных проводников.

Параллельное соединение проводников

Совокупность существующих в обоих проводниках токов I 1 + I 2 равняется значению тока в неразветвленной цепи, то есть:

Опираясь на закон Ома, запишем для каждой ветви:

где R является электрическим сопротивлением всей цепи, получим

В условиях параллельного соединения проводников обратная общему сопротивлению цепи величина, равняется сумме величин, обратных сопротивлениям параллельно включенных проводников.

Полученный вывод может быть применим для любого количества включенных параллельно проводников.

Применение формул для расчета сопротивления сложной цепи

Источник

Последовательное и параллельное соединение проводников

Проводники в электрических цепях могут соединяться последовательно и параллельно.

При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:

Последовательное соединение проводников

По закону Ома, напряжения U₁ и U₂ на проводниках равны

Общее напряжение U на обоих проводниках равно сумме напряжений U₁ и U₂:

где R – электрическое сопротивление всей цепи. Отсюда следует:

При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.

Этот результат справедлив для любого числа последовательно соединенных проводников.

При параллельном соединении (рис. 1.9.2) напряжения U₁ и U₂ на обоих проводниках одинаковы:

Сумма токов I₁ + I₂, протекающих по обоим проводникам, равна току в неразветвленной цепи:

Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I₁Δt + I₂Δt. Следовательно, I = I₁ + I₂.

Параллельное соединение проводников

Записывая на основании закона Ома

где R – электрическое сопротивление всей цепи, получим

При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Этот результат справедлив для любого числа параллельно включенных проводников.

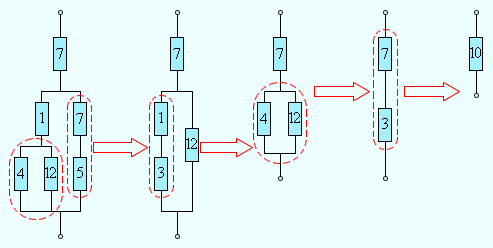
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.

Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны в омах (Ом)

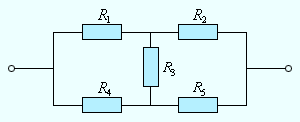
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.

Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников

Цепи, подобные изображенной на рис. 1.9.4, а также цепи с разветвлениями, содержащие несколько источников, рассчитываются с помощью правил Кирхгофа.

Источник

Параллельное и последовательное соединение проводников.

Для параллельного соединения проводников справед­ливы следующие соотношения:

а) электрический ток, поступающий в точку А разветвления проводников (она называется также узлом), равен сумме токов в каждом из элементов цепи:

б) напряжение U на концах проводников, соединенных параллельно, одно и то же:

в) при параллельном соединении проводников складываются их обратные сопротивления:
г) сила тока и сопротивление в проводниках связаны соотношением:

.

Для последовательного соединения проводников в цепи справедливы следующие соотношения:

.

а) для общего тока I:

где I₁ и I ₂ — ток в проводниках 1 и 2 соответственно; т. е. при последовательном соединении про­водников сила тока на отдельных участках цепи одинакова;

б) общее напряжение U на концах всего рассматриваемого участка равно сумме напряжений на отдельных его участках:

в) полное сопротивление R всего участка цепи равно сумме последовательно соединенных сопротивлений:

г) также справедливо соотношение:

.

Источник