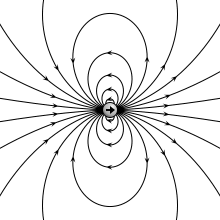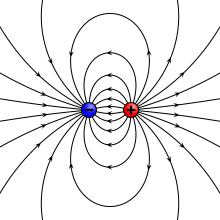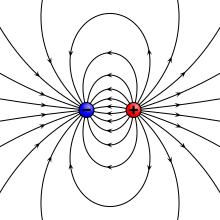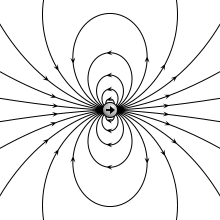
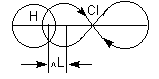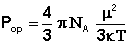дипольный момент в чем измеряется

Дипольный момент в чем измеряется

Виктор Александрович КОГАН
профессор, заведующий кафедрой физической и коллоидной химии
Ростовского Государственного Университета

ИЗБРАННЫЕ ЛЕКЦИИ ПО КУРСУ «МЕТОДЫ ИССЛЕДОВАНИЯ КООРДИНАЦИОННЫХ СОЕДИНЕНИЙ»

Метод дипольных моментов в химии

Лекция посвящена одному из важнейших физических методов исследования строения вещества – методу дипольных моментов. Рассмотрена природа дипольного момента и методы его определения, а также приведены отдельные примеры применения метода дипольных моментов для выяснения строения химических соединений.

1. Общие представления о природе дипольного момента

Дипольный момент – важная молекулярная константа, характеризующая электрическую симметрию молекулы.

Знание величины дипольного момента необходимо для изучения природы химической связи, оценки прочности донорно-акцепторных и межмолекулярных связей, для квантово-химических расчетов. По величине дипольного момента можно судить об изомерии и конформации органических соединений, конфигурации координационных узлов комплексов, о взаимном влиянии атомов и связей в молекуле.

Величина электрического дипольного момента (μ) определяется соотношением:

(1)

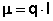
Причиной появления дипольного момента являются несколько факторов. В первую очередь – это различия в природе составляющих молекулу атомов. В простейшем случае для двухатомной молекулы μ = 0, если она состоит из двух одинаковых атомов. Это относится к H₂, O₂, N₂ и т.д. В двухатомной молекуле с атомами разной природы проявляется постоянный дипольный момент, т. к., вследствие разной электроотрицательности, характеризующей способность атома оттягивать электронную плотность, появляется асимметрия электронной плотности. Другие причины – разные гибридные состояния орбиталей атомов. Так, например, для связи H-Cl, образованной 1s-орбиталью водорода и 3p-орбиталью хлора, вследствие различной формы s- и p-орбиталей, центр тяжести заряда перекрывания смещен в сторону водорода на ΔL, за счет чего возникает дополнительный, т. н. гомеополярный дипольный момент (рис.1):

Рис. 1. Схема происхождения гомеополярного диполя.

Естественно, молекулы HCl, HBr, HI имеют постоянные дипольные моменты, равные, соответственно, 1.95 D, 0.79 D, 0.40 D. Другие вклады в суммарный дипольный момент возникают из-за асимметрии связывающей и несвязывающей атомных орбиталей вследствие их гибридизации. Так, дипольный момент аммиака, 1.46 D, в основном обусловлен моментом несвязывающей пары электронов азота.

2. Методы определения дипольных моментов

Из всех методов получили наиболее широкое распространение методы определения дипольных моментов, основанные на измерении диэлектрической проницаемости (ε) вещества. Этими методами измерены дипольные моменты молекул более 10000 веществ. Переход от измеряемого значения ε газа, чистой жидкости или разбавленного раствора, т.е. макроскопической характеристики диэлектрика, к величине дипольного момента основан на теории поляризации диэлектриков. Считается, что при наложении электрического поля на диэлектрик его полная поляризация Р складывается из наведенной или индуцированной поляризации Р_м и поляризации Р_ор и связана с μ уравнением Ланжевена-Дебая (2).

(2)

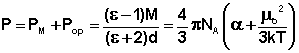
Измерения диэлектрической проницаемости проводят в постоянном поле или при низких частотах, обеспечивающих полную ориентацию молекул по полю. Кратко остановимся на типичной процедуре определения μ_о в разбавленных растворах. Она основана на предположении об аддитивности свойств составляющих раствор компонентов:

(3)

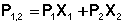
где Р_1,2, Р₁, Р₂ – молекулярные поляризации раствора, растворителя и растворенного вещества соответственно;
Х₁, Х₂ – мольные доли растворителя и растворенного вещества.

С учетом уравнения (2) уравнение (3) для раствора будет выглядеть как (4):

(4)

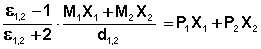
где М₁ и М₂ – молекулярные веса растворителя и растворенного вещества;
ε_1,2 – диэлектрическая проницаемость раствора;
d_1,2 – плотность раствора.

Из уравнения (4) можно вычислить Р₂ – молекулярную поляризацию растворенного вещества. В этом методе допускается, что молекулы полярного вещества могут вести себя в растворах как в парообразном состоянии и свободно ориентироваться в приложенном поле только для бесконечно разбавленных растворов, поэтому значение Р₂ следует экстраполировать на нулевую концентрацию (Х₂ = 0) и найти значение молекулярной поляризации растворенного вещества при бесконечном разбавлении (Р_2∞).

Эксперимент сводится к измерению диэлектрической проницаемости и плотности 5-7 разбавленных растворов исследуемого соединения при точно поддерживаемой температуре (обычно 25 °С) в интервале концентраций растворенного вещества от 0,001¸ 0,01 мольных долей. Выбор интервала концентраций зависит от растворимости и полярности вещества и может колебаться в сторону уменьшения мольных долей для более полярных соединений. Затем по формуле (4) находят значение молекулярной поляризации растворенного вещества для каждой концентрации и по полученным данным строят кривую зависимости Р₂ от концентраций, по которой экстраполируют Р₂ до нулевой концентрации и находят значение Р_2∞. Эту величину можно также получить, используя различные приемы экстраполяции к нулевой концентрации для диэлектрической проницаемости и плотности.

Величину дипольного момента рассчитывают из уравнения Дебая (2)

из которого, подставляя значения N, κ, π, можно вычислить величину постоянного дипольного момента по формуле (5):

, эл.-ст. ед. (5)

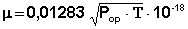
Найденное в эксперименте значение Р_2∞ включает в себя электронную (Р_эл) и атомную (Р_ат) молекулярные поляризации и поэтому Р_ор в уравнении (5) вычисляется как Р_ор = Р_2∞ – Р_ат – Р_эл.

Р_эл считают равной рефракции вещества, которое вычисляется по той же схеме аддитивности на основании измерения коэффициентов преломления и плотности той же серии растворов, а Р_ат вследствие ее малости очень часто пренебрегают. Следует отметить, что Р_эл можно рассчитать по рефракциям связей и групп, если не требуется высокая точность в значении дипольного момента.

Сходимость результатов, полученных различными методами при корректном использовании правильных расчетных формул бывает достаточно хорошей, как показано в табл. 1:

Таблица 1. Дипольные моменты молекул (в D)

Источник

Электрический дипольный момент

Классическая электродинамика

Электричество · Магнетизм

Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток Известные учёные Генри Кавендиш Майкл Фарадей Никола Тесла Андре-Мари Ампер Густав Роберт Кирхгоф Джеймс Клерк (Кларк) Максвелл Генри Рудольф Герц Альберт Абрахам Майкельсон Роберт Эндрюс Милликен

См. также: Портал:Физика

Электри́ческий ди́польный моме́нт — векторная физическая величина, характеризующая, наряду с суммарным зарядом (и реже используемыми высшими мультипольными моментами), электрические свойства системы заряженных частиц (распределения зарядов) в смысле создаваемого ею поля и действия на нее внешних полей. Главная после суммарного заряда и положения системы в целом (ее радиус-вектора) характеристика конфигурации зарядов системы при наблюдении ее издали.

Дипольный момент — первый [прим 1] мультипольный момент.

Простейшая система зарядов, имеющая определенный (не зависящий от выбора начала координат) ненулевой дипольный момент — это диполь (две точечные частицы с одинаковыми по величине разноимёнными зарядами). Электрический дипольный момент такой системы по модулю равен произведению величины положительного заряда на расстояние между зарядами и направлен от отрицательного заряда к положительному, или:

— где q — величина положительного заряда, — вектор с началом в отрицательном заряде и концом в положительном.

Для системы из N частиц электрический дипольный момент равен

где — заряд частицы с номером а — её радиус-вектор; или, если суммировать отдельно по положительным и отрицательным зарядам:

Электрический дипольный момент нейтральной системы зарядов не зависит от выбора начала координат, а определяется относительным расположением (и величинами) зарядов в системе.

Из определения видно, что дипольный момент аддитивен (дипольный момент наложения нескольких систем зарядов равен просто векторной сумме их дипольных моментов), а в случае нейтральных систем это свойство приобретает еще более удобную форму в силу изложенного в абзаце выше.

Дипольный момент ненейтральной системы зарядов, вычисленный по приведенному выше определению, может выбором начала координат быть сделан равным любому наперед заданному числу (например, нулю). Однако и в этом случае, если мы хотим избежать такого произвола, при желании может быть использована какая-нибудь процедура внесения однозначности (которая будет тоже представлять собой предмет произвольного условного соглашения, но всё же будет формально фиксирована).

Но и при произвольном выборе начала координат (ограничивающемся тем условием, чтобы начало координат находилось внутри данной системы зарядов или по крайней мере близко от нее, и уж во всяком случае не попадая в ту область, в которой мы вычисляем дипольную поправку к полю единственного точечного заряда или дипольный член мультипольного разложения) все вычисления (дипольной поправки к потенциалу или напряженности поля, создаваемого системой, действующий на нее со стороны внешнего поля вращающий момент или дипольная поправка к потенциальной энергии системы во внешнем поле) проходят успешно.

Интересной иллюстрацией мог бы быть следующий пример:

Электрический дипольный момент (если он ненулевой) определяет в главном приближении электрическое [прим 3] поле диполя (или любой ограниченной системы с суммарным нулевым зарядом) на большом расстоянии от него, а также воздействие на диполь внешнего электрического поля.

Физический и вычислительный смысл дипольного момента состоит в том, что он дает поправки первого порядка (чаще всего — малые) в положение каждого заряда системы по отношению к началу координат (которое может быть условным, но приближенно характеризует положение системы в целом — система при этом подразумевается достаточно компактной). Эти поправки входят в него в виду векторной суммы, и везде, где при вычислениях такая конструкция встречается (а в силу принципа суперпозиции и свойства сложения линейных поправок — см.Полный дифференциал — такая ситуация встречается часто), там в формулах оказывается дипольный момент.

Содержание

Электрическое поле диполя

Напряжённость электрического поля и электрический потенциал неподвижного или медленно движущегося диполя (или в целом нейтральной системы зарядов, имеющей ненулевой дипольный момент) с электрическим дипольным моментом на больших расстояниях в главном приближении выражается как:

в СГСЭ: в СИ:

где — единичный вектор из центра диполя в направлении точки измерения, а точкой обозначено скалярное произведение.

Достаточно просты выражения (в том же приближении, тождественно совпадающие с формулами, приведенными выше) для продольной (вдоль радус-вектора, проведенного от диполя в данную точку) и поперечной компонент напряженности электрического поля:

где — угол между направлением вектора дипольного момента и радиус-вектором в точку наблюдения (формулы приведены в системе СГС; в СИ аналогичные формулы отличаются только множителем ). Третья компонента напряженности электрического поля — ортогональная плоскости, в которой лежат вектор дипольного момента и радиус-вектор, — всегда равна нулю.

Действие поля на диполь

Об условиях корректности приближенных (в общем случае) формул данного параграфа — см.ниже.

Единицы измерения электрического дипольного момента

Системные единицы измерения электрического дипольного момента не имеют специального названия. В СИ это просто Кл·м.

Электрический дипольный момент молекул принято измерять в дебаях:

1 Д = 10 −18 единиц СГСЭ момента электрического диполя, 1 Д = 3,33564·10 −30 Кл·м.

Поляризация

Дипольный момент единицы объема (поляризованной) среды (диэлектрика) называется вектором поляризации (см. Поляризация).

Дипольный момент элементарных частиц

Многие экспериментальные работы посвящены поиску электрического дипольного момента (ЭДМ) фундаментальных и составных элементарных частиц, а именно электронов и нейтронов. Поскольку ЭДМ нарушает как пространственную (Р), так и временну́ю (T) чётность, его значение даёт (при условии ненарушенной СРТ-симметрии) модельно-независимую меру нарушения CP-симметрии в природе. Таким образом, значения ЭДМ дают сильные ограничения на масштаб CP-нарушения, которое может возникать в расширениях Стандартной Модели физики элементарных частиц.

Действительно, многие теории, несовместимые с существующими экспериментальными пределами на ЭДМ частиц, уже были исключены. Стандартная Модель (точнее, её сектор — квантовая хромодинамика) сама по себе разрешает гораздо большее значение ЭДМ нейтрона (около 10 −8 дебая), чем эти пределы, что привело к так называемой сильной CP-проблеме и вызвало поиски новых гипотетических частиц, таких как аксион.

Текущее поколение экспериментов по поиску ЭДМ частиц достигает чувствительности в диапазоне, где могут проявляться эффекты суперсимметрии. Эти эксперименты дополняют поиск эффектов суперсимметрии на LHC.

Дипольное приближение

Дипольный член (определяемый дипольным моментом системы или распределения зарядов) является лишь одним из членов бесконечного ряда, называемого мультипольным разложением, дающего при полном суммировании точное значение потенциала или напряженности поля в точках, находящихся на конечном расстоянии от системы зарядов-источников. В этом смысле дипольный член выступает как равноправный с остальными, в том числе и высшими, членами мультипольного разложения (хотя зачастую он и может давать больший вклад в сумму, чем высшие члены). Этот взгляд на дипольный момент и дипольный вклад в создаваемое системой зарядов электрическое поле обладает существенной теоретической ценностью, но в деталях довольно сложен и довольно далеко выходит за рамки необходимого для понимания существенных физического смысла свойств дипольного момента и большинства областей его использования.

Для прояснения физического смысла дипольного момента, так же как и для большинства его приложений, достаточно ограничиться гораздо более простым подходом — рассматривать дипольное приближение.

Широкое использование дипольного приближения основывается на той ситуации, что очень во многих, в том числе теоретически и практически важных случаях можно не суммировать весь ряд мультипольного разложения, а ограничиться только низшими его членами — до дипольного включительно. Часто этот подход дает вполне удовлетворительную или даже очень маленькую погрешность.

Дипольное приближение для системы источников

В электростатике достаточное условие применимости дипольного приближения (в смысле задачи определения электрического потенциала или напряженности электрического поля, создаваемого системой зарядов, имеющей определенный суммарный заряд и определенный дипольный момент) описывается весьма просто: хорошим это приближение является для областей пространства, удаленных от системы-источника на расстояние r, много большее, чем характерный (а лучше — чем максимальный) размер d самой этой системы. Таким образом, для условий дипольное приближение r >> d является хорошим.

Если суммарный заряд системы равен нулю, а ее дипольный момент нулю не равен, дипольное приближение в своей области применимости является главным приближением, то есть в его области применимости оно описывает основной вклад в электрическое поле. Остальные же вклады при r >> d пренебрежимо малы (если только дипольный момент не оказывается слишком мал по сравнению с квадрупольным, октупольным или высшими мультипольными моментами).

Если суммарный заряд не равен нулю, главным становится монопольное приближение (нулевое приближение, закон Кулона в чистом виде), а дипольное приближение, являясь следующим, первым, приближением, может играть роль малой поправки к нему. Впрочем, в такой ситуации эта поправка будет очень мала в сравнении с нулевым приближением, если только мы находимся в области пространства, где вообще говоря само дипольное приближение является хорошим. Это несколько снижает его ценность в данном случае (за исключением, правда, ситуаций, описанных чуть ниже), поэтому главной областью применения дипольного приближения приходится признать случай нейтральных в целом систем зарядов.

Существуют ситуации, когда дипольное приближение является хорошим (иногда очень хорошим и в каких-то случаях даже может давать практически точное решение) и при невыполнении условия r >> d. Для этого нужно только чтобы высшие мультипольные моменты (начиная с квадрупольного) обращались в ноль или очень быстро стремились к нулю. Это довольно легко реализуется для некоторых распределенных систем. [прим 6]

В дипольном приближении, если суммарный заряд ноль, вся система зарядов, какой бы она ни была, если только ее дипольный момент не ноль, эквивалентна маленькому диполю (в этом случае всегда подразумевается маленький диполь) — в том смысле, что она создает поле, приближенно совпадающее с полем маленького диполя. В этом смысле любую такую систему отождествляют с диполем и к ней могут применяться термины диполь, поле диполя итд. В статье выше, даже если это не оговорено явно, всегда можно вместо слова диполь слова «нейтральная в целом система, имеющая ненулевой дипольный момент» — но, конечно, вообще говоря только в случае, если подразумевается выполнение условий корректности дипольного приближения.

Дипольное приближение для действия внешнего поля на систему зарядов

Идеально дипольное приближение для формул механического момента, создаваемого внешним полем, действующим на диполь, и потенциальной энергии диполя во внешнем поле, работает в случае однородности внешнего поля. В этом случае эти две формулы выполняются точно для любой системы, имеющей определенный дипольный момент, независимо от размера (равенство нулю суммарного ее заряда подразумевается).

Границу приемлемости дипольного приближения для этих формул определяет в целом такое условие: разность напряженности поля в разных точках системы должна быть по модулю много меньше самого значения напряженности поля. Качественно это означает, что для обеспечения корректности этих формул размеры системы должны быть тем меньше, чем более неоднородно действующее на нее поле.

Источник

Теоретически электрический диполь определяется членом первого порядка мультипольного разложения ; он состоит из двух равных и противоположных зарядов, бесконечно близких друг к другу, хотя реальные диполи имеют разделенный заряд.

СОДЕРЖАНИЕ

Элементарное определение

и направлена ​​от отрицательного заряда к положительному. Некоторые авторы могут разделить d пополам и использовать s = d / 2, поскольку эта величина представляет собой расстояние между любым зарядом и центром диполя, что приводит к коэффициенту два в определении.

Энергия и крутящий момент

На объект с электрическим дипольным моментом действует крутящий момент τ, когда он помещен во внешнее электрическое поле. Крутящий момент стремится выровнять диполь с полем. Диполь, расположенный параллельно электрическому полю, имеет меньшую потенциальную энергию, чем диполь, находящийся с ним под некоторым углом. Для пространственно однородного электрического поля E энергия U и крутящий момент определяются выражением τ <\ displaystyle <\ boldsymbol <\ tau>>>

Диполь, ориентированный параллельно или антипараллельно направлению увеличения неоднородного электрического поля (градиент поля), будет испытывать крутящий момент, а также силу в направлении своего дипольного момента. Можно показать, что эта сила всегда будет параллельна дипольному моменту независимо от со- или антипараллельной ориентации диполя.

Выражение (общий случай)

Это выражение эквивалентно предыдущему выражению в случае нейтральности заряда и N = 2. Для двух противоположных зарядов, обозначая расположение положительного заряда пары как r ₊ и расположение отрицательного заряда как r _— :

показывая, что вектор дипольного момента направлен от отрицательного заряда к положительному, поскольку вектор положения точки направлен наружу от начала координат к этой точке.

Дипольный момент особенно полезен в контексте общей нейтральной системы зарядов, например пары противоположных зарядов или нейтрального проводника в однородном электрическом поле. Для такой системы зарядов, представленной в виде массива пар противоположных зарядов, соотношение электрического дипольного момента выглядит следующим образом:

Потенциал и поле электрического диполя.

Идеальный диполь состоит из двух противоположных зарядов с бесконечно малым разделением. Мы вычисляем потенциал и поле такого идеального диполя, начиная с двух противоположных зарядов на расстоянии d> 0 и принимая предел при d → 0.

Два близко расположенных противоположных заряда ± q имеют потенциал вида:

где разделение зарядов:

Результат для дипольного потенциала также может быть выражен как:

который связывает дипольный потенциал с точечным зарядом. Ключевым моментом является то, что потенциал диполя падает быстрее с расстоянием R, чем потенциал точечного заряда.

Электрическое поле диполя представляет собой отрицательный градиент потенциала, приводящий к:

Таким образом, хотя два близко расположенных противоположных заряда не совсем идеальный электрический диполь (потому что их потенциал на коротких расстояниях не диполь), на расстояниях, намного больших, чем их разделение, их дипольный момент p появляется непосредственно в их потенциале и поле.

Плотность дипольного момента и плотность поляризации

Дипольный момент множества зарядов,

определяет степень полярности массива, но для нейтрального массива это просто свойство вектора массива без информации об абсолютном расположении массива. Дипольный момент плотность массива р ( г ) содержит как местоположение массива и его дипольный момент. Когда приходит время вычислить электрическое поле в некоторой области, содержащей массив, уравнения Максвелла решаются, и информация о массиве зарядов содержится в плотности поляризации P ( r ) уравнений Максвелла. В зависимости от того, насколько детально требуется оценка электрического поля, более или менее информация о массиве зарядов должна быть выражена через P ( r ). Как поясняется ниже, иногда достаточно точно взять P ( r ) = p ( r ). Иногда требуется более подробное описание (например, дополнение плотности дипольного момента дополнительной квадрупольной плотностью), а иногда даже более сложные версии P ( r ).

Формулировка уравнений Максвелла, основанная на разделении зарядов и токов на «свободные» и «связанные» заряды и токи, приводит к введению D- и P- полей:

с ρ _b в качестве связанного заряда, под которым понимается разница между полной и свободной плотностями заряда.

Кстати, в отсутствие магнитных эффектов уравнения Максвелла указывают, что

Предположим, что заряды разделены на свободные и связанные, а потенциал разделен на

Далее обсуждается, как несколько различных описаний дипольного момента среды связаны с поляризацией, входящей в уравнения Максвелла.

Среда с зарядовой и дипольной плотностями

Как описано ниже, модель для плотности поляризационного момента p ( r ) приводит к поляризационному

ограничен той же моделью. Для плавно изменяющегося распределения дипольного момента p ( r ) соответствующая плотность связанного заряда просто

В качестве первого примера, связывающего дипольный момент с поляризацией, рассмотрим среду, состоящую из непрерывной плотности заряда ρ ( r ) и непрерывного распределения дипольного момента p ( r ). Потенциал в позиции r равен:

интеграл поляризации можно преобразовать:

где объемное интегрирование распространяется только до ограничивающей поверхности и не включает эту поверхность.

Потенциал определяется общим зарядом, который, как показано выше, состоит из:

Короче говоря, плотность дипольного момента p ( r ) играет роль плотности поляризации P для этой среды. Обратите внимание, что p ( r ) имеет ненулевую дивергенцию, равную плотности связанного заряда (как моделируется в этом приближении).

Можно отметить, что этот подход может быть расширен для включения всех мультиполей: диполя, квадруполя и т. Д. Используя соотношение:

плотность поляризации оказывается равной:

Поверхностный заряд

Выше было отложено обсуждение первого члена в выражении для потенциала, обусловленного диполями. Интегрирование расходимости приводит к поверхностному заряду. Рисунок справа дает интуитивное представление о том, почему возникает поверхностный заряд. На рисунке показан однородный массив идентичных диполей между двумя поверхностями. Внутри головы и хвосты диполей смежны и сокращаются. Однако на ограничивающих поверхностях отмены не происходит. Вместо этого на одной поверхности головки диполя создают положительный поверхностный заряд, а на противоположной поверхности хвосты диполя создают отрицательный поверхностный заряд. Эти два противоположных поверхностных заряда создают чистое электрическое поле в направлении, противоположном направлению диполей.

Этой идее придается математическая форма с использованием приведенного выше потенциального выражения. Если не брать в расчет бесплатную оплату, есть вероятность:

Используя теорему о дивергенции, член дивергенции превращается в поверхностный интеграл:

Если ограничивающая поверхность является сферой, а точка наблюдения находится в центре этой сферы, интегрирование по поверхности сферы равно нулю: положительный и отрицательный вклады поверхностного заряда в потенциал сокращаются. Однако, если точка наблюдения смещена от центра, может возникнуть чистый потенциал (в зависимости от ситуации), потому что положительные и отрицательные заряды находятся на разных расстояниях от точки наблюдения. Поле, обусловленное поверхностным зарядом, равно:

который в центре сферической ограничивающей поверхности не равен нулю ( поля отрицательных и положительных зарядов на противоположных сторонах центра складываются, потому что оба поля указывают одинаково), а вместо этого:

В частности, если ввести электрическую восприимчивость через приближение:

где E в этом случае и в дальнейшем представляет внешнее поле, индуцирующее поляризацию.

Всякий раз, когда χ ( r ) используется для моделирования скачка ступеньки на границе между двумя областями, ступенька создает слой поверхностного заряда. Например, интегрирование по нормали к ограничивающей поверхности от точки внутри одной поверхности до другой точки снаружи:

обязательно включает вклад поверхностного заряда.

Физически более реалистичное моделирование p ( r ) привело бы к быстрому падению плотности дипольного момента, но плавно до нуля на границе ограничивающей области, вместо того, чтобы делать внезапный шаг к нулевой плотности. Тогда поверхностный заряд не будет концентрироваться на бесконечно тонкой поверхности, а вместо этого, будучи дивергенцией плавно изменяющейся плотности дипольного момента, будет распределяться по тонкому, но конечному переходному слою.

Диэлектрическая сфера в однородном внешнем электрическом поле

Приведенные выше общие замечания о поверхностном заряде конкретизируются на примере диэлектрического шара в однородном электрическом поле. Обнаружено, что сфера принимает поверхностный заряд, связанный с дипольным моментом ее внутренней части.

а внутри сферы потенциал удовлетворяет уравнению Лапласа. Пропуская некоторые детали, решение внутри сферы таково:

находясь вне сферы:

Как следствие, потенциал:

который является потенциалом из-за приложенного поля и, кроме того, диполя в направлении приложенного поля (направление z ) дипольного момента:

или на единицу объема:

ведущее к полю внутри сферы:

Этот пример линейного диэлектрика показывает, что рассмотрение диэлектрической проницаемости эквивалентно модели однородного дипольного момента и приводит к нулевому заряду везде, кроме поверхностного заряда на границе сферы.

Общие СМИ

Если наблюдение ограничено областями, достаточно удаленными от системы зарядов, можно сделать мультипольное разложение точной плотности поляризации. При усечении этого разложения (например, с сохранением только дипольных членов или только дипольных и квадрупольных членов и т. Д. ) Результаты предыдущего раздела восстанавливаются. В частности, усекая расширение на дипольном члене, результат неотличим от плотности поляризации, создаваемой однородным дипольным моментом, ограниченным областью заряда. Для точности этого дипольного приближения, как показано в предыдущем разделе, плотность дипольного момента p ( r ) (которая включает не только p, но и местоположение p ) служит P ( r ).

Электрические дипольные моменты элементарных частиц

Дипольные моменты молекул

Дипольные моменты можно найти в обычных молекулах, таких как вода, а также в биомолекулах, таких как белки.

ϵ знак равно 1 + k ⟨ M Tot 2 ⟩ <\ displaystyle \ epsilon = 1 + k \ left \ langle <\ mathcal > _ <\ text > ^ <2>\ right \ rangle>

Следовательно, в диэлектрическую проницаемость (и проводимость) входят оба члена. Этот подход можно обобщить для вычисления частотно-зависимой диэлектрической функции.

Источник